2021牛客暑期多校训练营1 B.Ball Dropping

最新推荐文章于 2024-08-26 21:45:03 发布

原创最新推荐文章于 2024-08-26 21:45:03 发布 · 165 阅读

0 ·

CC 4.0 BY-SA版权

笔记专栏收录该内容

5 篇文章

订阅专栏

本文探讨了一个高中数学问题，通过构建几何模型来判断一个标准球体下落时是否会卡在一个空心等腰梯形内部。利用相似三角形原理计算关键距离，进而得出球体是否会被卡住。

A standard sphere ball is falling in the air, and the center of the sphere is exactly on the centerline of an empty isosceles trapezoidal. The trapezoid is hanging horizontally under the sphere.
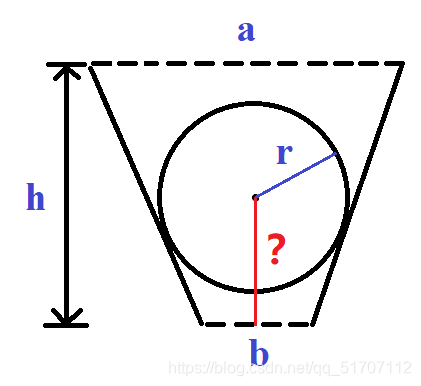
在这里插入图片描述
Please determine whether the ball will get stuck in the trapezoid or drop past the trapezoid.

思路：高中数学题，补成三角形，用相似三角形做。

代码：

#include<bits/stdc++.h>
using namespace std;
int main()
{
	double r,a,b,h;
	cin>>r>>a>>b>>h;
	double h1;//b中点到三角形顶点的距离
	h1=(b/(a-b))*h;
	double H;//等腰三角形的高
	H=(a/(a-b))*h;
	double l;//小等腰三角形的斜边
	l=H*r/(a/2);
	double h0=sqrt(r*r+l*l);//球被卡住时圆心距离三角形顶点的距离
	if(h0<=h1){
		cout<<"Drop"<<endl;
	}
	else{
		cout<<"Stuck"<<endl;
		printf("%.10lf\n",h0-h1);
	}
	return 0;
}