数据结构期末总结

数据结构

题型	题数	分值
选择	10	20
填空	10	20
判断	10	20
综合应用	4	20
算法	2	20

第一章 绪论

逻辑结构：

• 集合结构 仅属同一集合
• 线性结构 一对一
• 树结构 一对多
• 图结构 多对多 、

物理结构：

亦称存储结构，是数据的逻辑结构在计算机存储器内的表示（或映像）。它依赖于计算机。

算法的五个基本特性：

• 输入：一个算法有零个或多个输入。
• 输出 ：一个算法有一个或多个输出。
• 有穷性：一个算法必须总是在执行有穷步之后结束，且每一步都在有穷时间内完成。
• 确定性：算法中的每一条指令必须有确切的含义，在任何条件下，只有唯一的一条执行路径，即对于相同的输入只能得到相同的输出。
• 可行性：算法描述的操作可以通过已经实现的基本操作执行有限次来实现。

算法设计的要求：

• 正确性
• 可读性
• 健壮性
• 高效性

第二章 线性表

存储结构 比较项目	顺序表	链表
存储空间	预先分配，会导致空间闲置或溢出现象	动态分配，不会出现存储空间闲置或溢出现象
存储密度	不用为表示结点间的逻辑关系而增加额外的存储开销，存储密度等于1	需要借助指针来体现元素间的逻辑关系，存储密度小于1
存取元素	随机存取，按位置访问元素的时间复杂度为O(1)	顺序存取，按位置访问元素时间复杂度为O(n)
插入删除	平均移动约表中一半元素，时间复杂度为O(n),插入一个元素需要平均移动**$\frac{n}{2}$个元素，删除一个元素需要平均移动$\frac{n-1}{2}$**个元素	不需移动元素，确定插入、删除位置后，时间复杂度为O(1)
适用情况	① 表长变化不大，且能事先确定变化的范围 ② 很少进行插入或删除操作，经常按元素位置序号访问数据元素	① 长度变化较大 ② 频繁进行插入或删除操作

第三章 栈和队列

栈：先进后出

队列：先进先出

• 栈满 S.top-S.base==S.stacksize
• 栈空 base == top
• 循环入队： sq[rear]=x; rear=(rear+1)%M
• 循环出队：x=sq[front]; front=(front+1)%M
• 循环队列满 (rear+1)% M==front
• 循环队列空 front==rear

第四章 串、数组和广义表

第五章 树和二叉树

二叉树性质

• 在二叉树的第i层上至多有2^i-1个结点

• 第i层上至少有 1 个结点

• 深度为k的二叉树至多有2^K-1个结点

• 深度为k的二叉树至少有 k 个结点

• 对于任何一棵二叉树T，如果其叶子结点数为n0，度为2的结点数为n2，则n0=n2+1

完全二叉树

树与二叉树之间的转换

树转换为二叉树

将二叉树转换成树

森林转为二叉树

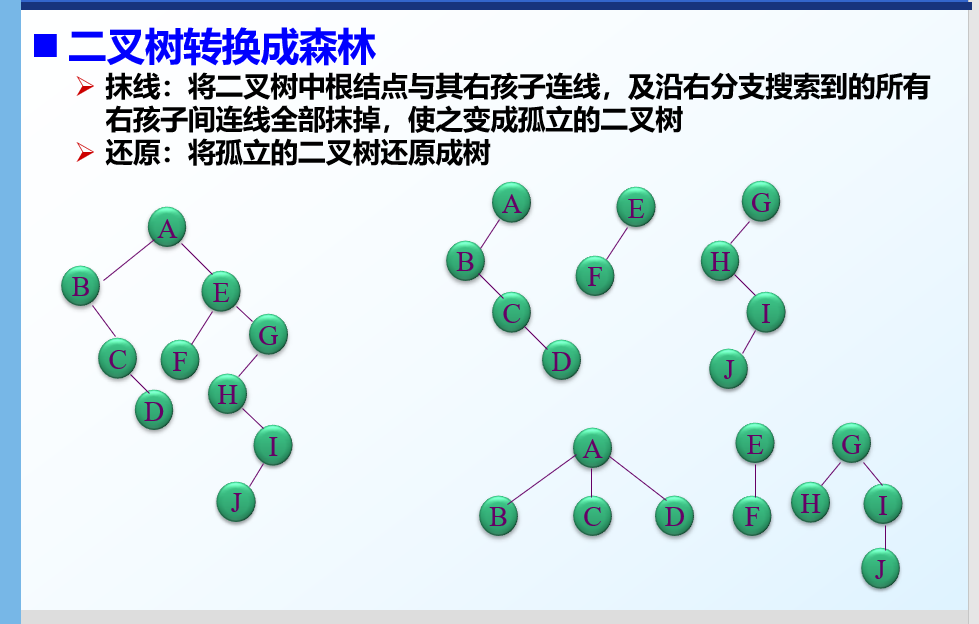
二叉树转换为森林

哈夫曼树 哈夫曼编码

第六章 图

最小生成树

Kruskal（克鲁斯卡尔）算法（不能画圈）

• 归并边，适于稀疏网
• 时间复杂度：O(eloge)
• 存储表示: 邻接表

Prim（普里姆）算法 (画圈)

• 归并顶点，与边数无关，适于稠密网
• 时间复杂度：O(n²)
• 存储表示: 邻接矩阵

算法名	普里姆算法	克鲁斯卡尔算法
时间复杂度	O(n2)	O(eloge)
适应范围	稠密图	稀疏图

最短路径

Dijkstra算法思想
先找出从源点v0到各终点vk的直达路径（v0,vk），即通过一条弧到达的路径。
从这些路径中找出一条长度最短的路径（v0,u）,然后对其余各条路径进行适当调整：
若在图中存在弧（u,vk），且（v0,u）+（u,vk）<（v0,vk）,则以路径（v0,u,vk）代替（v0,vk）。
在调整后的各条路径中，再找长度最短的路径，依此类推

关键路径

• 关键路径长度是整个工程所需的最短工期

事件v_j的最早发生时间Ve(j)

事件v_i的最迟发生时间Vl(i)

活动a_s的最早开始时间e(s)

活动a_s的最迟开始时间l(s)

例题

第七章 查找

查找名称	最好情况	最坏情况	平均情况
顺序查找	O(1)	O(n)	$\frac{n+1}{2}$(平均查找次数)
折半查找			O(logn)
分块查找			O(logn)
二叉排序树查找			O(logn)

分块查找（索引顺序查找）

• 当对一个线性表R[60]进行索引顺序查找（分块查找）时，若共分成了10个子表，每个子表有6个表项。假定对索引表和数据子表都采用顺序查找，则查找每一个表项的平均查找长度为( 9 ) 。

平衡二叉树

• 性质：任一结点的平衡因子只能取：-1、0 或 1；如果树中某个结点的平衡因子的绝对值大于1，则这棵二叉树就失去平衡，不再是AVL树

LL型（右旋转）

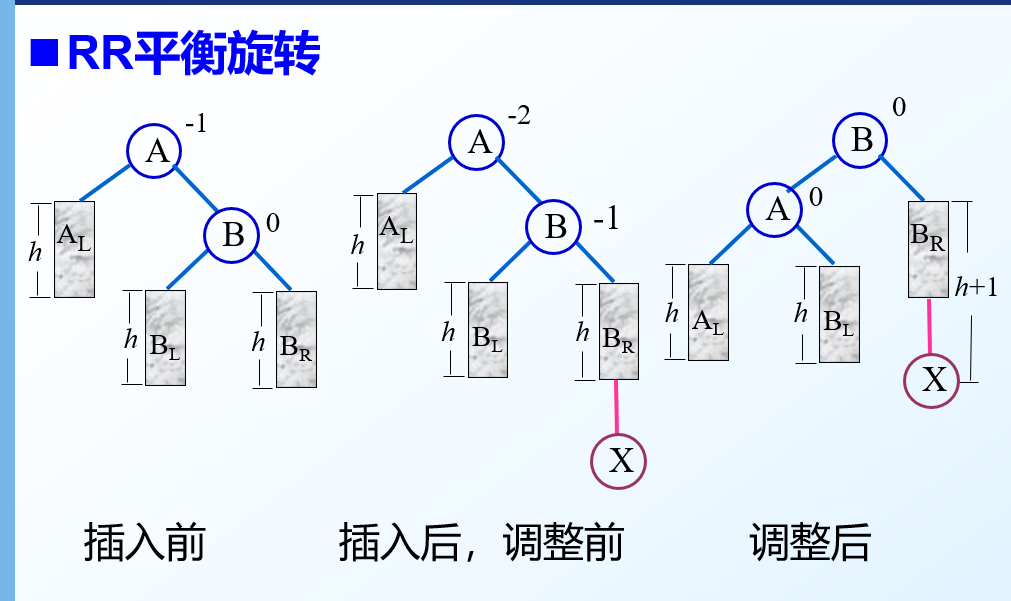
RR型（左旋转）

LR型

• 先进行一次左旋转变成LL型，再进行一次右旋转

RL型

• 先进行一次右旋转变成RR型，再进行一次左旋转

散列表

散列函数构造方法：

• 数字分析法
• 平方取中法
• 折叠法
• 除留余数法

处理冲突

处理冲突的方法：

• 开放定址法
• 再散列法
• 链地址法
• 建立一个公共溢出区

开放定址法：
方法：当冲突发生时，形成一个探查序列；沿此序列逐个地址探查，直到找到一个空位置（开放的地址），将发生冲突的记录放到该地址中，即Hi=(H(key)+di)MOD m, i=1,2,…,k(k <=m-1)
H(key)—散列函数,m —散列表表长,di —增量序列
分类
线性探测再散列： di =1,2,3,…,m-1
二次探测再散列： di =1²,-1²,2²,-2²,3²,…,±k²(k<=m/2)
伪随机探测再散列： di =伪随机数序列

再散列法：

方法：构造若干个散列函数，当发生冲突时，计算下一个散列地址，即：Hi=RHi(key) i=1,2,…,k
RHi—不同的散列函数
特点：计算时间增加

链地址法：
方法：将所有关键字为同义词的记录存储在一个单链表中，并用一维数组存放头指针

建立一个公共溢出区：
除设立散列基本表外，另设立一个溢出向量表。所有关键字和基本表中关键字为同义词的记录，不管它们由散列函数得到的地址是什么，一旦发生冲突，都填入溢出表。

第八章 排序