44_变分自编码器VAE详解

 简介

变分自编码器（Variational Autoencoder, VAE）是一种基于深度学习的生成模型，它结合了传统的自动编码器（Autoencoder, AE）和概率图模型的思想。VAE旨在学习数据的概率分布，从而能够生成与训练数据具有相似特性的新样本。

自动编码器简介
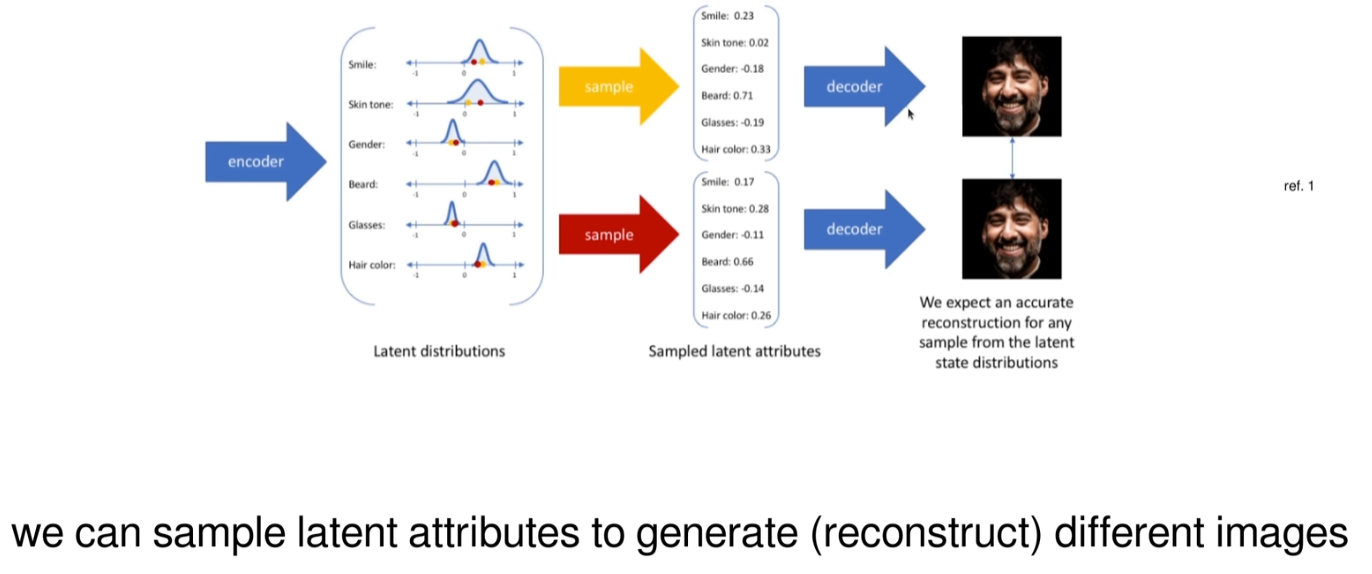
在了解变分自编码器之前，先简单介绍自动编码器。自动编码器是一种无监督学习算法，其目的是学习一个压缩表示（编码），然后尽可能准确地重构输入数据（解码）。自动编码器通常由两部分组成：编码器（Encoder）和解码器（Decoder）。编码器将输入数据映射到一个低维空间（称为潜在空间或隐空间），解码器则尝试从这个低维表示重建原始输入。

变分自编码器的特点
变分自编码器与传统自动编码器的关键区别在于它引入了概率论中的变分推断方法。具体来说，VAE不仅试图学习如何重建输入数据，还试图学习输入数据的潜在分布。为了实现这一点，VAE对潜在变量施加了一个先验分布（通常是标准正态分布），并且通过优化一个叫做变分下界（Evidence Lower Bound, ELBO）的目标函数来确保潜在变量的分布接近这个先验分布。

应用
由于 VAE 能够学习数据的有效表示并生成新的数据样本，因此它在多个领域都有应用，包括但不限于：

图像生成
数据降维和可视化
异常检测
半监督学习
图像处理任务，如去噪、超分辨率等

ELBO

目标函数

重参数化

在 VAE 中，重参数化技巧（reparameterization trick）是实现高效训练的关键。这是因为 VAE 的损失函数包含了一个期望值，这个期望值需要对潜在变量进行积分，而直接计算这个积分通常是不可行的。因此，我们需要一种方法来近似这个期望值，同时保持梯度信息，以便能够使用基于梯度的方法（如随机梯度下降）来优化模型参数。

为什么使用重参数化技巧？
使梯度估计成为可能：由于 ϵ 是独立于模型参数的，所以当我们在 μ 和 σ 上应用梯度时，不会影响到 ϵ 的分布。这允许我们直接计算损失函数相对于 μ 和 σ 的梯度，而不需要对 z 进行显式的积分。
提高采样效率：相比于其他采样方法，比如马尔科夫链蒙特卡洛方法（MCMC），重参数化技巧通常能更快速地获得样本，并且这些样本之间的相关性更低，有助于更快地收敛。
简化训练过程：重参数化技巧让 VAE 的训练变得像训练普通的神经网络一样简单，因为我们可以使用标准的优化技术来进行训练。

损失函数

隐空间可视化

1. 初始阶段
随机初始化：在训练开始时，VAE 的权重是随机初始化的，因此隐空间中的潜在变量 𝑧 分布也是随机的。此时，模型对数据的理解非常有限。
先验分布：通常我们会假设潜在变量 z 遵循一个简单的先验分布，比如标准正态分布 。这个假设有助于保持隐空间的结构化，并使得不同样本之间的潜在表示更加平滑和连续。
2. 中期训练
后验分布逼近：随着训练的进行，编码器网络会学习将输入数据映射到隐空间中，同时解码器网络会尝试从隐空间重构原始输入。理想情况下，编码器输出的分布（即后验分布） 应该尽可能接近我们所设定的先验分布 p(z)。
信息压缩与表达：在这个阶段，VAE 学习如何有效地压缩输入数据到隐空间，并从中提取出有意义的信息。隐空间中的每个维度可能开始对应于某些数据特征或模式。
隐空间的结构化：由于 KL 散度项的作用，隐空间变得越来越有组织，相似的数据点在隐空间中的位置也会更接近。这不仅有助于提高重构质量，而且也使得通过采样隐空间中的点来生成新的、合理的数据样本成为可能。
3. 后期训练
稳定化：当训练达到一定程度后，隐空间的分布趋于稳定，不再发生显著变化。此时，编码器已经学会了如何将输入映射到符合先验分布的隐空间区域，而解码器则能很好地根据这些潜在向量重建原始输入。
泛化能力：良好的隐空间结构意味着模型具有更好的泛化能力。即使对于未曾见过的数据，VAE 也能通过其学到的映射关系找到合适的潜在表示，并准确地重构或生成新样本。
4. 隐空间的特性
连续性和平滑性：理想的隐空间是连续和平滑的，这意味着相邻的数据点在隐空间中的表示也应该相近。这种特性对于插值和其他形式的数据探索非常重要。
稀疏性和效率：尽管隐空间可以很大，但有效的 VAE 模型通常会使大部分信息集中在较少的几个维度上，其余维度则几乎不携带信息或者携带很少的信息。这样既提高了计算效率，又简化了对隐空间的理解。
可解释性：在一些情况下，隐空间的不同维度可能会对应于输入数据的具体属性或特征（如图像的颜色、形状等），这为理解模型的工作原理提供了帮助。