顺序（线性）查找

1.顺序查找（线性查找）：从线性表的一端向另一端逐个将记录与给定值进行比较，若相等，则查找成功，给出该记录在表中的位置；若整个表检测完仍未找到与给定值相等的记录，则查找失败，给出失败信息

#include <iostream>

using namespace std;
int SeqSearch(int a[],int n,int k){
    int i=n;
    while(i>=0&&a[i]!=k){
        i--;
    }
    return i;
}
int main()
{
    int a[9]={0,22,4,8,12,36,24,45,54};
    int k,y;
    cout<<"请输入要查询的数字："<<endl;
    cin>>k;
    y=SeqSearch(a,8,k);//注意数组下标越界问题
    if(y!=-1){
        cout<<"查询数字在数组中的下标是"<<y<<endl;
    }else{
        cout<<"查找失败"<<endl;
    }
    return 0;
}

2.顺序查找的改进：设置“哨兵”——待查值，放在查找方向的尽头处，免去了每一次比较后都要判断查找位置是否越界

#include <iostream>

using namespace std;
int SeqSearch(int a[],int n,int k){
    int i=n;
    a[0]=k;
    while(a[i]!=k){
        i--;
    }
    return i;
}
int main()
{
    int a[9]={0,22,4,8,12,36,24,45,54};
    int k,y;
    cout<<"请输入要查询的数字："<<endl;
    cin>>k;
    y=SeqSearch(a,8,k);//注意数组下标越界问题
    if(y){//if(y!=0)
        cout<<"查询数字在数组中的下标是"<<y<<endl;
    }else{
        cout<<"查找失败"<<endl;
    }
    return 0;
}

3.顺序查找的性能

查找成功：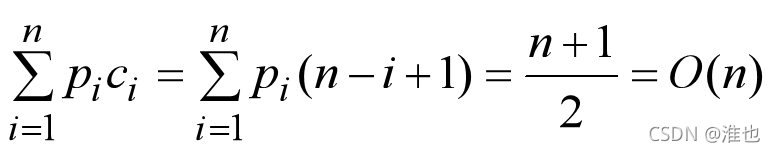

 查找失败：

 4.顺序查找的优缺点

缺点：查找效率较低

优点：算法简单而且使用面广

• 对表中记录的存储没有任何要求，顺序存储和链接存储均可
• 对表中记录的有序性也没有要求，无论记录是否按关键码有序均可