P4779 【模板】单源最短路径（标准版） 题解

P4779 【模板】单源最短路径（标准版） 题解

本文使用方法：

图的存储结构：链式前向星
涉及优化：堆优化
算法：Dijkstra算法
P4779：传送门

题目背景
2018 年 7 月 19 日，某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。

然后呢？

100→60；

Ag→Cu；

最终，他因此没能与理想的大学达成契约。

小 F 衷心祝愿大家不再重蹈覆辙。

题目描述
给定n个点，m 条有向边的非负权图，请你计算从 s 出发，到每个点的距离。

数据保证你能从 s 出发到任意点。

输入格式
第一行为三个正整数 n, m, s。 第二行起 m 行，每行三个非负整数 ui, vi, wi ，表示从ui到vi有一条权值为wi的有向边。

输出格式
输出一行 n 个空格分隔的非负整数，表示 s到每个点的距离。

输入
4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出
0 2 4 3

下面是链式前向星使用例程，包含了加边和遍历两种算法

#include<iostream>
using namespace std;
//结构体
const int maxn=10000;
struct edge{int nex,to,w;}e[maxn];
int h[maxn],tot;
void add_edge(int u,int v,int w){
    e[++tot]=edge{h[u],v,w};
    h[u]=tot;
}

int main()
{
    int a,b,w;
    int n,m;
    cin>>n>>m;
    while(m--)
    {
        cin>>a>>b>>w;
        add_edge(a,b,w);
    }
   // x;//出发点
    //e[i].to; // 连接到的点
    //e[i].w; // 边权
    for(int x=1;x<=n;x++)
    {
cout<<x<<endl;
    for(int i = h[x]; i; i = e[i].nex) {
    cout<<x<<" "<<e[i].to<<" "<<e[i].w<<endl;
    }
    cout<<endl;

}
return 0;
}

帮助理解的输入输出：
输入：
4 6
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4
输出：
输出的是出发点，和以这个点为起点从下到上的边集合

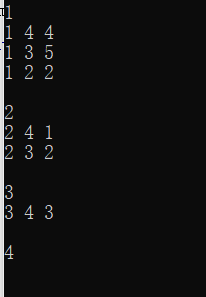
这个是ac代码

#include<iostream>
#include<algorithm>
#include<queue>
#include<string.h>
using namespace std;
const int maxn=2e5+7;
const int INF=1e9;
struct edge{int nex,to,w;};
edge e[maxn];
int h[maxn*2],tot;
int dis[maxn];
bool pd[maxn*2];

struct node{
int p;//目标点
int dist;//现距离
bool operator <(const node& x)const{
return x.dist<dist;//最小堆
}
};
priority_queue<node>q;
/* 核心函数1：加边*/
void add_edge(int u,int v,int w)
{
    e[++tot]=edge{h[u],v,w};
    h[u]=tot;
}
/* 核心函数2：Dijkstra*/
void Dijkstra(int s)
{
    dis[s]=0;
    q.push(node{s,0});
    while(!q.empty()) //重复直至空
    {
        node now,next;
        //第一步：挑选最短且没有被扩展的点
        now=q.top();q.pop();
        if(pd[now.p])continue;

        //第二步：记录已扩展
        pd[now.p]=true;

        //第三步：根据该点更新dist
        for(int i=h[now.p];i;i=e[i].nex)
        {
            int y=e[i].to;
            if(dis[y]>(long long)dis[now.p]+e[i].w)
            {
                dis[y]=dis[now.p]+e[i].w;
                if(!pd[y])  //第四步：未被扩展则加入
                {
                    q.push(node{y,dis[y]});
                }
            }
        }
    }
}
int main()
{
    memset(pd,false,sizeof(pd));
    int n,m,s;
    cin>>n>>m>>s;

    while(m--)
    {
         int u,v,w;
        cin>>u>>v>>w;
        add_edge(u,v,w);
    }
    fill(dis+1,dis+1+n,INF);
    Dijkstra(s);
    for(int i=1;i<n;i++)cout<<dis[i]<<" ";
    cout<<dis[n]<<endl;
    return 0;
}