自回归图像学习——FSQ RQ-VAE个人理解

FSQ-VAE：四舍五入让离散更简单

VQ-VAE在前面我们已经介绍过了，他的离散方法是通过最近邻搜索算法寻找码本中的最相似向量，因此VQ-VAE相当于将码本分为了K个类，然后将编码器的连续向量映射到K类中的一类。

这样的码本大小可以说是相当大的，于是就有人提出了FSQ方法做离散，想要优化VQ方法并缩小码本大小。

FSQ的思路是这样的：

1. 先将连续向量的每个值映射到 长度为L的数组中，具体怎么映射呢？先将连续向量使用激活函数（如果后续是乘以L-1就使用sigmoid，如果是乘以L/2就使用tanh函数）映射到 [0, 1]或[-1, 1]之间，然后乘以预先定义的超参数 L-1 或L/2就将连续变量映射到了 [0, L-1]或[-L/2, L/2]中。
2. 将值转到这个范围之后进行四舍五入操作，将连续向量的实数映射为离散的整数，达到离散化的目标。

总的来说核心就是下面的式子，确实很简单

同样，四舍五入也不能直接反向传播优化，因此也是使用STE技巧，详细可以看之前的介绍。

与VQ离散化相比确实简单了很多，因为四舍五入天生具有近似的性质，因此不用特地使用loss再拟合离散向量与连续向量。

假设VQ中，一个d维的连续向量做映射需要一个分出K类的大码本，现在FSQ中，相当于没有使用码本，而是将连续向量分为d个部分，每部分有L种选择，一共可以表示种选择。简单来说就是VQ做的是多目标分类任务，FSQ做的只是四舍五入任务。

如果与VQ对齐的话，令=K，则L = 或者d = ，我们更关注的是后者。因为后者意味着可以通过增加L来减少Encoder之后连续向量的维度d，这样的话自回归模型的计算成本也会减少（但是d也不能太小，否则会损失很多图像信息），可能VQ中连续向量的维度d是三位数，FSQ中只需要一位数。

RQ-VAE：残差VAE

RQ-VAE的设计也是为了解决VQ中码本过大的缺点，个人理解RQ的思想就是迭代残差。

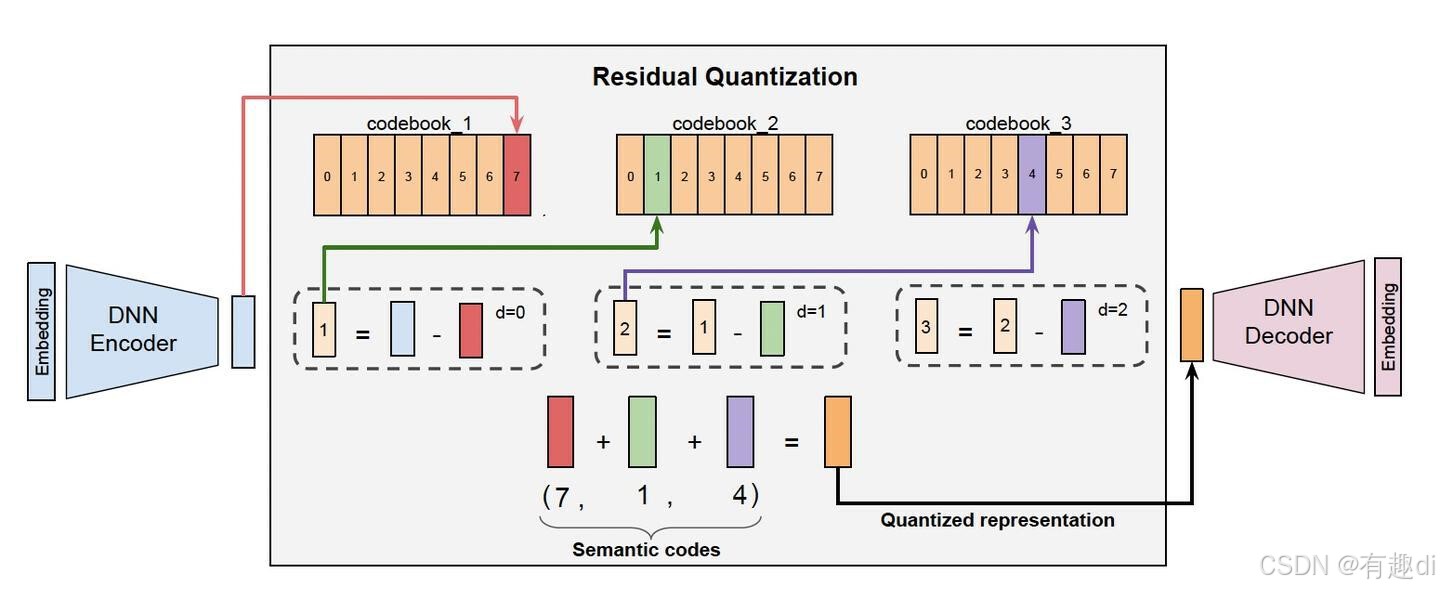可以这样理解：

1. 拿到一个连续向量x，找到与其最近邻的离散向量 e(k1)，然后两者相减得到残差
2. 这时我们再针对这个残差找 的最近邻向量 e(k2) ，两者相减得到残差
3. 重复这样的迭代，我们就可以将最终残差尽可能的缩小
4. 最后，将每次的减数部分相加，即 e(k1)+e(k2)+...+e(kn)就得到了无限趋近于原始连续向量的离散向量

因此，RQ-VAE中的码本是分层设计的，也就是说有多层码本，每层的码本大小相同。这样的多层码本设计可以显著减小单层码本的大小，对于减少连续向量的维度d来说还是很有用的。

RQ的图像重建用的是Transformer，在此没有往下看，只关注了如何离散化的操作。为什么看RQ-VAE呢，今年字节的一篇自回归模型好像就是基于这种离散化的方法。

以上就是我个人对FSQ和RQ-VAE的非常简单理解，对于更深入的理解欢迎讨论！