二叉树算法

一： 二叉树基础

1.1 二叉种类

1.1.1 满二叉树

满二叉树：就是所有节点要么为0要么为2

1.1.2 完全二叉树

完全二叉树的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层（h从1开始），则该层包含 1~ 2^(h-1) 个节点。

因为，需要顺序，先左后右

1.1.3 二叉搜索树

二叉搜索树是一个有序树。
若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；
若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；
它的左、右子树也分别为二叉排序树

1.1.4 平衡二叉搜索树

平衡二叉搜索树：又被称为AVL（Adelson-Velsky and Landis）树，且具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

1.2 二叉树存储方式

二叉树可以链式存储，也可以顺序存储。
链式存储：指针

顺序存储：数组

数组存储：如果父节点的数组下标是 i，那么它的左孩子就是 i * 2 + 1，右孩子就是 i * 2 + 2。

1.3 二叉树的遍历方式

1.3.1 深度优先遍历

前序遍历：中左右
中序遍历：左中右
后序遍历：左右中

1.3.2 广度优先遍历

层次遍历（主要是通过队列实现，一层一层遍历二叉树）

1.4 二叉树的定义

我们主要以链表方式存储二叉树

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

和链表的定义基本一致。

1.5 前中后序的递归遍历算法总结

前序遍历

    void traversal(TreeNode* cur, vector<int>& vec) {
        if (cur == NULL) return;
        //前序代码位置
        vec.push_back(cur->val);    // 中
        traversal(cur->left, vec);  // 左
        traversal(cur->right, vec); // 右
    }

中序遍历

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    //中序代码位置
    vec.push_back(cur->val);    // 中
    traversal(cur->right, vec); // 右
}

后续遍历
这道题为力扣145二叉树的后序遍历

	vector<int>res;
   vector<int> postorderTraversal(TreeNode* root) {
        if(root == nullptr)
        {
            return res;
        }
        postorderTraversal(root->left); // 左
        postorderTraversal(root->right); // 右
        // 后序代码位置
        res.push_back(root->val); //中
        return res;
    }

下面这个如同上文的模板一致。

void traversal(TreeNode* cur, vector<int>& vec) {
    if (cur == NULL) return;
    traversal(cur->left, vec);  // 左
    traversal(cur->right, vec); // 右
    //后续遍历位置
    vec.push_back(cur->val);    // 中
}

1.6 前中后序的迭代遍历

遍历思路，以前序为例：
前序是左中右，每次先处理中间节点，然后将根节点放入栈中，再将右孩子放入栈中，再放入左孩子（因为栈，先进后出，所以，先放右左，出就是 左右，即为前序遍历顺序，中左右）。
代码如下：
前序遍历：

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();                       // 中
            st.pop();
            result.push_back(node->val);
            if (node->right) st.push(node->right);           // 右（空节点不入栈）
            if (node->left) st.push(node->left);             // 左（空节点不入栈）
        }
        return result;
    }
};

中序遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) {
            if (cur != NULL) { // 指针来访问节点，访问到最底层
                st.push(cur); // 将访问的节点放进栈
                cur = cur->left;                // 左
            } else {
                cur = st.top(); // 从栈里弹出的数据，就是要处理的数据（放进result数组里的数据）
                st.pop();
                result.push_back(cur->val);     // 中
                cur = cur->right;               // 右
            }
        }
        return result;
    }
};

后序遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        vector<int> result;
        if (root == NULL) return result;
        st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);
            if (node->left) st.push(node->left); // 相对于前序遍历，这更改一下入栈顺序 （空节点不入栈）
            if (node->right) st.push(node->right); // 空节点不入栈
        }
        reverse(result.begin(), result.end()); // 将结果反转之后就是左右中的顺序了
        return result;
    }
};

1.7 前中后序的统一迭代法

对于需要处理的节点，我们做个标记，比如将处理节点放入栈中，我们就放个空指针做标记。比如输出，我们遇到空指针，我们就知道下一个节点就是我们需要处理的。如图：

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop(); // 将该节点弹出，避免重复操作，下面再将右中左节点添加到栈中
                if (node->right) st.push(node->right);  // 添加右节点（空节点不入栈）

                st.push(node);                          // 添加中节点
                st.push(NULL); // 中节点访问过，但是还没有处理，加入空节点做为标记。

                if (node->left) st.push(node->left);    // 添加左节点（空节点不入栈）
            } else { // 只有遇到空节点的时候，才将下一个节点放进结果集
                st.pop();           // 将空节点弹出
                node = st.top();    // 重新取出栈中元素
                st.pop();
                result.push_back(node->val); // 加入到结果集
            }
        }
        return result;
    }
};

前序遍历

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左
                st.push(node);                          // 中
                st.push(NULL);
            } else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

后序遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if (root != NULL) st.push(root);
        while (!st.empty()) {
            TreeNode* node = st.top();
            if (node != NULL) {
                st.pop();
                st.push(node);                          // 中
                st.push(NULL);

                if (node->right) st.push(node->right);  // 右
                if (node->left) st.push(node->left);    // 左

            } else {
                st.pop();
                node = st.top();
                st.pop();
                result.push_back(node->val);
            }
        }
        return result;
    }
};

1.8 层序遍历

层序，就是通过队列先进先出，一层一层遍历

迭代框架：

class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        queue<TreeNode*> que;
        if (root != NULL) que.push(root);
        vector<vector<int>> result;
        while (!que.empty()) {
            int size = que.size();
            vector<int> vec;
            // 这里一定要使用固定大小size，不要使用que.size()，因为que.size是不断变化的
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                vec.push_back(node->val);
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
            result.push_back(vec);
        }
        return result;
    }
};

递归框架：

# 递归法
class Solution {
public:
    void order(TreeNode* cur, vector<vector<int>>& result, int depth)
    {
        if (cur == nullptr) return;
        if (result.size() == depth) result.push_back(vector<int>());
        result[depth].push_back(cur->val);
        order(cur->left, result, depth + 1);
        order(cur->right, result, depth + 1);
    }
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> result;
        int depth = 0;
        order(root, result, depth);
        return result;
    }
};

二：二叉树总纲领

二叉树解题思维模式：
1.遍历
2.递归

2.1 深入理解前中后序

二叉树遍历框架：

void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // 前序位置
    traverse(root->left);
    // 中序位置
    traverse(root->right);
    // 后序位置
}

此框架和我们之前将解过的遍历数组和链表没有本质区别：

//迭代遍历数组
void traverse(vector<int>& arr) {
    for (int i = 0; i < arr.size(); i++) {

    }
}

//递归遍历数组
void traverse(vector<int>& arr, int i) {
    if (i == arr.size()) {
        return;
    }
    //前序位置
    traverse(arr, i + 1);
    //后序位置
}

//迭代遍历单链表
void traverse(ListNode* head) {
    for (ListNode* p = head; p != nullptr; p = p -> next) {

    }
}

//递归遍历单链表
void traverse(ListNode* head) {
    if (head == nullptr) {
        return;
    }
    //前序位置
    traverse(head -> next);
    //后序位置
}

由此代码可以清晰明白，只要递归形式的遍历，都可以存在前序位置和后序位置，分别再递归之前和递归之后。
所以总结一下：
所谓前序位置，就是刚进入一个节点（元素）的时候，后序位置就是即将离开一个节点（元素）的时候

所以：前中后序就是遍历二叉树过程中处理每个节点的三个特殊时间点：

前序位置的代码在刚刚进入一个二叉树节点的时候执行；
后序位置的代码在将要离开一个二叉树节点的时候执行；
中序位置的代码在一个二叉树节点左子树都遍历完，即将开始遍历右子树的时候执行。

前序位置属于自顶向下，后序是自底向上

总结：
二叉树的问题，就是你自己根据前中后序位置注入自己的代码逻辑，只需要思考每个节点应该做什么，其他的直接抛给遍历框架。

2.2两种解题思路

二叉树的递归有两种思路：
1 .遍历二叉树：回溯算法框架
2 .分解问题：动态规划框架
力扣第 104 题「二叉树的最大深度」
遍历代码：

// 记录最大深度
int res = 0;
// 记录遍历到的节点的深度
int depth = 0;

// 主函数
int maxDepth(TreeNode* root) {
    traverse(root);
    return res;
}

// 二叉树遍历框架
void traverse(TreeNode* root) {
    if (root == NULL) {
        return;
    }
    // 前序位置
    depth++;
    if (root->left == NULL && root->right == NULL) {
        // 到达叶子节点，更新最大深度
        res = max(res, depth);
    }
    traverse(root->left);
    traverse(root->right);
    // 后序位置
    depth--;
}

为什么需要 depth-- ？，前面阐述过，前序是进入节点位置，后序是离开节点位置，depth 记录当前递归到的节点深度，你把 traverse 理解成在二叉树上游走的一个指针，所以当然要这样维护。
至于对 res 的更新，你放到前中后序位置都可以，只要保证在进入节点之后，离开节点之前（即 depth 自增之后，自减之前）就行了。

分解问题代码：

// 定义：输入根节点，返回这棵二叉树的最大深度
int maxDepth(TreeNode* root) {
	if (root == nullptr) {
		return 0;
	}
	// 利用定义，计算左右子树的最大深度
	int leftMax = maxDepth(root->left);
	int rightMax = maxDepth(root->right);
	// 整棵树的最大深度等于左右子树的最大深度取最大值，
    // 然后再加上根节点自己
	int res = max(leftMax, rightMax) + 1;

	return res;
}

就是将该二叉树，分解为左右子树深度问题。

2.2.1 前序遍历

最常规的遍历写法：

vector<int> res;

// 前序遍历结果
vector<int> preorderTraverse(TreeNode* root) {
    traverse(root);
    return res;
}
// 二叉树遍历函数
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }
    // 前序位置
    res.push_back(root->val);
    traverse(root->left);
    traverse(root->right);
}

上文讲解过分解问题，如何直接用分解思路计算前序遍历结果？

// 定义：输入一棵二叉树的根节点，返回这棵树的前序遍历结果
vector<int> preorderTraverse(TreeNode* root) {
    vector<int> res;
    if (root == nullptr) {
        return res;
    }
    // 前序遍历的结果，root->val 在第一个
    res.push_back(root->val);
    // 利用函数定义，后面接着左子树的前序遍历结果
    vector<int> leftRes = preorderTraverse(root->left);
    res.insert(res.end(), leftRes.begin(), leftRes.end());
    // 利用函数定义，最后接着右子树的前序遍历结果
    vector<int> rightRes = preorderTraverse(root->right);
    res.insert(res.end(), rightRes.begin(), rightRes.end());

    return res;
}

总结：
1、**是否可以通过遍历一遍二叉树得到答案？**如果可以，用一个 traverse 函数配合外部变量来实现。
2、是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。
3、无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

2.2.2 后序位置的特殊之处

查看下图，和我们上文阐述过，前序自顶向下，后序自底向上。
前序：只能获取父节点传递的数据。
后序：不仅可以获取父节点传递数据，也可以获取子树同ing过函数返回值传递的数据。

所以；看下面两个问题。
1 .如果把根节点看作第一层，如何打印每个节点所在层数？

// 二叉树遍历函数
void traverse(TreeNode* root, int level) {
    if (root == NULL) {
        return;
    }
    // 前序位置
    printf("节点 %s 在第 %d 层", root, level);
    traverse(root->left, level + 1);
    traverse(root->right, level + 1);
}

// 这样调用
traverse(root, 1);

2 .如何打印每个节点的左右子树各有多少个节点？

// 定义：输入一棵二叉树，返回这棵二叉树的节点总数
int count(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    int leftCount = count(root->left);
    int rightCount = count(root->right);
    // 后序位置
    printf("节点 %s 的左子树有 %d 个节点，右子树有 %d 个节点",
            root->val, leftCount, rightCount);

    return leftCount + rightCount + 1;
}

这两个问题有什么区别呢？：一个节点在第几层，从根节点遍历就直接可以输出。而以一个节点为根的整棵树有多少个节点，你就得遍历完整个树才能清楚，然后递归返回值得到答案。
所以：什么时候可以用后序？
当你发现题目和子树有关，就可以通过后序位置获得返回值

2.2.2.1 力扣第 543 题「二叉树的直径」

class Solution {
public:
    //int depth = 0;

    int diameterOfBinaryTree(TreeNode* root) {
        int res = 0;
        depth(root,res);
        return res;
    }

    int depth(TreeNode* root,int &res)
    {
        if(root == nullptr)
        {
            return 0;
        }
        int leftdepth = depth(root->left,res);
        int rightdepth = depth(root->right,res);
        //返回该节点，以该节点为根节点的最大长度
        res = max(res,leftdepth+rightdepth);
		//返回左右子树最大深度
        return max(leftdepth,rightdepth)+1;
    }
};

2.3 层序遍历

层序遍历也属于迭代遍历，下面为层序遍历代码框架：

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode* root) {
    if (root == nullptr) return;
    queue<TreeNode*> q;
    q.push(root);

    // 从上到下遍历二叉树的每一层
    while (!q.empty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.front();
            q.pop();
            // 将下一层节点放入队列
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
    }
}

代码中的while循环和for循环就是从上到下，从左到右遍历啊：

也可以通过递归函数进行层序遍历：

class Solution {
public:
    vector<vector<int>> res;
    
    vector<vector<int>> levelTraversal(TreeNode* root) {
        if (root == nullptr) {
            return res;
        }
        // root 视为第 0 层
        traverse(root, 0);
        return res;
    }

    void traverse(TreeNode* root, int depth) {
        if (root == nullptr) {
            return;
        }
        // 前序位置，看看是否已经存储 depth 层的节点了
        if (res.size() <= depth) {
            // 第一次进入 depth 层
            res.push_back(vector<int>());
        }
        // 前序位置，在 depth 层添加 root 节点的值
        res[depth].push_back(root->val);
        traverse(root->left, depth + 1);
        traverse(root->right, depth + 1);
    }
};

2.4 后序问题

力扣第 652 题「寻找重复的子树」
判断重复子树问题，可以想想两个点：
1 .以此为根的二叉树（子树）是什么样？
2 .以其他节点为根的子树又是什么样？
第一个点：查看以此为根的二叉树样子，可以用到后序代码。

// 定义：输入以 root 为根的二叉树，返回这棵树的序列化字符串
string serialize(TreeNode* root) {
    // 对于空节点，可以用一个特殊字符表示
    if (root == NULL) {
        return "#";
    }
    // 将左右子树序列化成字符串
    string left = serialize(root->left);
    string right = serialize(root->right);
    /* 后序遍历代码位置 */
    // 左右子树加上自己，就是以自己为根的二叉树序列化结果
    string myself = left + "," + right + "," + to_string(root->val);
    return myself;
}

这样我们通过后序遍历思路，将二叉树进行了序列化操作。
第二个点，已经知道了自己，那么其他节点如何知晓？
借用容器，将每个节点的序列化结果放进去，饭后进行对比，就可以查询到是否有从重复的。

class Solution {
public:
    // 记录所有子树以及出现的次数
    unordered_map<string, int> subTrees;
    // 记录重复的子树根节点
    vector<TreeNode*> res;

    vector<TreeNode*> findDuplicateSubtrees(TreeNode* root) {
        serialize(root);
        return res;
    }
    string serialize(TreeNode* root)
    {
        if(root == nullptr)
        {
            return "#";
        }

        string left = serialize(root->left);
        string right = serialize(root->right);
        string myself = left + "," + right + "," + to_string(root->val); 

        int flag = subTrees[myself];
        if(flag == 1)
        {
            res.push_back(root);
        }
        subTrees[myself]++;
        return myself;
    }
};

三：二叉树思路

3.1 反转二叉树

力扣第 226 题「翻转二叉树」
1 .遍历思维解决问题

// 主函数
TreeNode* invertTree(TreeNode* root) {
    // 遍历二叉树，交换每个节点的子节点
    traverse(root);
    return root;
}

// 二叉树遍历函数
void traverse(TreeNode* root) {
    if (root == nullptr) {
        return;
    }

    /**** 前序位置 ****/
    // 每一个节点需要做的事就是交换它的左右子节点
    //TreeNode* tmp = root->left;
    //root->left = root->right;
    //root->right = tmp;
    swap(toor->left,root->right);

    // 遍历框架，去遍历左右子树的节点
    traverse(root->left);
    traverse(root->right);
    //swap(toor->left,root->right);
}

左右交换函数，前序和后序均可以。

2 .分解问题解决：

class Solution {
public:
    TreeNode* invertTree(TreeNode* root) {
        if(root == nullptr)
        {
            return nullptr;
        }
        TreeNode* left = invertTree(root->left);
        TreeNode* right = invertTree(root->right);

        root->left = right;
        root->right = left;
        return root;
    }
};

3.2 填充节点右侧指针

力扣第 116 题「填充每个二叉树节点的右侧指针」
遍历法解决：

// 主函数
Node* connect(Node* root) {
    if (root == nullptr) return nullptr;
    // 遍历「三叉树」，连接相邻节点
    traverse(root->left, root->right);
    return root;
}

// 三叉树遍历框架
void traverse(Node* node1, Node* node2) {
    if (node1 == nullptr || node2 == nullptr) {
        return;
    }
    /**** 前序位置 ****/
    // 将传入的两个节点穿起来
    node1->next = node2;
    
    // 连接相同父节点的两个子节点
    traverse(node1->left, node1->right);
    traverse(node2->left, node2->right);
    // 连接跨越父节点的两个子节点
    traverse(node1->right, node2->left);
}

当然也可以用迭代法进行遍历：

    Node* connect(Node* root) {
      queue<Node *>que;
      if(root != NULL)
      {
          que.push(root);
      }  
      while(!que.empty())
      {
          int size = que.size();
          for(int i = 0;i<size;i++)
          {
              Node *node = que.front();
              que.pop();
              if(i == (size - 1))
              {
                  node->next = NULL;
              }
              else
              {
                  node->next = que.front();
              }
              if(node->left)
              {
                  que.push(node->left);
              }
              if(node->right)
              {
                  que.push(node->right);
              }
          }
      }
      return root;
    }

3.3 将二叉树展开为链表

力扣第 114 题「将二叉树展开为链表」

// 定义：将以 root 为根的树拉平为链表
void flatten(TreeNode* root) {
    // base case
    if (root == nullptr) return;

    // 利用定义，把左右子树拉平
    flatten(root->left);
    flatten(root->right);

    /**** 后序遍历位置 ****/
    // 1、左右子树已经被拉平成一条链表
    TreeNode* left = root->left;
    TreeNode* right = root->right;

    // 2、将左子树作为右子树
    root->left = nullptr;
    root->right = left;

    // 3、将原先的右子树接到当前右子树的末端
    TreeNode* p = root;
    while (p->right != nullptr) {
        p = p->right;
    }
    p->right = right;

}

四：二叉树构造问题

二叉树的构造问题一般都是使用「分解问题」的思路：构造整棵树 = 根节点 + 构造左子树 + 构造右子树。

4.1 构造最大二叉树

力扣第 654 题「最大二叉树」
我们可以先找到最大的值当作根节点，然后数组的根节点左右分别当作左右子树。

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        if(nums.empty())
        {
            return NULL;
        }
        int max = INT_MIN;
        int index = 0;
        for(int i = 0 ;i < nums.size(); i++)
        {
            if(nums[i]>max)
            {
                max = nums[i];
                index = i;
            }
        }
        TreeNode* root = new TreeNode(max);

        if(index > 0)
        {
            vector<int> leftnums(nums.begin(),nums.begin()+index);
            root->left = constructMaximumBinaryTree(leftnums);
        }
        if(index < nums.size()-1)
        {
            vector<int> rightnums(nums.begin()+index+1,nums.end());
            root->right = constructMaximumBinaryTree(rightnums);
        }
        return root;
    }
};

为了写成框架，我们改写为如下代码：

// 主函数
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
    return build(nums, 0, nums.size() - 1);
}

// 定义：将 nums[lo..hi] 构造成符合条件的树，返回根节点
TreeNode* build(vector<int>& nums, int lo, int hi) {
    // base case
    if (lo > hi) {
        return nullptr;
    }

    // 找到数组中的最大值和对应的索引
    int index = -1, maxVal = INT_MIN;
    for (int i = lo; i <= hi; i++) {
        if (maxVal < nums[i]) {
            index = i;
            maxVal = nums[i];
        }
    }

    // 先构造出根节点
    TreeNode* root = new TreeNode(maxVal);
    // 递归调用构造左右子树
    root->left = build(nums, lo, index - 1);
    root->right = build(nums, index + 1, hi);
    
    return root;
}

4.2 通过前序和中序遍历构造二叉树

力扣第 105 题「从前序和中序遍历序列构造二叉树」
构造二叉树首要问题：确定根节点的值，把根节点做出来，然后递归构造左右子树即可。

所以，我们如何找到相同的根节点呢？
对前序遍历而言，根节点就是第一个数，那怎么将两个的左右子树对应起来呢？

class Solution {
public:

    // 存储 inorder 中值到索引的映射
    unordered_map<int, int> valToIndex;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
            for(int i= 0;i <= inorder.size() - 1 ;i++)
            {
                valToIndex[inorder[i]] = i;
            }
            return build(preorder,0,preorder.size()-1, inorder,0,inorder.size()-1);
    }

    TreeNode* build(vector<int>& preorder, int preStart, int preEnd, 
        vector<int>& inorder, int inStart, int inEnd)
        {
            if(preStart>preEnd)
            {
                return nullptr;
            }
            int rootpre = preorder[preStart];
            int index = valToIndex[rootpre];
            int leftsize = index - inStart;
            // int index = 0;
            // for(int i = inStart; i <= inEnd ; i++)
            // {
            //     if(inorder[i] == rootpre)
            //     {
            //         index = i;
            //         break;
            //     }
            // }
            TreeNode* root = new TreeNode(rootpre);

            root->left = build(preorder, preStart+1, preStart+leftsize,
                      inorder, inStart, index-1);

            root->right = build(preorder, preStart+leftsize+ 1, preEnd,
                       inorder, index+1, inEnd);
            return root;
        }
};

4.3 后序和中序遍历构造二叉树

力扣第 106 题「从后序和中序遍历序列构造二叉树」
该题和上文代码框架基本一致：

同样，我们根据中序遍历，找到 lefisize 找到左子树

class Solution {
public:
    unordered_map<int,int>mp;
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
            for(int i =0 ; i<inorder.size();i++)
            {
                mp[inorder[i]] = i;
            }
            return build(inorder,0,inorder.size()-1,
                         postorder,0,postorder.size()-1);
    }

    TreeNode* build(vector<int>& inorder, int instart,int inend,
                    vector<int>& postorder, int posstart, int posend)
        {
            if(posstart > posend)
            {
                return nullptr;
            }
            int rootval = postorder[posend];
            int index = mp[rootval];
            int leftsize = index - instart;

            TreeNode* root = new TreeNode(rootval);
            root->left = build(inorder,instart,index-1,
                                postorder,posstart,posstart+leftsize-1);
            root->right = build(inorder,index+1,inend,
                                postorder,posstart+leftsize,posend-1);
            return root;
        }
};

4.4 后序和前序遍历构造二叉树

力扣第 889 题「根据前序和后序遍历构造二叉树」
代码大致框架都和上文一样，只是再找这个 index 的时候需要好好查询。

lass Solution {
public:
    unordered_map<int,int>mp;
    TreeNode* constructFromPrePost(vector<int>& preorder, vector<int>& postorder) {
        for(int i= 0; i < postorder.size() ; i++)
        {
            mp[postorder[i]] = i;
        }
        return build(preorder,0,preorder.size()-1,
                    postorder,0,postorder.size()-1);
    }
    TreeNode* build(vector<int>& preorder,int prestart,int preend,
                    vector<int>& postorder, int posstart, int posend)
    {
        if(prestart > preend)
        {
            return nullptr;
        }
        if (prestart == preend) {
            return new TreeNode(preorder[prestart]);
        }
        int rootval = preorder[prestart];
        int index = mp[preorder[prestart + 1]];
        int leftsize = index - posstart + 1;

        TreeNode* root = new TreeNode(rootval);
        root->left = build(preorder,prestart+1,prestart+leftsize,
                            postorder,posstart,index);
        root->right = build(preorder,prestart+leftsize+1,preend,
                            postorder,index+1,posend-1);
        return root;
    }
};

为什么需要判断这个代码呢？

        if (prestart == preend) {
            return new TreeNode(preorder[prestart]);
        }

因为上文中这一步我们 prestart+1 ， 如果不判断，超出范围。

        int index = mp[preorder[prestart + 1]];

五：二叉树序列化问题

5.1 前中后序的二叉树唯一性

如果，前序遍历，比如不包含空指针，[1,2,3,4,5]，那么前序遍历会有很多情况，如下图：

如果前序遍历包含空指针，如下：左侧的二叉树的前序遍历结果就是 [1,2,3,#,#,4,#,#,5,#,#]，上图右侧的二叉树的前序遍历结果就是 [1,2,#,3,#,#,4,5,#,#,#]，它俩就区分开了。
所以，前中后都能唯一？不，只有前后遍历可以唯一，中序不行。
总结：
1 .序列不包含空指针，并且只给出一种遍历顺序，不能还原唯一
2 .如果不包含空指针，给出两种遍历顺序
###2.1 前中 或者 后中，均可以还原唯一
###2.2 如果只有前后，则也不能唯一还原
3 .如果包含空指针，只给出一种遍历顺序
###3.1 前后均可以
###3.2 中序不行

5.2 题解

力扣第 297 题「二叉树的序列化与反序列化」

5.3 前序遍历解法

前序太熟悉不过了，直接看模板：

list<int> res;
void traverse(TreeNode* root) {
    if (root == nullptr) {
        // 暂且用数字 -1 代表空指针 null
        res.push_back(-1);
        return;
    }

    /****** 前序位置 ******/
    res.push_back(root->val);
    /***********************/

    traverse(root->left);
    traverse(root->right);
}

如此前序遍历，直接看下图，我们直接将二叉树变成了一维数组。

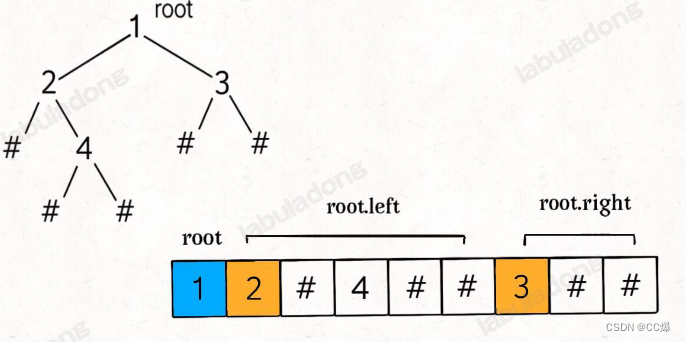
二叉树变成一个字符串，也是同理：

// 代表分隔符的字符
string SEP = ",";
// 代表 null 空指针的字符
string NULL = "#";
// 用于拼接字符串
stringstream ss;

/* 将二叉树打平为字符串 */
void traverse(TreeNode* root, stringstream& ss) {
    if (root == NULL) {
        ss << NULL << SEP;
        return;
    }

    /****** 前序位置 ******/
    // str += to_string(root-val) + ”，“ ； 
    ss << root->val << SEP;
    /***********************/

    traverse(root->left, ss);
    traverse(root->right, ss);
}

六：归并排序问题

这里涉及到二叉树问题，就简单初步了解阐述一下：
归并就是，先将左半边的数组排好序，再把右边排好序，最后合并起来。
归并排序的代码框架：

// 定义：排序 nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
    if (lo == hi) {
        return;
    }
    int mid = (lo + hi) / 2;
    // 利用定义，排序 nums[lo..mid]
    sort(nums, lo, mid);
    // 利用定义，排序 nums[mid+1..hi]
    sort(nums, mid + 1, hi);

    /****** 后序位置 ******/
    // 此时两部分子数组已经被排好序
    // 合并两个有序数组，使 nums[lo..hi] 有序
    merge(nums, lo, mid, hi);
    /*********************/
}

// 将有序数组 nums[lo..mid] 和有序数组 nums[mid+1..hi]
// 合并为有序数组 nums[lo..hi]
void merge(int[] nums, int lo, int mid, int hi);
//该函数属于合并函数，此处没有具体写完，了解为合并函数就行。

这么一看，对归并排序，就更加明显了，属于明显二叉树。

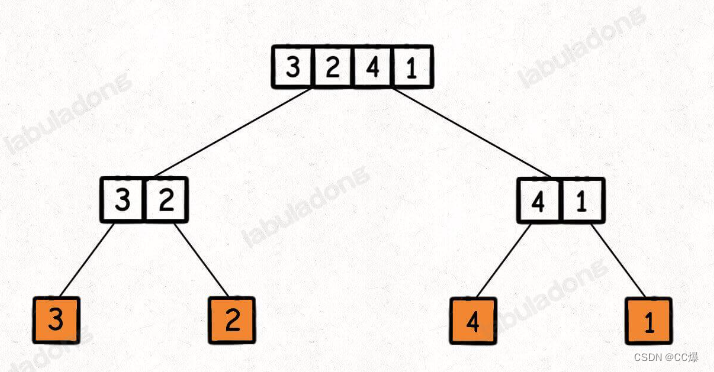
可以分为左右子树进行排序，排序结束就合并

七：二叉搜索树（特性）

7.1 二叉搜索树基础

二叉搜索树（BST）
1 . BST 的每一个节点 node ，左子树值都比 node 小，右子树值都比 node 大。
2 .对于 BST 的左右侧子树也都是 BST。
最重要的一点： BST 的中序遍历结果是有序的 ，还是升序
可以以中序遍历结果，将二叉树 升序结果打印出来。

void traverse(TreeNode* root) 
{
    if (root == nullptr) 
    {
       return;
    }
    traverse(root->left);
    // 中序遍历代码位置
    print(root->val);
    traverse(root->right);
}

7.2 寻找第K小的元素

力扣第 230 题「二叉搜索树中第 K 小的元素」
该方法存在问题：因为查找得遍历一次，会增加复杂度问题。

    int res = 0;
    int rank =0;
    int kthSmallest(TreeNode* root, int k) 
    {
        traverse(root,k);
        return res;
    }

    void traverse(TreeNode* root,int k)
    {
        if(root == nullptr)
        {
            return ;
        }
        traverse(root->left , k);

        rank++;
        if(k == rank)
        {
            res = root->val;
            return;
        }

        traverse(root->right,k);
    }

7.3 BST转化累加树

力扣第 538 题「把二叉搜索树转换为累加树」
因为需要累加，中序遍历又是升序，所以直接倒转一下：

void traverse(TreeNode* root) {
    if (root == nullptr) return;
    // 先递归遍历右子树
    traverse(root->right);
    // 中序遍历代码位置
    print(root->val);
    // 后递归遍历左子树
    traverse(root->left);
}

然后再进行累加，即可完成，完整代码如下：

class Solution {
public:
int sum = 0;
    TreeNode* convertBST(TreeNode* root) {
        traverse(root);
        return root;
    }
    void traverse(TreeNode* root)
    {
        if(root == nullptr)
        {
            return;
        }
        if(root->right) traverse(root->right);
        //此处累加和
        sum += root->val;
        root->val = sum;
        if(root->left) traverse(root->left);
    }
};

八：二叉搜索树（基本操作）

BST的基础主要是之前描述过的（左小右大）的特性，所以用于二分搜索效率很高。

void BST(TreeNode* root, int target) {
    if (root->val == target)
        // 找到目标，做点什么
    if (root->val < target) 
        BST(root->right, target);
    if (root->val > target)
        BST(root->left, target);
}

8.1 判断BST的合法性

力扣第 98 题「验证二叉搜索树」
最初的思路，直接进行判断，左右节点和根节点对比，判断 true 与 false

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        if(root == nullptr)
        {
            return true;
        }
        if(root->left)
        {
            if(root->left->val >= root->val)
            {
                return false;
            }
        }
        if(root->right)
        {
            if(root->right->val <= root->val )
            {
                return false;
            }
        }
        return isValidBST(root->left)&&isValidBST(root->right);
    }
};

但是这个代码有问题，不能全部通过，如下图：

原因：root 的整个左子树都要小于 root->val,整个右子树都要大于 root->val。

class Solution {
public:
    bool isValidBST(TreeNode* root) {
        return isValidBST(root,nullptr,nullptr);
    }
    bool isValidBST(TreeNode* root, TreeNode* min , TreeNode* max)
    {
        if(root == nullptr)
        {
            return true;
        }
        if(min != nullptr)
        {
            if(min->val >= root->val)
            {
                return false;
            }
        }
        if(max != nullptr)
        {
            if(max->val <= root->val)
            {
                return false;
            }
        }
        return isValidBST(root->left, min, root) && isValidBST(root->right, root, max);
    }
};

8.2在BST中搜索元素

力扣第 700 题「二叉搜索树中的搜索」
我自己的写法：
但是这个写法属于是二叉树写法，属于是都遍历了。

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr)
        {
            return root;
        }
        if(root->val == val)
        {
            return root;
        }
        TreeNode* left = searchBST(root->left,val);
        TreeNode* right = searchBST(root->right,val);
        // 这行代码的意义是，如果左边找到了，就直接返回左边，找不到在返回右子树
        return left != nullptr ? left : right;
    }
};

下面，我尝试写出二叉搜索树的写法：

class Solution {
public:
    TreeNode* searchBST(TreeNode* root, int val) {
        if(root == nullptr)
        {
            return root;
        }
        // 进行判断，如果根节点大于 val 则往左子树进行查询
        if(root->val > val )
        {
           return  searchBST(root->left,val);
        }
        //如果根节点小于 val 则往右子树进行查询
        if(root->val < val)
        {
            return searchBST(root->right,val);
        }
        return root;
    }
};

8.3 BST中插入一个数

插入一个数： 先遍历找到插入位置，在进行插入。

TreeNode* insertIntoBST(TreeNode* root, int val) {
    // 找到空位置插入新节点
    if (root == nullptr) return new TreeNode(val);
    // if (root->val == val)
    //     BST 中一般不会插入已存在元素
    if (root->val < val) 
        root->right = insertIntoBST(root->right, val);
    if (root->val > val) 
        root->left = insertIntoBST(root->left, val);
    return root;
}

8.4 BST删除一个数

同样道理，先找到，再删除。

TreeNode* deleteNode(TreeNode* root, int key) {
    if (root->val == key) {
        // 找到啦，进行删除
    } else if (root->val > key) {
        // 去左子树找
        root->left = deleteNode(root->left, key);
    } else if (root->val < key) {
        // 去右子树找
        root->right = deleteNode(root->right, key);
    }
    return root;
}

删除，如何删除呢？上文代码框架只能找到位置。
删除也有几种状况如下：
1 .A 恰好是末端节点，两个子节点都为空，那么它可以当场去世了

	//删除节点，如果为末节点，则直接返回 null
	if(root->left == nullptr && root->right == nullptr)
	{
		return null;
	}

2 .A 只有一个非空子节点，那么它要让这个孩子接替自己的位置。

	// 只有一个子节点的状况
	if(root->left == null) return root->right;
	if(root->right== null) return root->left;

3 .A 有两个子节点，麻烦了，为了不破坏 BST 的性质，A 必须找到左子树中最大的那个节点，或者右子树中最小的那个节点来接替自己。

if (root.left != null && root.right != null) {
    // 找到右子树的最小节点
    TreeNode minNode = getMin(root.right);
    // 把 root 改成 minNode
    root.val = minNode.val;
    // 转而去删除 minNode
    root.right = deleteNode(root.right, minNode.val);
}

此时，三种情况都分析结束，下问则是整体框架代码：

// 在 BST 中删除节点
TreeNode deleteNode(TreeNode root, int key) {
    // 当根节点为空，则直接返回 null
    if (root == null) return null;
    if (root.val == key) {
        // 当节点为叶子节点或者只有一个子节点时，直接返回该子节点
        if (root.left == null) return root.right;
        if (root.right == null) return root.left;
        // 当节点有两个子节点时，用其右子树最小的节点代替该节点
        TreeNode minNode = getMin(root.right);
        root.right = deleteNode(root.right, minNode.val);
        minNode.left = root.left;
        minNode.right = root.right;
        root = minNode;
    } else if (root.val > key) {
        // 删除节点在左子树中
        root.left = deleteNode(root.left, key);
    } else if (root.val < key) {
        // 删除节点在右子树中
        root.right = deleteNode(root.right, key);
    }
    return root;
}

// 获取以 node 为根节点的 BST 中最小的节点
TreeNode getMin(TreeNode node) {
    while (node.left != null) node = node.left;
    return node;
}

九：二叉搜索树（构造）

9.1不同的二叉树搜索树

力扣第 96 题「不同的二叉搜索树」
重点还是4个字：左小右大。比如 1到5，以3为根节点，那么，左子树就是 12，右子树就是 45.

具体多少个，就是你的 left * right。
由此，可以写出代码框架：

class Solution {
public:
    int numTrees(int n) {
        return count(1,n);
    }
    int count(int left,int right)
    {
        if(left > right)
        {
            return 1;
        }
        int res  = 0;
        for(int i = left ; i<=right ; i++)
        {
            int leftnum = count(left, i-1);
            int rightnum = count(i+1,right);
            res += leftnum*rightnum;
        }
        return res;
    }
};

这部分代码就是，假设 i 为根节点的时候，左右子树的种数：

        for(int i = left ; i<=right ; i++)
        {
            int leftnum = count(left, i-1);
            int rightnum = count(i+1,right);
            res += leftnum*rightnum;
        }

注意 base case，显然当 lo > hi 闭区间 [lo, hi] 肯定是个空区间，也就对应着空节点 null，虽然是空节点，但是也是一种情况，所以要返回 1 而不能返回 0。
但是这个模板存在问题，那就是时间复杂度非常的高，存在重叠子问题。
然后涉及动态规划消除重叠子问题，加个备忘录。

class Solution {
public:
vector<vector<int>>num;
    int numTrees(int n) {
        num = vector<vector<int>>(n + 1, vector<int>(n + 1, 0));
        return count(1,n);
    }
    int count(int left,int right)
    {
        if(left > right)
        {
            return 1;
        }
        if(num[left][right] != 0)
        {
            return num[left][right];
        }
        int res  = 0;
        for(int i = left ; i<=right ; i++)
        {
            int leftnum = count(left, i-1);
            int rightnum = count(i+1,right);
            res += leftnum*rightnum;
        }
        num[left][right] = res;
        return res;
    }
};

这道题可以直接使用动态规划：
这个动态规划目前有点迷糊，具体求解后续多思考。

    int numTrees(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;
        dp[1] = 1;

        for (int i = 2; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                dp[i] += dp[j - 1] * dp[i - j];
            }
        }

        return dp[n];
    }

9.2 不同搜索二叉树升级版

力扣第 95 题「不同的二叉搜索树 II」
思路和上文基本一致，对左右子树进行排列，然后进行排列。

class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        if(n == 0)
        {
            return vector<TreeNode*>{};
        }
        return count(1,n);
    }

    vector<TreeNode*> count(int left,int right)
    {
        vector<TreeNode* >res;
        if(left > right)
        {
            res.push_back(nullptr) ;
            return res;
        }

        for(int i = left; i<=right;i++)
        {
        	// 这是存储左右子树的所有情况。
            vector<TreeNode* > leftnode = count(left,i-1);
            vector<TreeNode* > rightnode = count(i+1,right);
            
            // 左右子树情况遍历，同上文的 left*right种类数
            for(auto left : leftnode)
            {
                for(auto right : rightnode)
                {
                    TreeNode* root = new TreeNode(i);
                    root->left = left;
                    root->right = right;
                    res.push_back(root);
                }
            }
        }
        return res;
    }
};

十：快速排序详解

首先先看看快排的框架：

void sort(int nums[], int lo, int hi) {
    if (lo >= hi) {
        return;
    }
    // 对 nums[lo..hi] 进行切分
    // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
    int p = partition(nums, lo, hi);
    // 去左右子数组进行切分
    sort(nums, lo, p - 1);
    sort(nums, p + 1, hi);
}

这个快排，和二叉树基本也是一致的，但是其中 partition 函数很重要。 partition 函数的作用是在 nums[lo…hi] 中寻找一个切分点 p，通过交换元素使得 nums[lo…p-1] 都小于等于 nums[p]，且 nums[p+1…hi] 都大于 nums[p]：

从二叉树视角进行：这个排序得到的还是搜索二叉树。

代码框架：

class QuickSort {
public:
    static void sort(std::vector<int>& nums) {
        // 为了避免出现耗时的极端情况，先随机打乱
        shuffle(nums);
        // 排序整个数组（原地修改）
        sort(nums, 0, nums.size() - 1);
    }

private:
    static void sort(std::vector<int>& nums, int lo, int hi) {
        if (lo >= hi) {
            return;
        }
        // 对 nums[lo..hi] 进行切分
        // 使得 nums[lo..p-1] <= nums[p] < nums[p+1..hi]
        int p = partition(nums, lo, hi);

        sort(nums, lo, p - 1);
        sort(nums, p + 1, hi);
    }

    // 对 nums[lo..hi] 进行切分
    static int partition(std::vector<int>& nums, int lo, int hi) {
        int pivot = nums[lo];
        // 关于区间的边界控制需格外小心，稍有不慎就会出错
        // 我这里把 i, j 定义为开区间，同时定义：
        // [lo, i) <= pivot；(j, hi] > pivot
        // 之后都要正确维护这个边界区间的定义
        int i = lo + 1, j = hi;
        // 当 i > j 时结束循环，以保证区间 [lo, hi] 都被覆盖
        while (i <= j) {
            while (i < hi && nums[i] <= pivot) {
                i++;
                // 此 while 结束时恰好 nums[i] > pivot
            }
            while (j > lo && nums[j] > pivot) {
                j--;
                // 此 while 结束时恰好 nums[j] <= pivot
            }

            if (i >= j) {
                break;
            }
            // 此时 [lo, i) <= pivot && (j, hi] > pivot
            // 交换 nums[j] 和 nums[i]
            swap(nums[i], nums[j]);
            // 此时 [lo, i] <= pivot && [j, hi] > pivot
        }
        // 最后将 pivot 放到合适的位置，即 pivot 左边元素较小，右边元素较大
        swap(nums[lo], nums[j]);
        return j;
    }

    // 洗牌算法，将输入的数组随机打乱
    static void shuffle(std::vector<int>& nums) {
        std::random_device rd;
        std::mt19937 gen(rd());
        int n = nums.size();
        for (int i = 0; i < n; i++) {
            // 生成 [i, n - 1] 的随机数
            std::uniform_int_distribution<int> dis(i, n - 1);
            int r = dis(gen);
            swap(nums[i], nums[r]);
        }
    }

    // 原地交换数组中的两个元素
    static void swap(int& a, int& b) {
        int temp = a;
        a = b;
        b = temp;
    }
};

十一：LCA（最近公共祖先）

这道题，属于是查询到公共祖先，和上文我们了解到的，查询树中的值为 val 的节点，相同模板：
这是前序遍历查询是否存在相同值的节点：

TreeNode* find(TreeNode* root, int val) {
    if (root == nullptr) {
        return nullptr;
    }
    // 前序位置
    if (root->val == val) {
        return root;
    }
    // root 不是目标节点，去左右子树寻找
    TreeNode* left = find(root->left, val);
    TreeNode* right = find(root->right, val);
    // 看看哪边找到了
    return left != nullptr ? left : right;
}

力扣第 236 题「二叉树的最近公共祖先」：

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        return find(root,p->val,q->val);
    }
    TreeNode* find(TreeNode* root , int val1 , int val2)
    {
        if(root == NULL)
        {
            return NULL;
        }
        if(root->val == val1 || root->val == val2)
        {
            return root;
        }
        TreeNode* left = find(root->left,val1,val2);
        TreeNode* right = find(root->right,val1,val2);

        if(left != NULL && right != NULL)
        {
            return root;
        }
        return left != NULL ? left : right;
    }
};

十二：如何计算完全二叉树节点

12.1 思路

我们首先想想如何求一颗完全二叉树节点呢？
我们先看看普通二叉树：

int countNodes(TreeNode* root) {
    if (root == nullptr) return 0;
    return 1 + countNodes(root->left) + countNodes(root->right);
}

那满二叉树呢？节点就是 层数的2次方 - 1：

int countNodes(TreeNode* root) {
    int h = 0;
    // 计算树的高度 因为是满二叉树，所以 左右子树都无所谓
    while (root != nullptr) {
        root = root->left;
        h++;
    }
    // 节点总数就是 2^h - 1
    return pow(2, h) - 1;
}

但是完全二叉树就存问题了，因为他没有满二叉树，计算他的节点总数，结合上面两个模板：

int countNodes(TreeNode* root) {
    TreeNode* l = root, * r = root;
    // 沿最左侧和最右侧分别计算高度
    int hl = 0, hr = 0;
    while (l != nullptr) {
        l = l->left;
        hl++;
    }
    while (r != nullptr) {
        r = r->right;
        hr++;
    }
    // 如果左右侧计算的高度相同，则是一棵满二叉树
    if (hl == hr) {
        return pow(2, hl) - 1;
    }
    // 如果左右侧的高度不同，则按照普通二叉树的逻辑计算
    return 1 + countNodes(root->left) + countNodes(root->right);
}

如下图，一看便知：