本文介绍了数组操作中的双指针技巧，如删除有序数组的重复项、移除元素以及移动0。此外，还探讨了前缀和在数组和矩阵中的应用，以及如何构建乘积数组。同时，讲解了滑动窗口在寻找子数组和字符异位词中的应用，并展示了如何高效地找到数组中和为K的子数组。最后，提到了几种数组遍历和旋转图像的方法。
目录
双指针用法
26删除有序数组的重复项
- 这道题就很能体现数组的特性，我们找到数组是连续存储的，如果你想删除数组的一个元素，那么你必须去让这个元素之后的所有元素去往前覆盖一个元素，所以这道题，让我们去返回剩余元素的长度，其实并不是真的像链表那种将元素之间的连接断开
- 这题的思路就是双指针，我们用一个指针指向第一个元素，另一个也指向第一个元素，第一个元素是用来指向无序元素的最后一个索引，另一个指针来判断是否是重复的元素
class Solution { public int removeDuplicates(int[] nums) { int n1=0; int n2=0; while (n2<nums.length){ if (nums[n1]==nums[n2]){ n2++; }else { n1++; nums[n1]=nums[n2]; n2++; } } return n1+1; } }对比链表的数据结构
- 链表我们需要通过next这种连接来遍历链表，其删除节点也非常简单，只需要断开相应的连接即可，这就是基于不同的数据结构，有不同的解决方法
ListNode deleteDuplicates(ListNode head) { if (head == null) return null; ListNode slow = head, fast = head; while (fast != null) { if (fast.val != slow.val) { // nums[slow] = nums[fast]; slow.next = fast; // slow++; slow = slow.next; } // fast++ fast = fast.next; } // 断开与后面重复元素的连接 slow.next = null; return head; }
27移除元素
class Solution { public int removeDuplicates(int[] nums) { int n1=0; int n2=0; while (n2<nums.length){ if (nums[n1]==nums[n2]){ n2++; }else { n1++; nums[n1]=nums[n2]; n2++; } } return n1+1; } }
283移动0
class Solution { public void moveZeroes(int[] nums) { //其实就是变形了一下，将0的元素全删除,留下前面的都是不为0的元素，把数组剩余的空间值都赋值为0 int p= remove(nums,0); for (int i = p; i <nums.length ; i++) { nums[i]=0; } } private int remove(int[] nums, int i) { int slow=0; int fast=0; while (fast<nums.length){ if (nums[fast]!=0){ nums[slow]=nums[fast]; fast++; slow++; }else { fast++; } } return slow; } }
左右指针
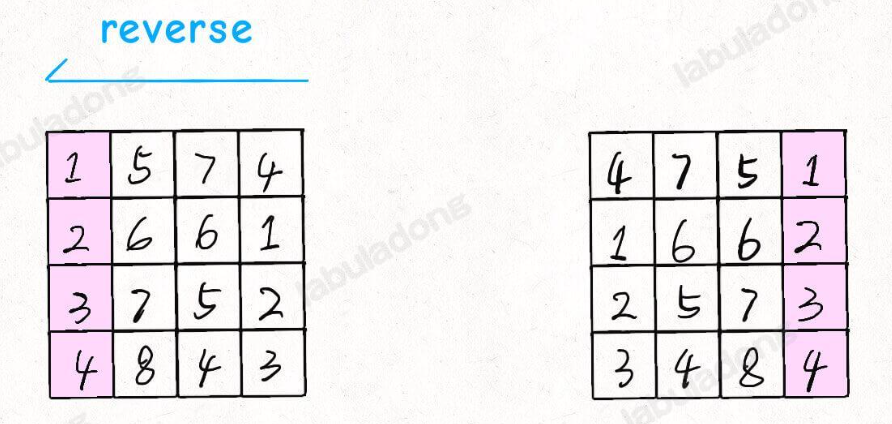
334反转字符串
class Solution { public void reverseString(char[] s) { int left=0; int right=s.length-1; while (left<right){ char temp=s[left]; s[left]=s[right]; s[right]=temp; left++; right--; } } }
Offer 57和为S的两个数字
class Solution { public int[] twoSum(int[] nums, int target) { int left=0; int right=nums.length-1; while (left<right){ if (nums[left]+nums[right]==target){ int []arr={nums[left],nums[right]}; return arr; }else if (nums[left]+nums[right]>target){ right--; }else { left++; } } return null; } }
- 判断一个回文串，我们是通过从中间分开，看后面那一部分的逆序和前面一部分是否相同
- 但是找一个回文串，我们应该从中间结点，然后向两端去判断加两个字符是否还是回文串，但是难点是我们知道回文串可能是偶数也可能是奇数个节点，我们可以通过一次传入两个节点，作为其中间节点，如果是奇数个节点，那么我们把中间节点传入两遍
- 我们遍历字符串，将每一个节点，或者每两个节点作为中心节点，然后找出最长的回文字符串
class Solution { public String longestPalindrome(String s) { String res=""; for (int i = 0; i < s.length(); i++) { String str1=findPalindrome(s,i,i);//找奇数个的节点回文串 String str2=findPalindrome(s,i,i+1);//找偶数个节点的回文串 res=str1.length()>res.length()?str1:res; res=str2.length()>res.length()?str2:res; } return res; } private String findPalindrome(String s, int left, int right) { while (left>=0&&right<s.length()&&s.charAt(left)==s.charAt(right)){ left--; right++; } return s.substring(left+1,right);//substring是左闭右开的 } }
数组技巧之前缀和
一维数组前缀和
前缀和技巧适用于快速、频繁地计算一个索引区间内的元素之和。
如何建立前缀和数组
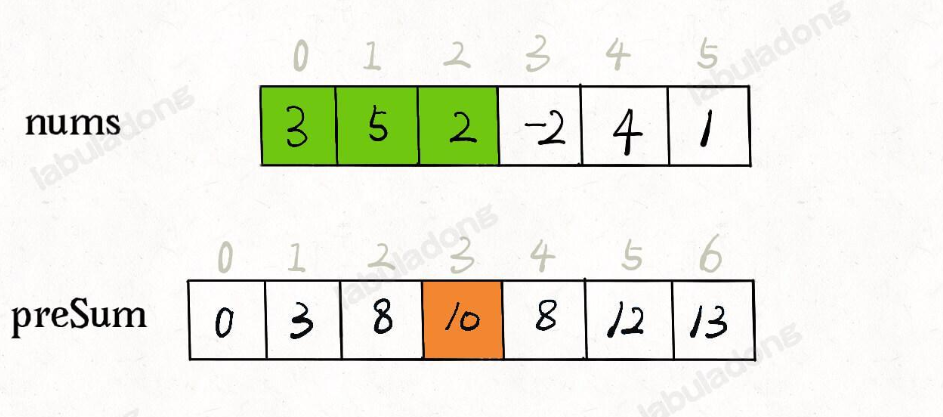
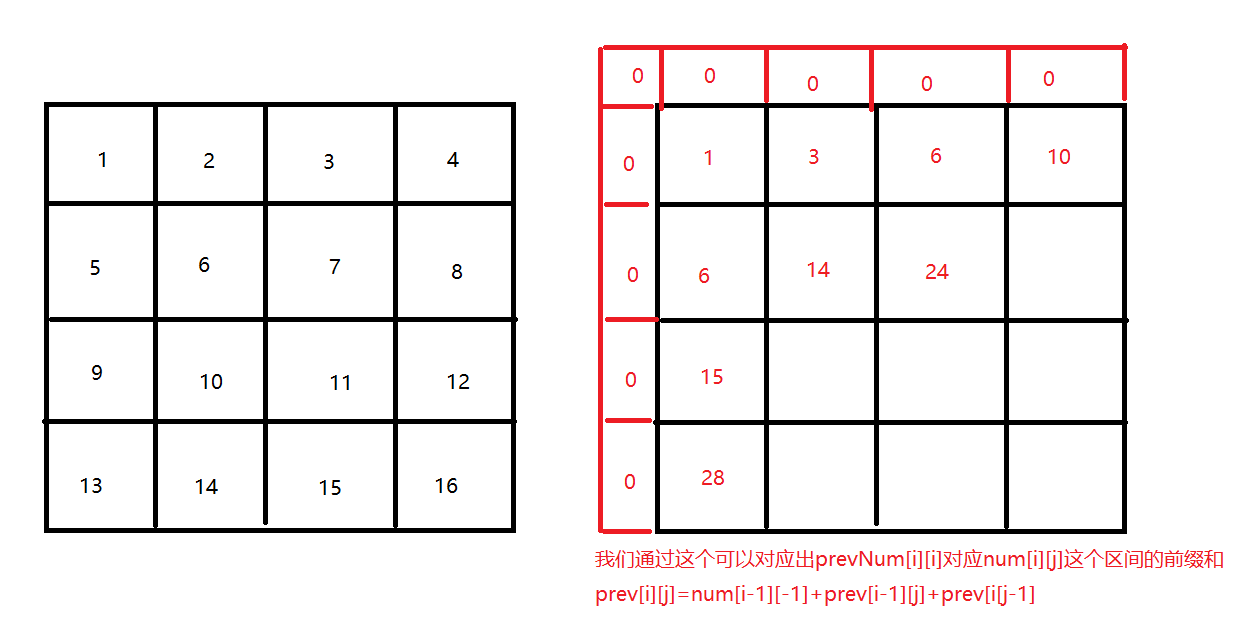
- 前缀和数组的构造，其新数组的大小比nums大1，其preSum[0]==nums[0],preSum[i]=preSum[i-1]+nums[i-1]
- preSum[i]表示nums[0]到nums[i-1]的之和
/* 输入一个数组，构造前缀和 */ public NumArray(int[] nums) { // preSum[0] = 0，便于计算累加和 preSum = new int[nums.length + 1]; // 计算 nums 的累加和 for (int i = 1; i < preSum.length; i++) { preSum[i] = preSum[i - 1] + nums[i - 1]; } }前缀和的作用
- 看这个
preSum数组，如果我想求索引区间[1, 4]内的所有元素之和，就可以通过preSum[5] - preSum[1]得出。class NumArray { int preNum[]; public NumArray(int[] nums) { //根据nums来构造前缀和数组 preNum=new int[nums.length+1]; preNum[0]=0;//因为preNum[i]表示num[i-1]到num[0]的之和 for (int i = 1; i <=nums.length; i++) { preNum[i]=preNum[i-1]+nums[i-1]; } } public int sumRange(int left, int right) { return preNum[right+1]-preNum[left]; } } /** * Your NumArray object will be instantiated and called as such: * NumArray obj = new NumArray(nums); * int param_1 = obj.sumRange(left,right); */二维矩阵中的前缀和
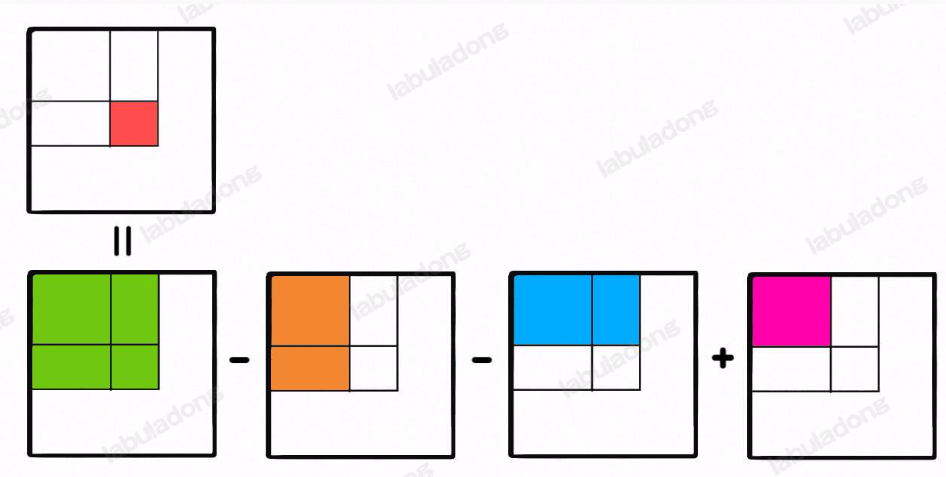
- 我们知道perNum[i][j]表示以num[i][j]为右下角，num[0][0] 为左下角，这个区间的所有元素之和
构造前驱二维数组
int row=matrix.length; int column=matrix[0].length; preNum=new int[row+1][column+1];//表示matrix[i-1][j-1]的到[0][0]的总的元素之和 for (int i = 1; i <=row ; i++) { for (int j = 1; j <=column; j++) { preNum[i][j]=preNum[i-1][j]+preNum[i][j-1]+matrix[i-1][j-1]-preNum[i-1][j-1]; } }
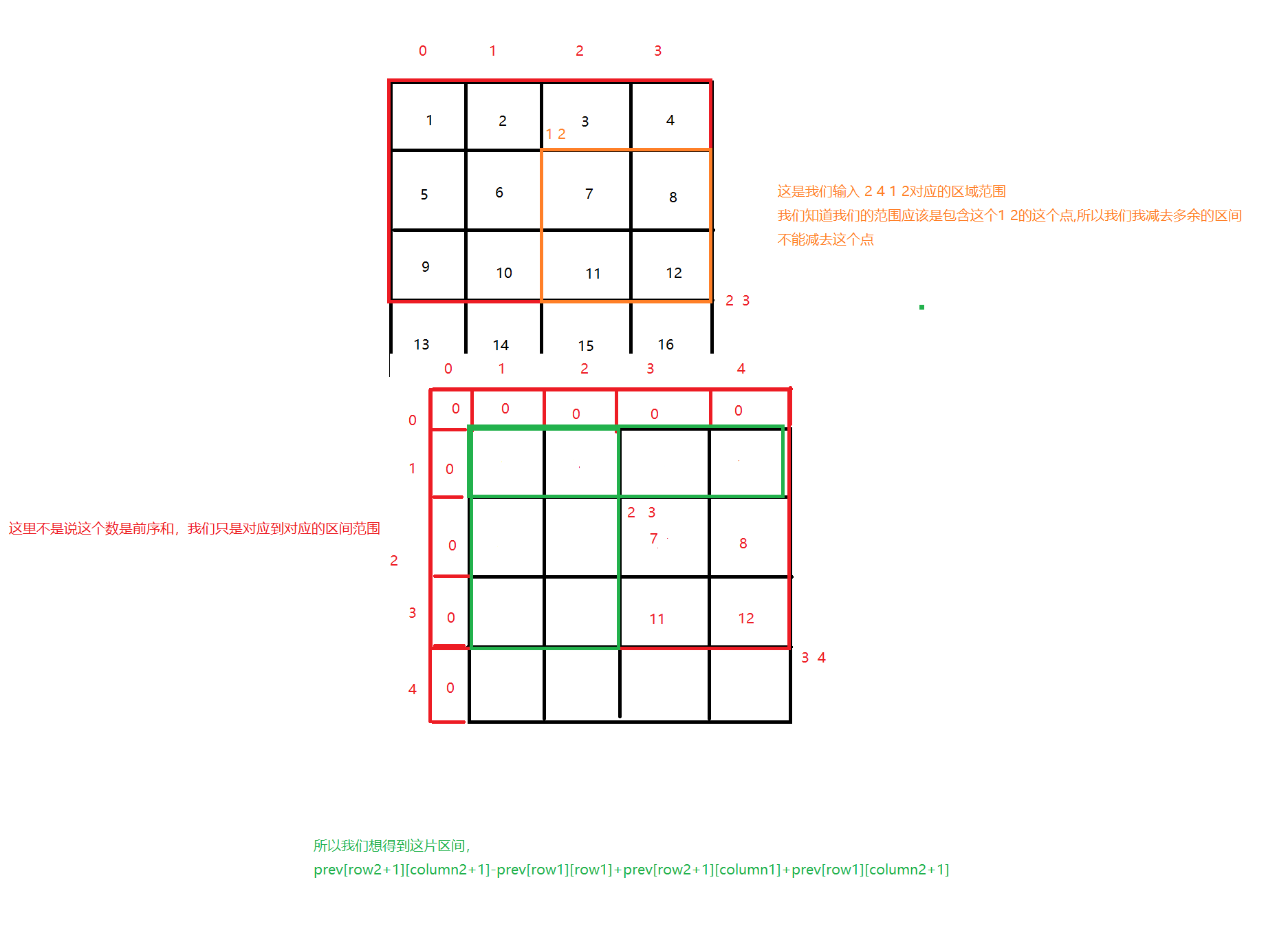
- 对于preNum[i][j],我们知道perNum[i][j]表示以num[i][j]为右下角，num[0][0] 为左下角，这个区间的所有元素之和,所以对于一个preNum[i][j]新添加的元素是matrix[i-1][j-1].那么对于构造
class NumMatrix { int preNum[][]; public NumMatrix(int[][] matrix) { if (matrix==null){ return; } int row=matrix.length; int column=matrix[0].length; preNum=new int[row+1][column+1];//表示matrix[i-1][j-1]的到[0][0]的总的元素之和 for (int i = 1; i <=row ; i++) { for (int j = 1; j <=column; j++) { preNum[i][j]=preNum[i-1][j]+preNum[i][j-1]+matrix[i-1][j-1]-preNum[i-1][j-1]; } } } public int sumRegion(int row1, int col1, int row2, int col2) { return preNum[row2+1][col2+1]-preNum[row1][col2+1]-preNum[row2+1][col1] +preNum[row1][col1]; } } /** * Your NumMatrix object will be instantiated and called as such: * NumMatrix obj = new NumMatrix(matrix); * int param_1 = obj.sumRegion(row1,col1,row2,col2); */
offer66构建乘积
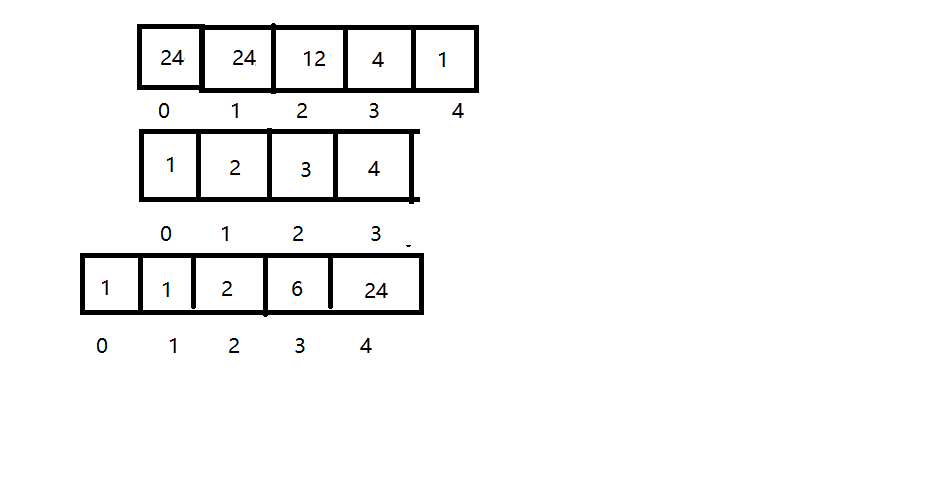
- 这道题的难点就是在于怎么去不用除法，我们的主要思路就是通过得到一个数的前面数据的乘积，和后面数据的乘积，这样我们就能得到其没有这个数据的乘积
- 这两个数据的求法就是前缀和的类似求法，只是要注意其下标
class Solution { public int[] constructArr(int[] a) { if (a==null||a.length==0){ return a; } //这道题要用两次前缀乘积得到数据 int prev[] = new int[a.length + 1]; int last[] = new int[a.length + 1]; prev[0] = 1; last[a.length] = 1; for (int i = 1; i <= a.length; i++) { prev[i] = prev[i - 1] * a[i-1]; } for (int i = a.length - 1; i >= 0; i--) { last[i] = last[i + 1] * a[i]; } int B[] = new int[a.length]; B[a.length-1]=prev[a.length-1]; for (int i = 0; i <a.length-1; i++) { B[i] = prev[i] * last[i + 1]; } return B; } }560. 和为 K 的子数组
package algorithm.Arrays.PrefixSum; public class Test560 { public int subarraySum(int[] nums, int k) { int count=0; int prev[]=new int[nums.length+1]; prev[0]=0; //构造前缀和数组 for (int i = 1; i <=nums.length; i++) { prev[i]=prev[i-1]+nums[i-1]; } for (int left = 0; left <nums.length; left++) { for (int right = left; right < nums.length; right++) { //[left,right] //通过前缀和来计算[right,left]的区间之和 if (prev[right+1]-prev[left]==k){ count++; } } } return count; } }
- 这种就是最普通的方法，但是这种方法会超时
- 我们这里只是需要找数为k的区间，我们用map记录每个前缀和的，如果每遇到一个前缀和为i的值，我们就去map中找是否有前缀和为i-k的存在，如果有，就将前缀和的为i-k的数据加到统计次数中
class Solution { public int subarraySum(int[] nums, int k) { int count=0; int prev[]=new int[nums.length+1]; prev[0]=0; //构造前缀和数组 for (int i = 1; i <=nums.length; i++) { prev[i]=prev[i-1]+nums[i-1]; } Map<Integer,Integer> map=new HashMap<>(); for (int i = 0; i < prev.length; i++) { // 如果有与当前prefixSum[i]的差为k的，则加上它的个数 //因为两个前缀和相差为k,说明是这个区间的值为k count+=map.getOrDefault(prev[i]-k,0); //统计前缀和的个数 map.put(prev[i],map.getOrDefault(prev[i],0 )+1); } return count; } }
二维数组的花式遍历
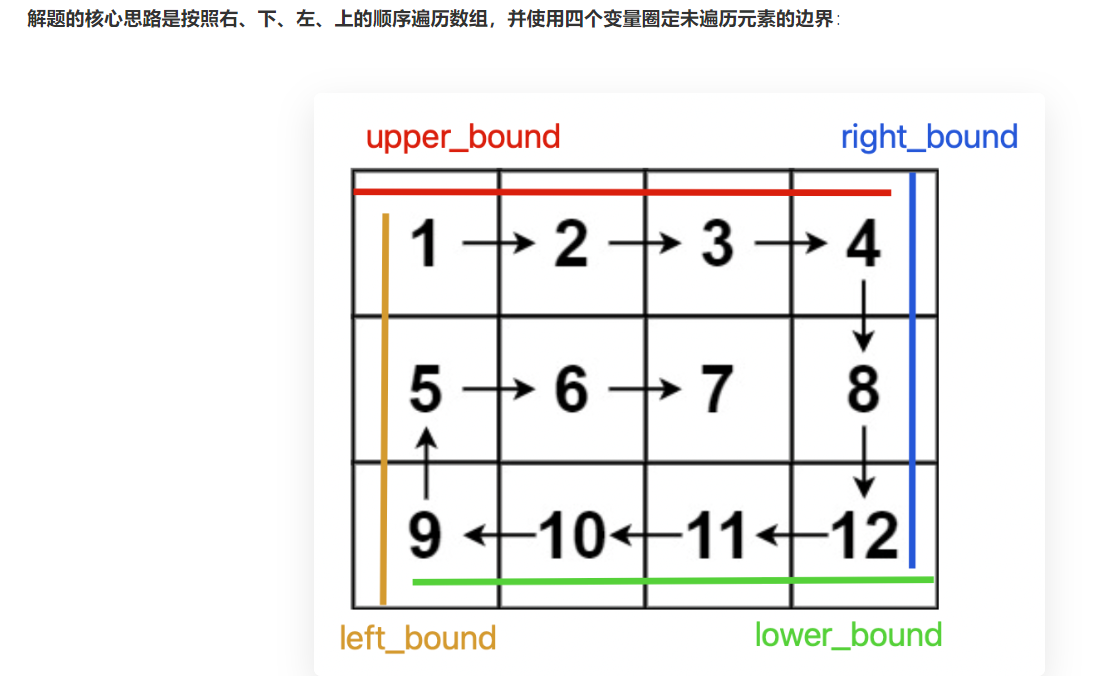
class Solution { public int[] spiralOrder(int[][] matrix) { int res[] = new int[0]; if (matrix==null||matrix.length==0){ return res; } int row=matrix.length; int column=matrix[0].length; int upper_bound=0;//上界 int lower_bound=row-1;//下界 int left_bound=0;//左界 int right_bound=column-1; int count=0; res=new int[row*column]; while (count<row*column){ //先从最上侧从左走向右 怎么保证还有路可以走 就是上边界(大于等于)下边界 if (upper_bound<=lower_bound){ for (int i = left_bound; i <=right_bound ; i++) { res[count]=matrix[upper_bound][i]; count++; } upper_bound++; //从最左侧走到最右侧 说明我们走完了一行,就需要将上边界++ } //先从最右侧从上往下走 怎么保证还有路可以走 就是左边界(小于等于)右边界 if (left_bound<=right_bound){ for (int i = upper_bound; i <=lower_bound ; i++) { res[count]=matrix[i][right_bound]; count++; } right_bound--; //从最右侧从上走到下 说明我们走完了一列,就需要将右边界-- } //从最下侧 从左走到右,如何保证有地方可以走 if (upper_bound<=lower_bound){ for (int i = right_bound; i >=left_bound ; i--) { res[count]=matrix[lower_bound][i]; count++; } lower_bound--; //从最左侧走到最右侧 说明我们走完了一行,就需要将上边界++ } //先从最左侧从下往上走 怎么保证还有路可以走 就是左边界(小于等于)右边界 if (left_bound<=right_bound){ for (int i = lower_bound; i >=upper_bound ; i--) { res[count]=matrix[i][left_bound]; count++; } //从最右侧从下走到上 说明我们走完了一列,就需要将右边界-- left_bound++; } } return res; } }48旋转图像
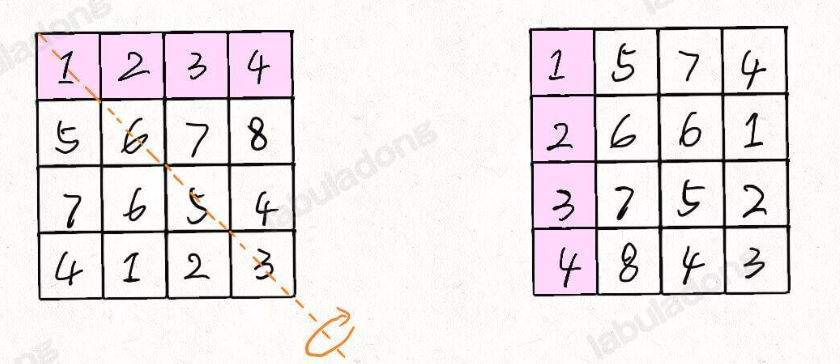
- 先将数组按照斜对角线交换，然后将每一行进行逆序
class Solution { public void rotate(int[][] matrix) { int n=matrix.length; for (int i = 0; i < n; i++) { for (int j = i; j <n; j++) { int temp=matrix[i][j]; matrix[i][j]=matrix[j][i]; matrix[j][i]=temp; } } for (int []arr:matrix) { int left=0; int right=n-1; while (left<right){ int temp=arr[left]; arr[left]=arr[right]; arr[right]=temp; left++; right--; } } } }
滑动窗口的应用
滑动窗口的核心框架
/* 滑动窗口算法框架 */ void slidingWindow(string s) { HashMap<char, int> window; int left = 0, right = 0; while (right < s.size()) { // c 是将移入窗口的字符 char c = s.charAt(i); // 增大窗口 right++; // 进行窗口内数据的一系列更新 ... /*** debug 输出的位置 ***/ printf("window: [%d, %d)\n", left, right); /********************/ // 判断左侧窗口是否要收缩 while (window needs shrink) { // d 是将移出窗口的字符 char d = s.charAt(i); // 缩小窗口 left++; // 进行窗口内数据的一系列更新 ... } } }
- 滑动窗口的最大应用就是子串问题
我们在字符串
S中使用双指针中的左右指针技巧，初始化left = right = 0，把索引左闭右开区间[left, right)称为一个「窗口」。PS：理论上你可以设计两端都开或者两端都闭的区间，但设计为左闭右开区间是最方便处理的。因为这样初始化
left = right = 0时区间[0, 0)中没有元素，但只要让right向右移动（扩大）一位，区间[0, 1)就包含一个元素0了。如果你设置为两端都开的区间，那么让right向右移动一位后开区间(0, 1)仍然没有元素；如果你设置为两端都闭的区间，那么初始区间[0, 0]就包含了一个元素。两种情况都会给边界处理带来不必要的麻烦。2、我们先不断地增加
right指针扩大窗口[left, right)，直到窗口中的字符串符合要求（包含了T中的所有字符）。3、此时，我们停止增加
right，转而不断增加left指针缩小窗口[left, right)，直到窗口中的字符串不再符合要求（不包含T中的所有字符了）。同时，每次增加left，我们都要更新一轮结果。4、重复第 2 和第 3 步，直到
right到达字符串S的尽头。76最小覆盖字串
package algorithm.Arrays.slideWindow; import java.util.HashMap; public class Test76 { public String minWindow(String s, String t) { HashMap<Character,Integer> window=new HashMap<>();//滑动窗口 HashMap<Character,Integer> need=new HashMap<>(); //need 用来存储我们需要的字符和对应的需要的字符的个数 for (int i = 0; i < t.length(); i++) { char c=t.charAt(i); need.put(c,need.getOrDefault(c,0)+1); } int left=0; int right=0; //区间的左闭右开的 int valid=0;//满足条件的字符个数 int start=0,len=Integer.MAX_VALUE;//用来确定符合条件的字符串 while (right<s.length()){ //c是即将要移入的字符 char c=s.charAt(right); //右移 扩大窗口 right++; //这一部分是模板，用于我们移动右指针,增大窗口 //------------------------------------- if (need.containsKey(c)){ window.put(c,window.getOrDefault(c,0)+1); if (window.get(c).equals(need.get(c))){ valid++; } } //这一部分是因题目不同,对窗口内的数据进行更新(新填一个字符，可能要更新对应map（window）数据) //------------------------------------- while (valid==need.size()){ //说明了当前我们的窗口的字符串已经满足了条件 //以下用来更新左边的范围 if (right-left<len){ start=left; len=right-left; //说明存在更短的窗口大小 } //------------------ //d是要移出去的字符 char d=s.charAt(left); //将left这个字符从窗口移除 left++; //满足条件,我们必须开始减少窗口的大小,这也滑动窗口的模板 //------------------- if (need.containsKey(d)){ //如果删除的这个字符是need里面的字符 if (window.get(d).equals(need.get(d))){ //如果现在窗口中这个字符的数量跟我们需要的字符数量一样,那么减去这个，这个字符就不满足要求了 valid--; } window.put(d,window.getOrDefault(d,0)-1); } //减少一个数据，有可能会让我们对应的map(need)数据会变化，不同的题目会有不同的情况 } } return len==Integer.MAX_VALUE?"":s.substring(start,start+len); } }
- 首先套核心的滑动窗口套路，左闭右开的窗口区间,left从0开始，right从0开始
- 当不满足条件的时候，首先一直让窗口变大（right++），直到满足了条件，当满足了条件，我们就一直减少窗口的大小（left--），直到不满足了条件，我们就继续让窗口变大，一直重复，直到right走到了数组的尽头
- 不同的就是关于，如何去判断是否满足了条件，和记录我们要保留的数据，这道题的判断，是靠两个map,window来记录窗口中字符和其对应的个数，need来记录我们需要的字符和其对应的个数，用vaild来记录我们满足的字符的个数，如果vaild==need.length，说明满足条件，小于就不满足
- 这里面有一个Java语法的注意点，就是Interger这是一个包装类，切回缓存频繁使用的数值，数值范围是-128到127，在次范围内会直接返回缓存值，如果超过了这个范围，会新new一个对象，不能用等于号，用equlas;
Integer a1 = 1234; Integer a2 = 1234; System.out.println(a1 == a2);//false System.out.println(a1.equals(a2));//true Integer a3 = 123; Integer a4 = 123; System.out.println(a3 == a4);//true System.out.println(a3.equals(a4));//true438找到字符串所有的字母异位词
class Solution { public List<Integer> findAnagrams(String s, String p) { List<Integer> res=new LinkedList<>();//用于存储我们的结果 HashMap<Character,Integer> window=new HashMap<>();//窗口的存储的信息 HashMap<Character,Integer> need=new HashMap<>(); //存储需要的对应的信息 for (int i = 0; i < p.length(); i++) { char c=p.charAt(i); need.put(c,need.getOrDefault(c,0)+1); } int left=0; int right=0; //定义左右指针 int valid=0;//我们这里维护的应该是一个定长的区间，如果 while (right<s.length()){ char c=s.charAt(right);//当前我们要进行插入的字符 right++; if (need.containsKey(c)){ //这个字符是我们需要的 window.put(c,window.getOrDefault(c,0)+1); if (need.get(c).equals(window.get(c))){ valid++; } } while (right-left==p.length()){ //当前窗口的大小等于了我们要找的字符串 if (valid==need.size()){ //因为我们这里要的是一个定长的结果 只能是abc bac这种 //所以满足条件不一定可以,比如abcd就不行 //所以在这个外面加了一个判断是当前窗口大小==需要字符串的长度 res.add(left); } char d=s.charAt(left);//我们要减去的窗口的字符 left++; //进行缩减窗口 if (need.containsKey(d)){ //减去的这个元素是我们需要的 if (window.get(d).equals(need.get(d))){ //当前元素的个数刚好是我们需要的，减去一个就不够了 valid--; } window.put(d,window.get(d)-1); } } } return res; } }
- 由于这道题中
[left, right)其实维护的是一个定长的窗口，窗口大小为t.size()。因为定长窗口每次向前滑动时只会移出一个字符，所以可以把内层的 while 改成 if，效果是一样的
public int lengthOfLongestSubstring(String s) { HashMap<Character,Integer> window=new HashMap<>(); int left=0; int right=0; int max=0; while (right<s.length()){ char c=s.charAt(right);//我们要更新的字符 right++; //窗口变大 //-------------------------------------------- window.put(c,window.getOrDefault(c,0)+1);//将这个数据放进去 数据处理 //-------------------------------------------- while (window.get(c)>1){ //说明当前字符串不满足了要求了 //窗口要减小 char d=s.charAt(left); left++; //----------------------- window.put(d,window.get(d)-1);//数据处理 } //---------------------------------------------- max=Math.max(right-left,max); } return max; }239滑动窗口的最大值
- 这道题，我们首先想到用优先级队列（堆）来解决问题，因为堆这种结构最大的功能就是k个元素中找到最大值，但是有一个致命的缺陷，我们窗口移动的时候，如果最左边的元素的这些里面最大的值（比如元素的 5 2 1 4）从5 2 1 到2 1 4，其中最大值应该是4，但是我们最移动的时候（堆中的元素从 5 2 1 变成 5 2 1 4），但是5并不是我们范围内的元素，但是堆没有这种功能，来判断是不是范围内元素，所以我们传入堆中的数据，传一个键值对，值和对应的索引
class Solution { public int[] maxSlidingWindow(int[] nums, int k) { PriorityQueue<int[]> window=new PriorityQueue<>(new Comparator<int[]>() { @Override public int compare(int[] o1, int[] o2) { return o1[0]!=o2[0]?o2[0]-o1[0]:o2[1]-o1[1]; } }); //将堆中先放入k个元素 for (int i = 0; i < k; i++) { window.offer(new int[]{nums[i],i}); } int []res=new int[nums.length-k+1]; res[0]=window.peek()[0];//取出当前堆中的最大元素 for (int i = k; i <nums.length; i++) { window.offer(new int[]{nums[i],i}); while (window.peek()[1]<i-k+1){ window.poll(); //移除最大元素,但是不属于当前窗口的 } res[i-k+1]= window.peek()[0]; } return res; } }利用单调队列来实现
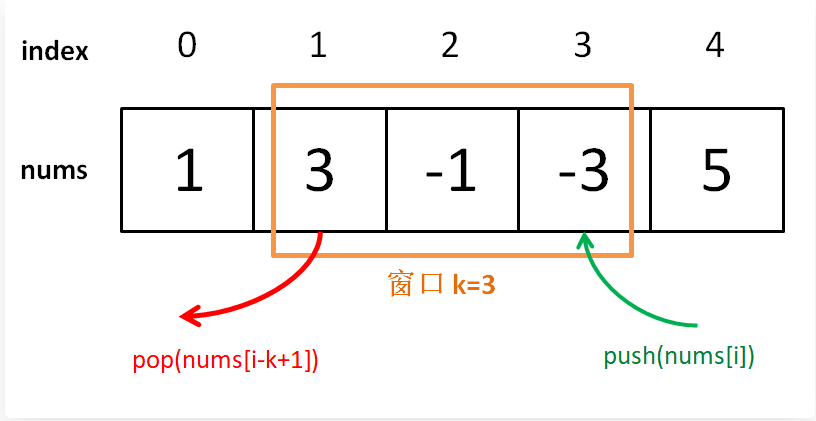
class Solution { class MonotonicQueue { LinkedList<Integer> dq = new LinkedList<>(); public void push(int n) { while (!dq.isEmpty() && n > dq.getLast()) { dq.pollLast(); } dq.addLast(n); //通过删除一起比要添加数字要小的元素,形成一个递减的队列 } public int max() { return dq.getFirst(); //第一个元素是最大值 } public void pop(int n) { if (n == dq.getFirst()) { dq.pollFirst(); } } } public int[] maxSlidingWindow(int[] nums, int k) { MonotonicQueue window=new MonotonicQueue(); List<Integer> res = new ArrayList<>(); for (int i = 0; i < nums.length; i++) { if (i<k-1){ window.push(nums[i]); }else { //窗口向前滑动一个大小 window.push(nums[i]); res.add(window.max()); window.pop(nums[i-k+1]); } } // 需要转成 int[] 数组再返回 int[] arr = new int[res.size()]; for (int i = 0; i < res.size(); i++) { arr[i] = res.get(i); } return arr; } }
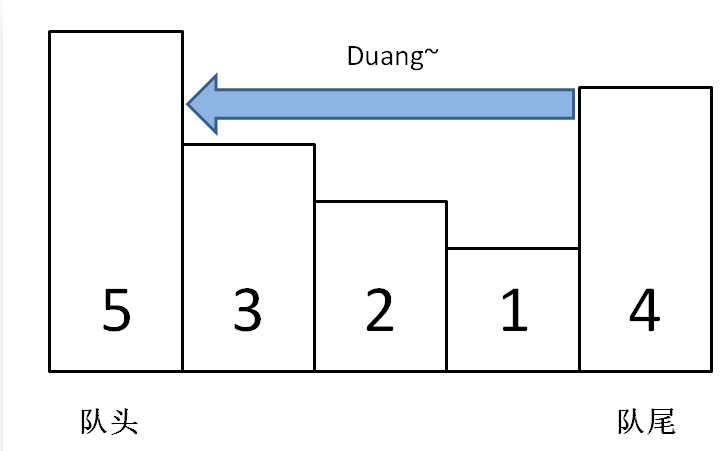
- 首先利用队列这个结构，先进先出（我们可以实现每次让最先进来出去），为什么要变成单调的队列呢？因为我们要的是最大值，我们弄一个递减的队列，每次头都是最大值，我们去判断，如果队列的头的值是我们刚刚窗口最左边的值，我们可以将这个值删除，就不会影响我们向右移动，窗口左边的值影响我们取最大值
入队操作push
- 每次先将前面那些小于要添加的元素的值删除，这样就可以得到一个递增的队列
关于删除，因为只能从头去删除，对于我们这道题，我们什么时候去删除队列的头元素呢
- 我们知道，我们去移动窗口的时候，如果窗口最左边的数字等于我们当前窗口的最大值（单调队列的头节点），那么我们应该去删除头节点的值，如果最左边的数不是我们的最大值，就不需要去删除
Offer39数组中出现次数超过一半的数字
- 用哈希表来统计
- 使用sort，然后找中间+1的数
- 用摩尔投票法
public int majorityElement(int[] nums) { // 我们想寻找的那个众数 int target = 0; // 计数器（类比带电粒子例子中的带电性） int count = 0; for (int i = 0; i < nums.length; i++) { if (count == 0) { // 当计数器为 0 时，假设 nums[i] 就是众数 target = nums[i]; // 众数出现了一次 count = 1; } else if (nums[i] == target) { // 如果遇到的是目标众数，计数器累加 count++; } else { // 如果遇到的不是目标众数，计数器递减 count--; } } // 回想带电粒子的例子 // 此时的 count 必然大于 0，此时的 target 必然就是目标众数 return target; }
扫一扫
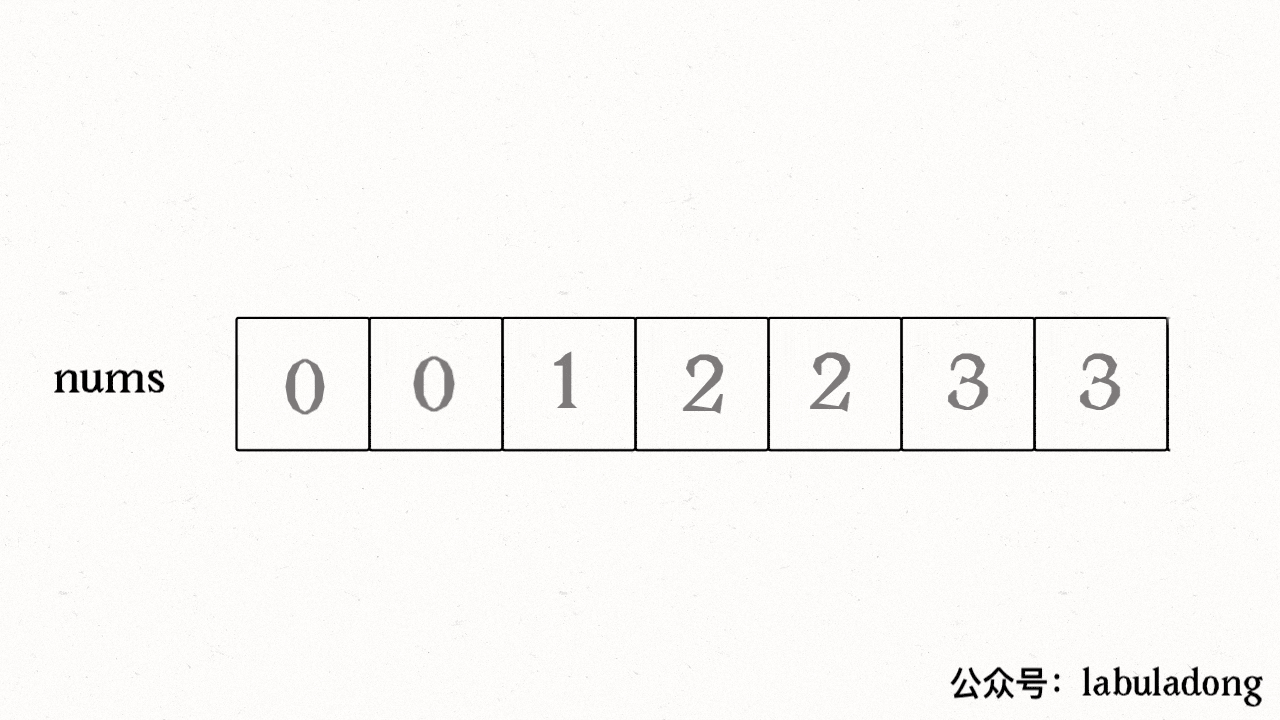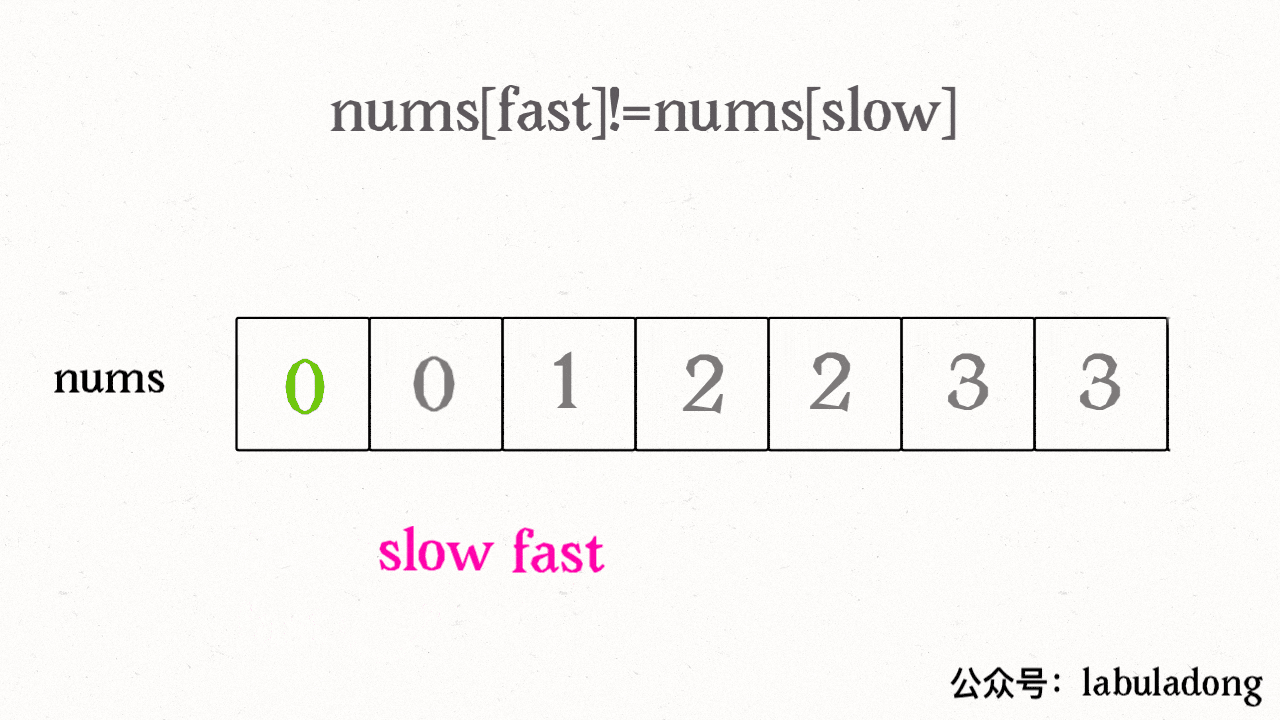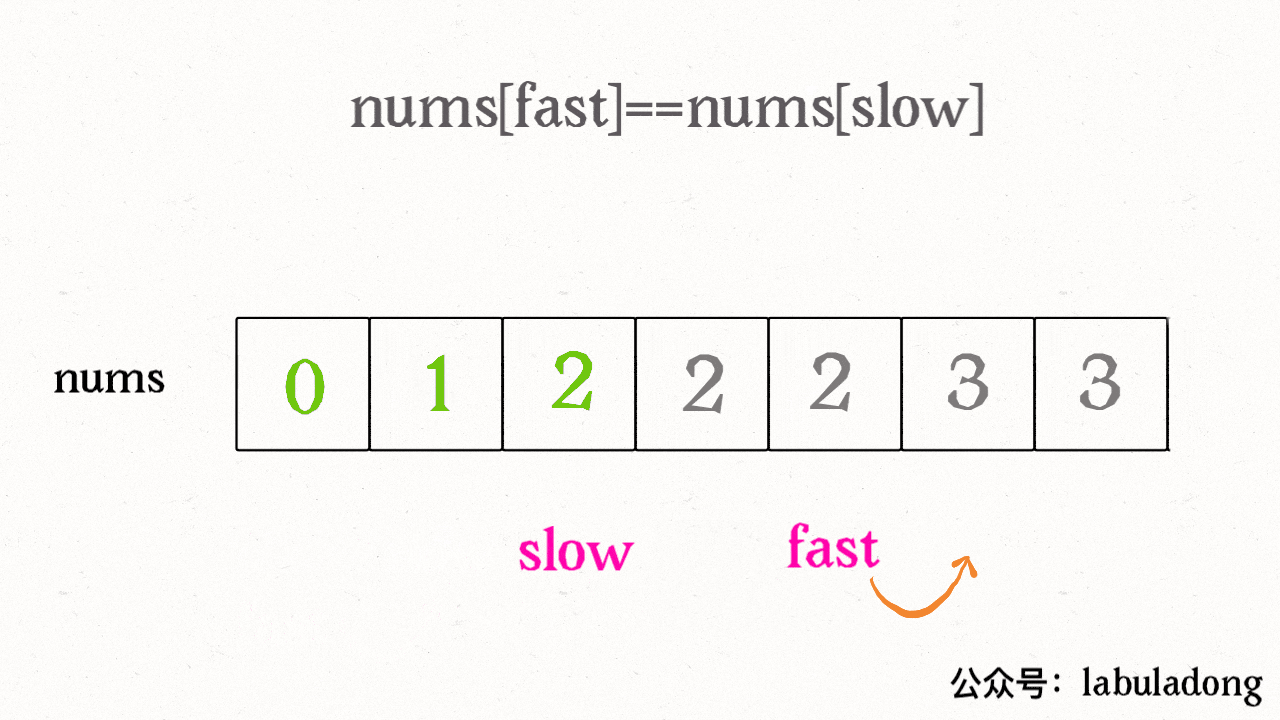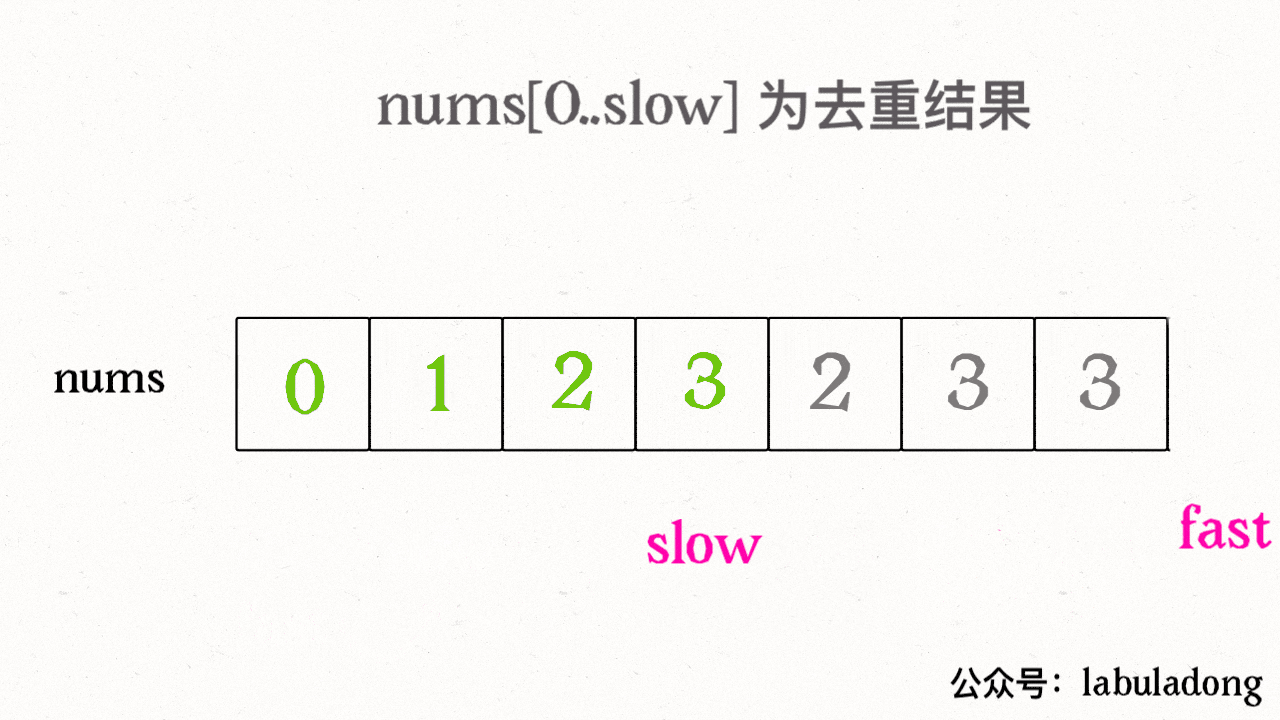
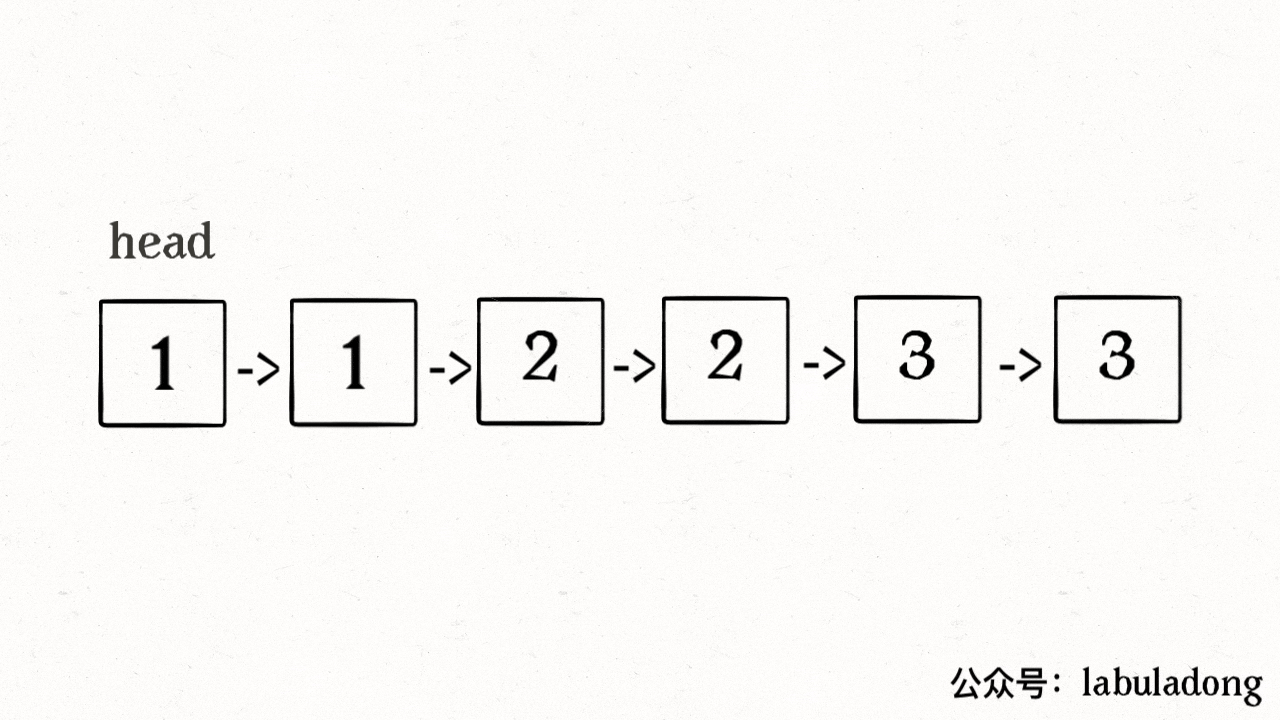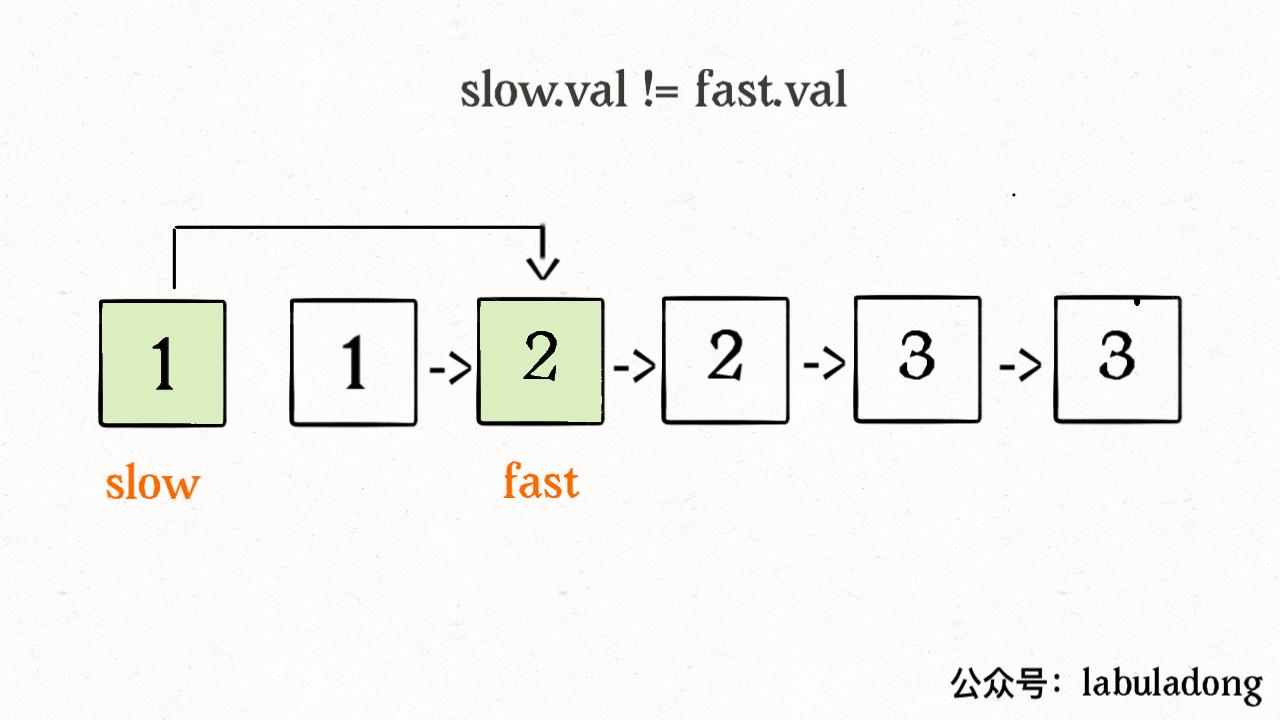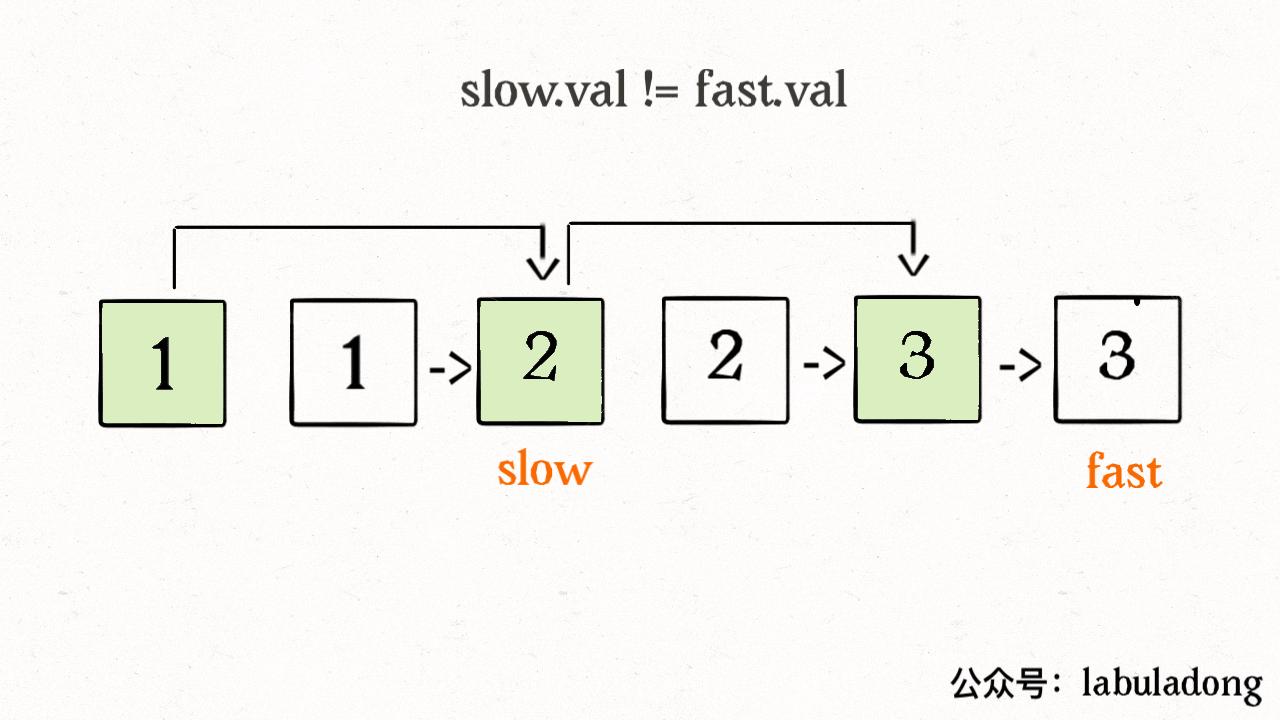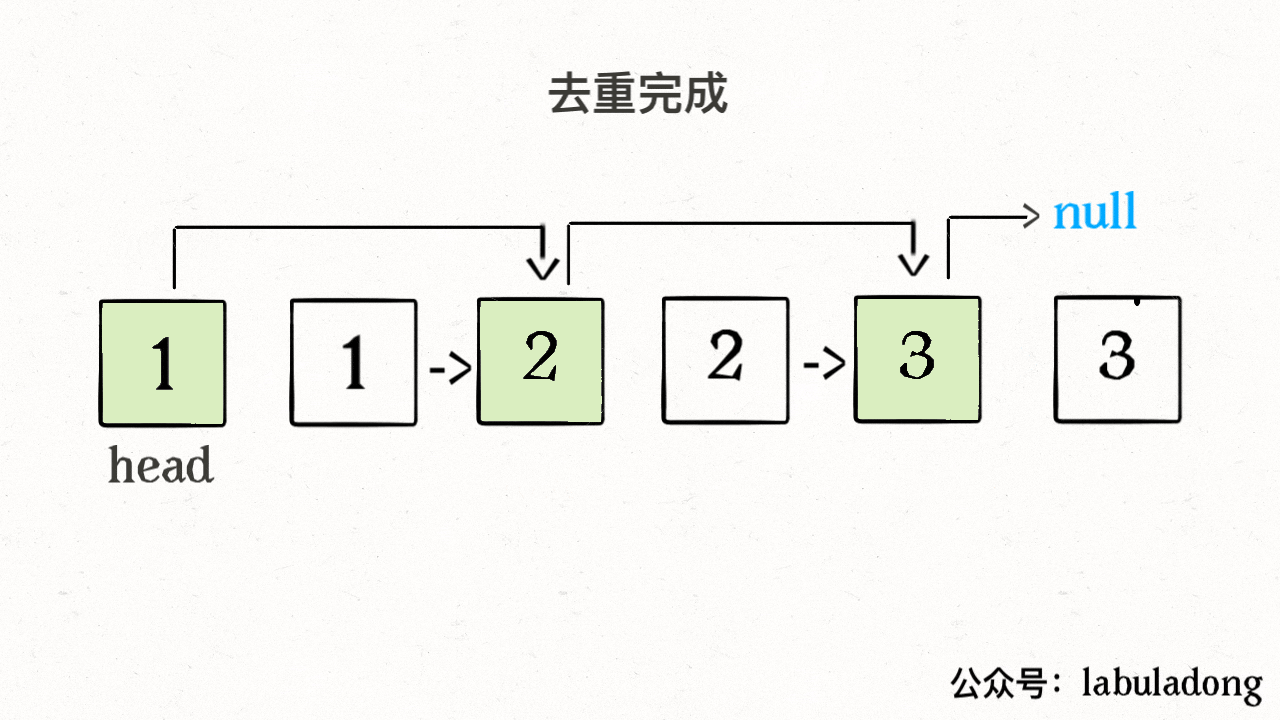
119
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
