我的意思是超级树剖。（树剖多图清晰解释）

P2590 [ZJOI2008]树的统计 题解（bushi）

树剖（重剖）码量较大，不好理解，结合一点基础面向对象的知识分析一下。

部分〇 概念讲解

树剖是把一棵树剖解成几条链，以便像处理序列
一样处理一些树上区间——路径问题的一种算法。

考虑这一点：

• 树上一个节点可以有多个后继， 而链上的一个节点最多只能有一个后继，也就是（a[i] -> a[i+1]），要解决这个矛盾，必须弄清楚一根链形成过程中，末端选择哪个后继点，这也是不同树剖算法的区别。

而重链剖分选择以子树大小（子树节点数）最大的子节点作为后继点。
可以证明，这样的树剖复杂度一般是*(logN)的。网络上证明颇多，这里不再赘述。

部分一 建图

首先建图，是普通的前向星，定义“存图者”：

class Edger{
   //存图者
public:
	int head[N], amtE;
	struct edge{
   
		int to, nex;
	}e[M];
	void addE(int x, int y) {
   
		++amtE;
		e[amtE].to=y; e[amtE].nex=head[x];
		head[x]=amtE;
	}
	void aue(int x, int y) {
   
		addE(x, y), addE(y, x);
	}
}G;
#define allE(x) \
for(int i=G.head[x], y=G.e[i].to; i; i=G.e[i].nex, y=G.e[i].to)
//访问x的所有边。

部分二 剖树

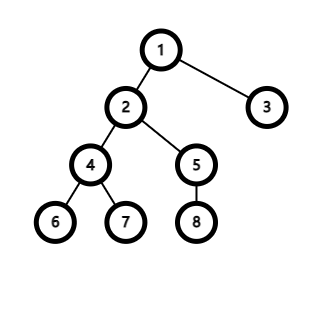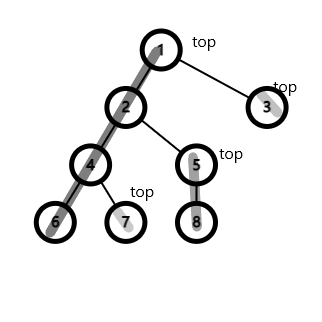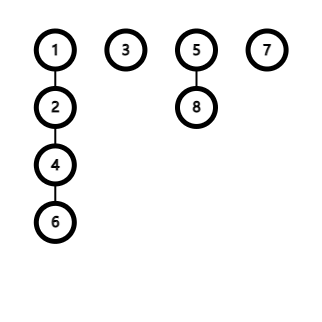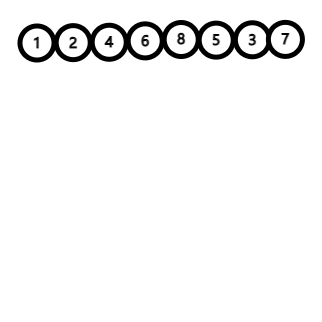
树剖是把一棵树剖解成几条链，以便像处理序列一样处理一些“树上区间”——路径，的一种算法，要实现这个，主要需要两个dfs。

简单解释一下树的链条形状和实现方式：

1. top[x]指向链顶编号(深度最小的点）
2. dfn[x]是x第几个被dfs2访问到，即dfs序，用它充当x在新序列上的编号（可以保证连续）。
3. son[x]是x的si值最大的子节点。
   其他的变量：
   dep[x] 点x的深度
   fa[x] 点x的父节点
   si[x] 点x的子树大小（节点数）
   

namespace ToCutaTree {
   
int t;
int dep[N], fa[N], top[N], dfn[N];//完成树剖后有用的值。
int si[N], son[N];//用于完成树剖的值。
void dfs1(int x, int f) {
   
	fa[x]=f, dep[x]=dep[f]+1, si[x]=1;//显然：赋合理的初值
	allE(x) if(y!=f) {
   
		dfs1(y, x); si[x]+=si[y];//将所有子节点的个数记录下来。
		if(si[y]>si[son[x]]) son[x]=y;
	}
}

显然dfs1非常简单， 就是求出可以直接求的一些值。

然后是dfs2。
这里开始把树的链条撕 对应到一个序列上：有一些难点：

1. 首先要明白，dfs是 在x上就做x上的事。
2. 求top[x]，根据重剖的定义， 只有当x是fa[x]的son（son[fa[x]]）时，才能将fa[x]这条重链连向x， 否则x自己为新重链的链顶。
3. 上面说到，一条链上的dfn[x]必须保持它的连续性。（使新的序列中属同链的点紧挨在一起。） 所以一旦x有son[x]（非叶子节点），则必须优先访问son[x]（而非其他的非son子节点）。

void dfs2(int x, int f) {
   
	top[x]=x, dfn[x]=++t, v[t]=a[x];
	if(x==son[f]) top[x]=top[f];//1.
	if(son[x]) dfs2(son[x],x);//2.
	allE(x) if(y!=f&&y!=son[x]) dfs2(y,x);//访问中除去son[x]（已访问。）
}
void treecut() {
   
	dfs1(1, 0); t=0;
	dfs2(1, 0);
}
}

部分三 线段树

讲解不再赘述。
注意维护的是新的虚拟序列v[]

class segTree{
   //定义线段树类
#define makmid \
int mid=(L+R)>>1;//快速算mid
#define ls (p<<1)
#define rs ((p<<1)+1)
	int tr[N<<2], mx[N<<2];
	void pushup(int p) {
   
		tr[p]=tr[ls]+tr[rs];
		mx[p]=max(mx[ls],mx[rs]);
	}

	void cha(int p, int L, int R, int x, int t) {
   
		if(L==R) {
    tr[p]=mx[p]=t; return; }
		else {
    makmid;
			if(x<=mid) cha(ls,L,mid,x,t