时间与空间复杂度

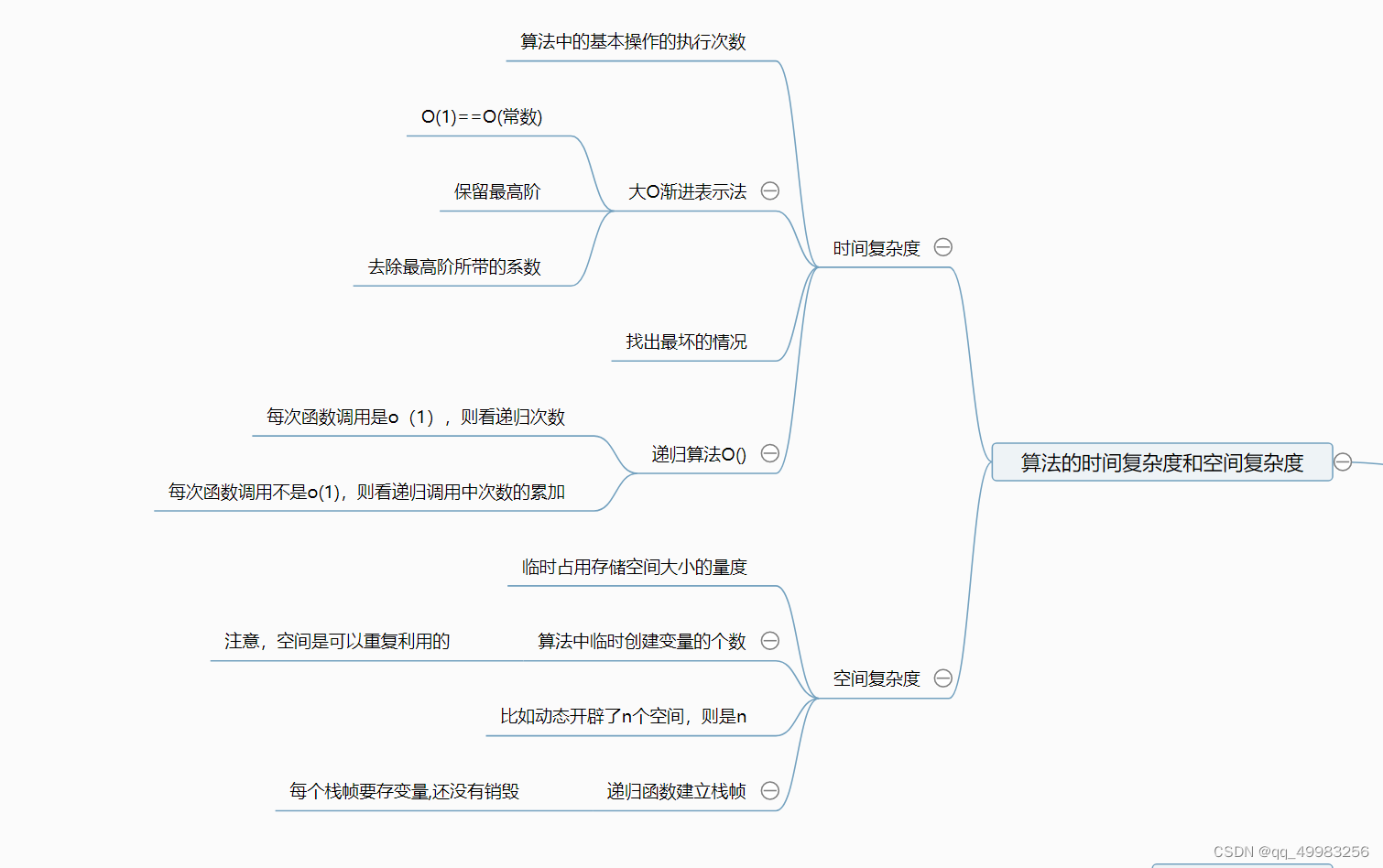
时间复杂度的概念
时间复杂度的定义：在计算机科学中，算法的时间复杂度是一个函数。算法中的基本操作的执行次数，为算法的时间复杂度。

即:找到某条基本语句与问题规模N之间的数学表达式，就是算出了该算法的时间复杂度

本质是数学问题

若

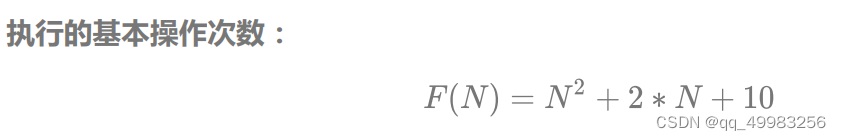
实际中我们计算时间复杂度时，我们其实并不一定要计算精确的执行次数，而只需要大概执行次数，那么我们使用大O的渐进表示法

有些算法的时间复杂度存在最好、平均和最坏情况：
最坏情况：任意输入规模的最大运行次数(上界)
平均情况：任意输入规模的期望运行次数
最好情况：任意输入规模的最小运行次数(下界)
例如：在一个长度为N数组中搜索一个数据x---查找算法
最好情况：1次找到
最坏情况：N次找到
平均情况：N/2次找到
默认在实际中一般情况关注的是算法的最坏运行情况，所以数组中搜索数据时间复杂度为O(N)
 

举个例子

二分查找（写的时候注意边界情况）---为了更加形象，我假设我已经知道了待查找元素得位置,那么即可实现二分查找的反过程

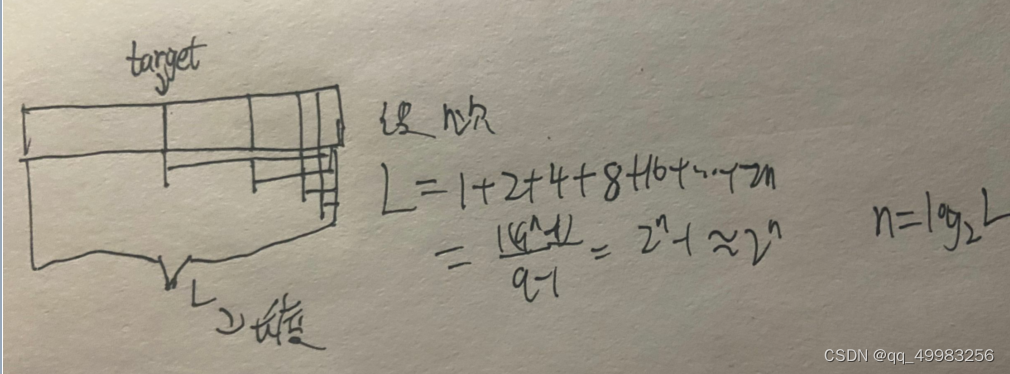
 2的30次方==10亿,二分查找下只需30次,从头开始找10亿次

// 计算阶乘递归Fac的时间复杂度？
long long Fac(size_t N)
{
    if(0 == N)
    return 1;
    return Fac(N-1)*N;
}
O(n)---------------层层递归，画图分析比较好理解
像上面这种普通情况,每次调用次数均为1,调用N次
long long Fac(size_t N)
{
    if(0 == N)
    return 1;
    for (i=0;i<N;i++)
    {
        //打印i
    }
    return Fac(N-1)*N;
}
//先算for循环,第一次进去N-1次，第二次N-2......最后1
等差数列,n方
//后面return Fac,是O(n)，相较于n方可忽略

// 计算斐波那契递归Fib的时间复杂度？
long long Fib(size_t N)
{
    if(N < 3)
        return 1;
    return Fib(N-1) + Fib(N-2);
}
//大约从N，开始减,N层。
//低层是上层的两倍
 

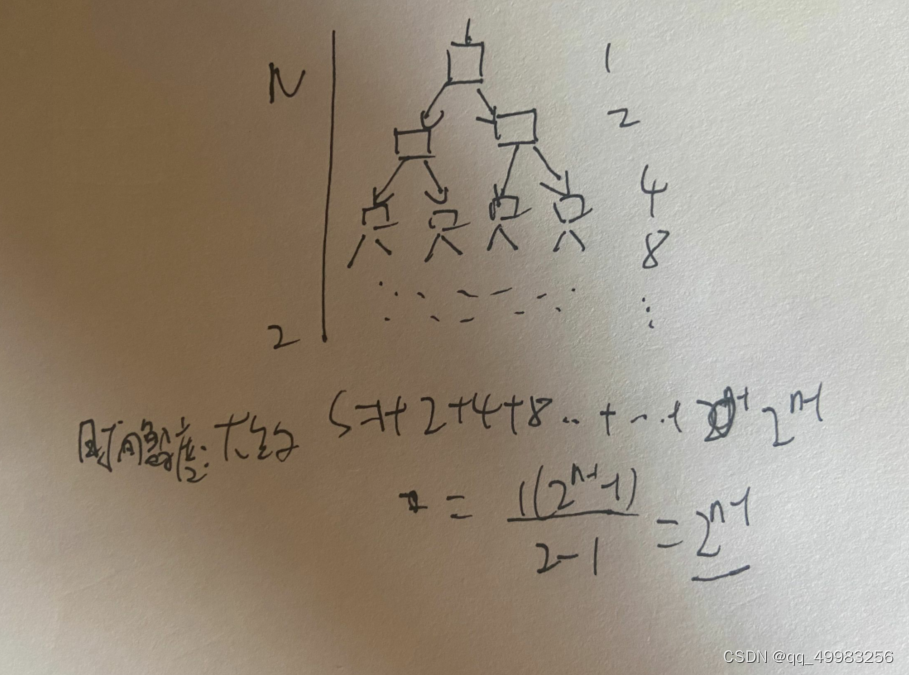
空间复杂度

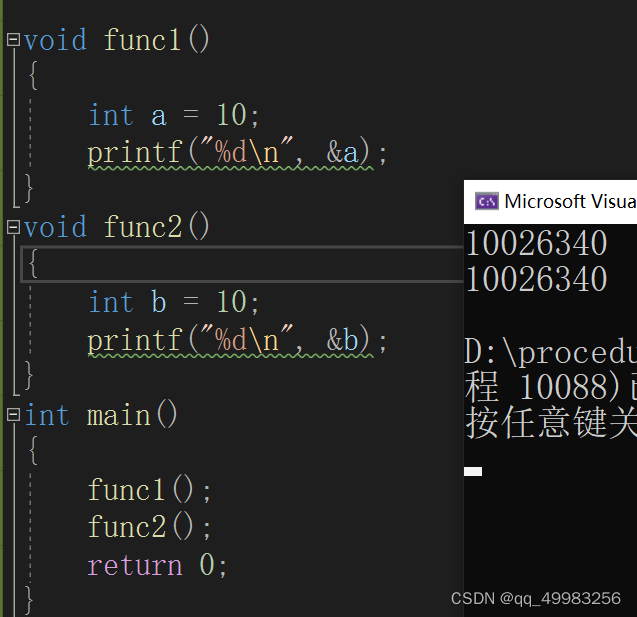
空间复杂度也是一个数学表达式，是对一个算法在运行过程中临时占用存储空间大小的量度 。空间复杂度算的是变量的个数。
注意：函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了，因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定

注意点:

a =malloc(sizeof(int*)*20)----o(1)

a =malloc(sizeof(int*)*n)----o(n)

重点

// 计算斐波那契递归Fib的空间复杂度？---O（N）
long long Fib(size_t N)
{
    if(N < 3)
    return 1;
    return Fib(N-1) + Fib(N-2);
}

注意，空间是可以重复利用的

右侧图像

像递归调用过程 

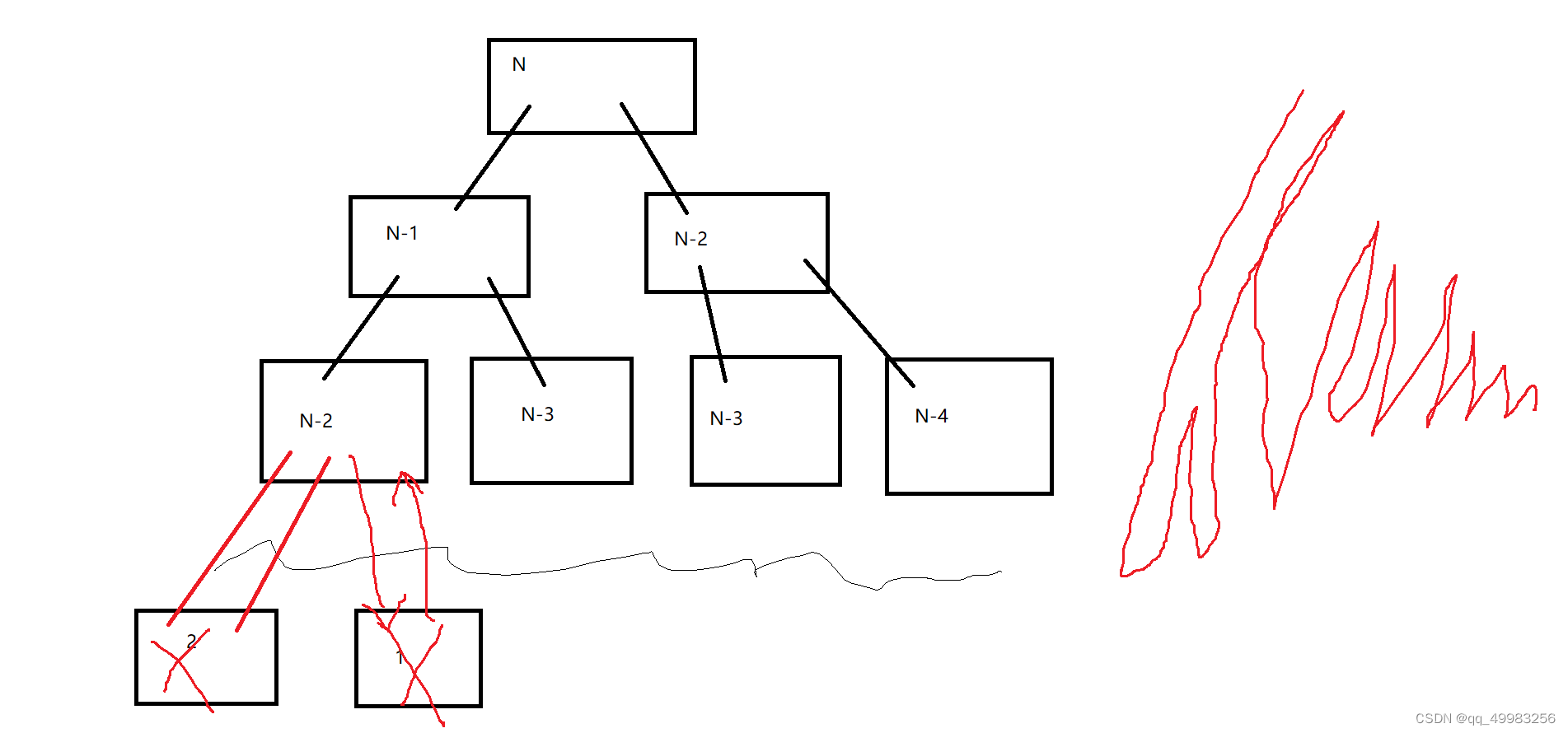
每一层地址是相同的，栈是向下生长的。