P8819 [CSP-S 2022] 星战 题解

P8819 [CSP-S 2022] 星战

题面：

题目描述

在这一轮的星际战争中，我方在宇宙中建立了 $n$ 个据点，以 $m$ 个单向虫洞连接。我们把终点为据点 $u$ 的所有虫洞归为据点 $u$ 的虫洞。

战火纷飞之中这些虫洞很难长久存在，敌人的打击随时可能到来。这些打击中的有效打击可以分为两类：

1. 敌人会摧毁某个虫洞，这会使它连接的两个据点无法再通过这个虫洞直接到达，但这样的打击无法摧毁它连接的两个据点。
2. 敌人会摧毁某个据点，由于虫洞的主要技术集中在出口处，这会导致该据点的所有还未被摧毁的虫洞被一同摧毁。而从这个据点出发的虫洞则不会摧毁。

注意：摧毁只会导致虫洞不可用，而不会消除它的存在。

为了抗击敌人并维护各部队和各据点之间的联系，我方发展出了两种特种部队负责修复虫洞：

• A 型特种部队则可以将某个特定的虫洞修复。
• B 型特种部队可以将某据点的所有损坏的虫洞修复。

考虑到敌人打击的特点，我方并未在据点上储备过多的战略物资。因此只要这个据点的某一条虫洞被修复，处于可用状态，那么这个据点也是可用的。

我方掌握了一种苛刻的空间特性，利用这一特性我方战舰可以沿着虫洞瞬移到敌方阵营，实现精确打击。

为了把握发动反攻的最佳时机，指挥部必须关注战场上的所有变化，为了寻找一个能够进行反攻的时刻。总指挥认为：

• 如果从我方的任何据点出发，在选择了合适的路线的前提下，可以进行无限次的虫洞穿梭（可以多次经过同一据点或同一虫洞），那么这个据点就可以实现反击。
• 为了使虫洞穿梭的过程连续，尽量减少战舰在据点切换虫洞时的质能损耗，当且仅当只有一个从该据点出发的虫洞可用时，这个据点可以实现连续穿梭。
• 如果我方所有据点都可以实现反击，也都可以实现连续穿梭，那么这个时刻就是一个绝佳的反攻时刻。

总司令为你下达命令，要求你根据战场上实时反馈的信息，迅速告诉他当前的时刻是否能够进行一次反攻。

输入格式

输入的第一行包含两个正整数 $n,m$。

接下来 $m$ 行每行两个数 $u,v$，表示一个从据点 $u$ 出发到据点 $v$ 的虫洞。保证 $u\ne v$，保证不会有两条相同的虫洞。初始时所有的虫洞和据点都是完好的。

接下来一行一个正整数 $q$ 表示询问个数。

接下来 $q$ 行每行表示一次询问或操作。首先读入一个正整数 $t$ 表示指令类型：

• 若 $t=1$，接下来两个整数 $u,v$ 表示敌人摧毁了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且未被摧毁。
• 若 $t=2$，接下来一个整数 $u$ 表示敌人摧毁了据点 $u$。如果该据点的虫洞已全部被摧毁，那么这次袭击不会有任何效果。
• 若 $t=3$，接下来两个整数 $u,v$ 表示我方修复了从据点 $u$ 出发到据点 $v$ 的虫洞。保证该虫洞存在且被摧毁。
• 若 $t=4$，接下来一个整数 $u$ 表示我方修复了据点 $u$。如果该据点没有被摧毁的虫洞，那么这次修复不会有任何效果。

在每次指令执行之后，你需要判断能否进行一次反攻。如果能则输出 YES 否则输出 NO。

输出格式

输出一共 $q$ 行。对于每个指令，输出这个指令执行后能否进行反攻。

样例 #1

样例输入 #1

3 6
2 3
2 1
1 2
1 3
3 1
3 2
11
1 3 2
1 2 3
1 1 3
1 1 2
3 1 3
3 3 2
2 3
1 3 1
3 1 3
4 2
1 3 2

样例输出 #1

NO
NO
YES
NO
YES
NO
NO
NO
YES
NO
NO

提示

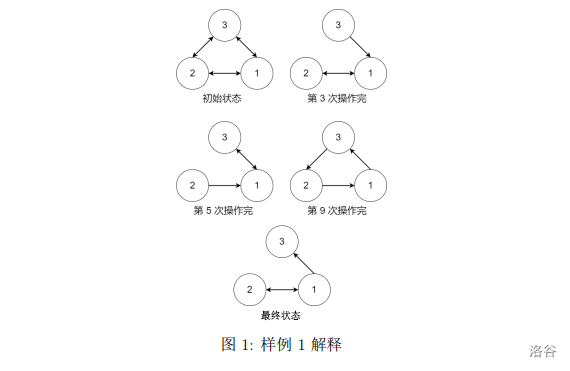
【样例解释 #1】

虫洞状态可以参考下面的图片, 图中的边表示存在且未被摧毁的虫洞：

【样例 #2】

见附件中的 galaxy/galaxy2.in 与 galaxy/galaxy2.ans。

【样例 #3】

见附件中的 galaxy/galaxy3.in 与 galaxy/galaxy3.ans。

【样例 #4】

见附件中的 galaxy/galaxy4.in 与 galaxy/galaxy4.ans。

【数据范围】

对于所有数据保证：$1\le n\le 5\times {10}^5$，$1\le m\le 5\times {10}^5$，$1\le q\le 5\times {10}^5$。

测试点	$n\le$	$m\le$	$q\le$	特殊限制
$1\sim 3$	$10$	$20$	$50$	无
$4\sim 8$	${10}^3$	${10}^4$	${10}^3$	无
$9\sim 10$	$5\times {10}^5$	$5\times {10}^5$	$5\times {10}^5$	保证没有 $t=2$ 和 $t=4$ 的情况
$11\sim 12$	$5\times {10}^5$	$5\times {10}^5$	$5\times {10}^5$	保证没有 $t=4$ 的情况
$13\sim 16$	${10}^5$	$5\times {10}^5$	$5\times {10}^5$	无
$17\sim 20$	$5\times {10}^5$	$5\times 10^5$	$5\times {10}^5$	无

连续穿梭~~~每个点只能有一条出边。

简化题意就是：给定一个图，支持 删边 ~ 删点 ~ 加（被删的）边 ~ 加（被删的）点 操作，询问是否可以构成一个内向基环树。

一看就很不好做，但是询问只有 $YES$ 和 $NO$。

这个时候，非确定性算法就很可能隐藏其中。

我们知道一个图是内向基环树的必要条件是 ${\mathrm{deg}}_{\text{out}}=n$

那么，非确定性算法就是用必要条件来保证充分性！

本题就是一个重要非确定性算法——和哈希（sumhash）

我们求 $\sum _i{\mathrm{deg}}_i=n$，但这样很容易出问题，很多情况可以 $\sum _i{\mathrm{deg}}_i=n$。

那么，我们就不要让每个点的出度为 $1$ 了，我们把出度随机变宽。

也就是我们将每个点的出度随机赋值，一个图是内向基环树的必要条件就是 $\sum {\mathrm{deg}}_{out}=\sum w_i$

然鹅，出度不易维护，所以我们换成入度！入度和出度在内向基环树是显然等价的

那么，我们就只用判断这个 $\sum {\mathrm{deg}}_{in}=\sum w_i$ 条件就可以了。

我们用三个数组维护操作：

$r_i$ 表示 $i$ 当前入度，$g_i$ 表示 $i$ 原始入度，有：

1. $(u,v)$ 失活，$r_v\leftarrow r_u-1$

2. $v$ 失活，$r_v\leftarrow 0$

3. $(u,v)$ 复活，$r_v\leftarrow r_u+1$

4. $v$ 复活， $r_v\leftarrow g_v$

只要实现上面的操作，就可以通过此题。

AC-code:

#include<bits/stdc++.h>
using namespace std;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
void wt(int x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}
const int N = 5e5+5;
int n,m,g[N],r[N],w[N];
mt19937_64 rng(chrono::steady_clock::now().time_since_epoch().count());
template<typename T>
T rnr(T l, T r){
	return l+(unsigned long long)rng()%(r-l+1);
}

signed main() {
	n = rd(),m = rd();
	for(int i = 1;i<=n;i++) w[i] = rnr((int)1,(int)(1e10));
	int tar = accumulate(w + 1,w + n + 1,0LL);
	int now = 0;
	for(int i = 1;i<=m;i++) {
		int u = rd(),v = rd();
		r[v] += w[u];
		g[v] = r[v];
		now += w[u];
 	}
	int q = rd();
	while(q--) {
		int op = rd(),u,v;
		switch(op) {
			case 1:
				u = rd(),v = rd();
				r[v] -= w[u];
				now -= w[u];
				break;
			case 2:
				v = rd();
				now -= r[v];
				r[v] = 0;
				break;
			case 3:
				u = rd(),v = rd();
				r[v] += w[u];
				now += w[u];
				break;
			case 4:
				v = rd();
				now += g[v] - r[v];
				r[v] = g[v];
				break;
			default:
				puts("Error");
				exit(0);
				break;
		}
		puts((now == tar) ? "YES" : "NO");
	}
	
	return 0;
}