P3960 [NOIP2017 提高组] 列队 题解

P3960 [NOIP2017 提高组] 列队

题面：

题目背景

NOIP2017 D2T3

题目描述

Sylvia 是一个热爱学习的女孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有 $n\times m$ 名学生，方阵的行数为 $n$，列数为 $m$。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中 的学生从 $1$ 到 $n\times m$ 编上了号码（参见后面的样例）。即：初始时，第 $i$ 行第 $j$ 列 的学生的编号是 $(i-1)\times m+j$。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天 中，一共发生了 $q$ 件这样的离队事件。每一次离队事件可以用数对 $(x,y)(1\le x\le n,1\le y\le m)$ >描述，表示第 $x$ 行第 $y$ 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达 这样的两条指令：

1. 向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条 指令之后，空位在第 $x$ 行第 $m$ 列。
2. 向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条 指令之后，空位在第 $n$ 行第 $m$ 列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后， 下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 $n$ 行 第 $m$ 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学 的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后 方阵中同学的编号可能是乱序的。

输入格式

输入共 $q+1$ 行。

第一行包含 $3$ 个用空格分隔的正整数 $n,m,q$，表示方阵大小是 $n$ 行 $m$ 列，一共发 生了 $q$ 次事件。

接下来 $q$ 行按照事件发生顺序描述了 $q$ 件事件。每一行是两个整数 $x,y$，用一个空 格分隔，表示这个离队事件中离队的学生当时排在第 $x$ 行第 $y$ 列。

输出格式

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学生的编号。

样例 #1

样例输入 #1

2 2 3 
1 1 
2 2 
1 2

样例输出 #1

1
1
4

提示

【输入输出样例 $1$ 说明】

$$\begin{array}{ccccccccc}\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}& 2\\ 3& 4\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& \\ 3& 4\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 4\\ 3& \end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 4\\ 3& 1\end{array}\right]\\ \left[\begin{array}{cc}2& 4\\ 3& 1\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 4\\ 3& \end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 4\\ 3& \end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 4\\ 3& \end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 4\\ 3& 1\end{array}\right]\\ \left[\begin{array}{cc}2& 4\\ 3& 1\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& \\ 3& 1\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& \\ 3& 1\end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 1\\ 3& \end{array}\right]& \Rightarrow & \left[\begin{array}{cc}2& 1\\ 3& 4\end{array}\right]\end{array}$$

列队的过程如上图所示，每一行描述了一个事件。 在第一个事件中，编号为 $1$ 的同学离队，这时空位在第一行第一列。接着所有同学 向左标齐，这时编号为 $2$ 的同学向左移动一步，空位移动到第一行第二列。然后所有同 学向上标齐，这时编号为 $4$ 的同学向上一步，这时空位移动到第二行第二列。最后编号为 $1$ 的同学返回填补到空位中。

【数据规模与约定】

测试点编号	$n$	$m$	$q$	其他约定
$1\sim 6$	$\le 10^3$	$\le 10^3$	$\le 500$	无
$7\sim 10$	$\le 5\times 10^4$	$\le 5\times 10^4$	$\le 500$	无
$11\sim 12$	$=1$	$\le 10^5$	$\le 10^5$	所有事件 $x=1$
$13\sim 14$	$=1$	$\le 3\times 10^5$	$\le 3\times 10^5$	所有事件 $x=1$
$15\sim 16$	$\le 3\times 10^5$	$\le 3\times 10^5$	$\le 3\times 10^5$	所有事件 $x=1$
$17\sim 18$	$\le 10^5$	$\le 10^5$	$\le 10^5$	无
$19\sim 20$	$\le 3\times 10^5$	$\le 3\times 10^5$	$\le 3\times 10^5$	无

数据保证每一个事件满足 $1\le x\le n,1\le y\le m$。

填坑了，2024.7 动态开点线段树熟练运用

除了保险没全开long long导致只拿了 $55$ 分，基本上是一遍过

线段树上二分是关键！

我们想到模拟 $n$ 行队列，

但是一个致命的问题摆在我们面前：指令 $2$ 怎么实现？

我们试着模拟一下过程，如图：

如果有 $(x,y)$ 要离队，

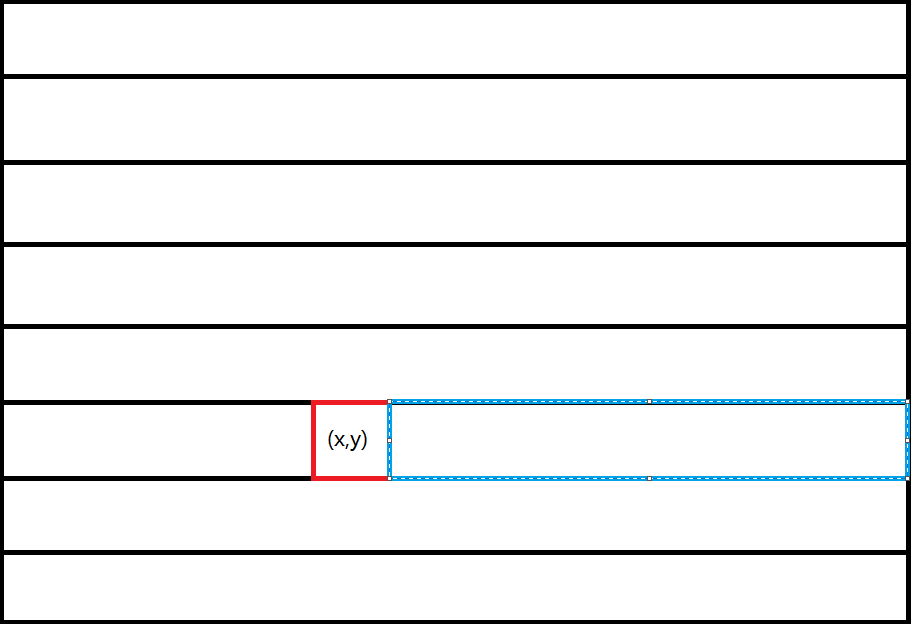
那么他所在行的 $(x,y+1\sim n)$ 要补上去(即蓝色部分)

此时队尾（黄色处）出现空缺，那么 $m$ 列的 $(x+1\sim n,m)$ 要顶上去（即红色部分），且这个时候离队归队（绿色部分）了：

---

我们可以看到，如果把最后一列也单独开一个线段树便可以维护了，

可能还是有些人会一头雾水，在此，我把 每个线段树维护的队列标注出来：

---

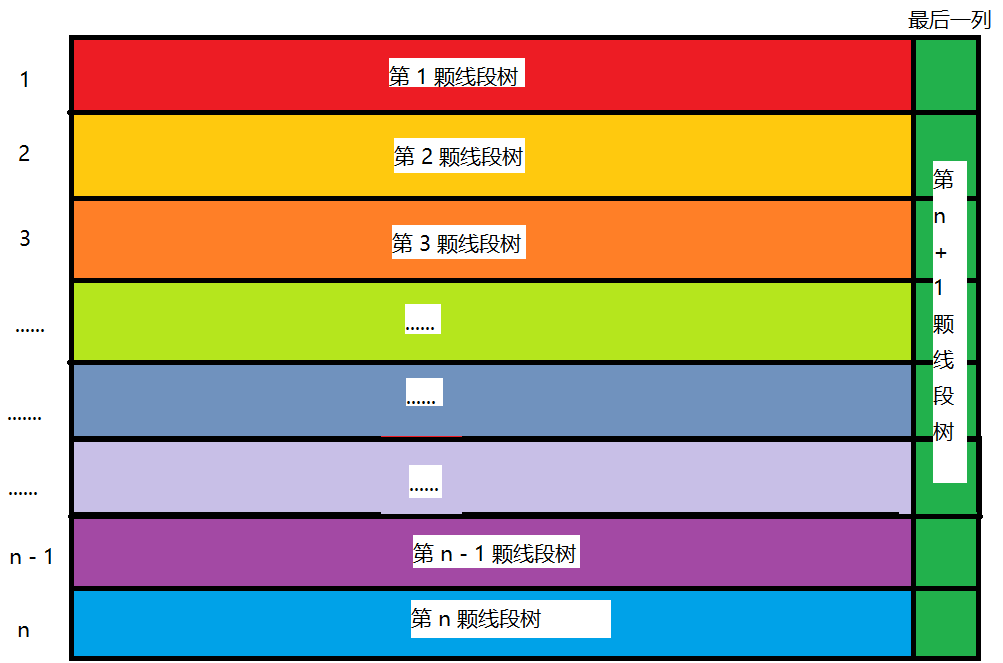
考察操作实现：

以下的“取出”操作表示：“先查询出来后删除”

当 $(x,y)$ 的同学离队时，分讨：

1. 如果 $y=m$，
   我们将 第 $n+1$ 颗线段树（维护的是最后一列）中的 第 $x$ 个元素取出（节点大小和元素值设为 $0$），
   然后，以队列第 $n$ 个元素添加进 第 $n+1$ 颗线段树。

2. 如果 $y<m$
   我们将 第 $x$ 颗线段树中 第 $y$ 个元素 取出,
   然后执行指令 $1$，我们将第 $n+1$ 颗线段树中 第 $x$ 个元素 取出，以队列第 $m-1$ 个元素（队尾）添加到 $x$ 颗线段树中
   最后执行指令 $2$，我们将在第一步取出的元素在第 $n+1$ 颗线段树上以 $n$ 个元素（队尾）添加到队列

本题就这样解决了！…吗？

---

动态开点线段树的细节：
直接 build()建点完全是痴人说梦！

如果这样建点，一共要建 $3\times 10^5\times 3\times 10^5=9\times 10^{10}$ ，空间爆炸！

所以我们大部分点都是虚点（本文指不存在的点）

但是他们在线段树上确确实实占了空间和大小！

所以初始化需要和建点结合！

并且二分的时候，是依靠左右儿子的大小二分的。

所以我们必须在访问之前建出左右儿子，且push_up()

由于询问有 $q\in 3\times 10^5$ ，加上原队列长度 $n/m\in 3\times 10^5$，合计 $6\times 10^5$，以这个为大小存点。

根据每个线段树的不同，初始化的元素值也需要计算出来！

最后的问题：为什么初始化的时候能直接计算出来元素值呢？

因为没有初始化的节点说明没有修改过，所以里面的元素是可以推出的，

后面来了一些点，这些点在初始化的时候大抵根本不存在这个列队中，但是这些点很快被我们赋予的权值给顶掉了，所以没有任何影响！

当这些都完成的时候，此题就完美 $AC$ 了！

AC-code：

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
#define int long long
int rd() {
	int x = 0, w = 1;
	char ch = 0;
	while (ch < '0' || ch > '9') {
		if (ch == '-') w = -1;
		ch = getchar();
	}
	while (ch >= '0' && ch <= '9') {
		x = x * 10 + (ch - '0');
		ch = getchar();
	}
	return x * w;
}
template<class T = ll>
void wt(T x) {
	static int sta[35];
	int f = 1;
	if(x < 0) f = -1,x *= f;
	int top = 0;
	do {
		sta[top++] = x % 10, x /= 10;
	} while (x);
	if(f == -1) putchar('-');
	while (top) putchar(sta[--top] + 48);
}

const int N = 3e5+5,O = 6e5 + 5;
int n,m,q;
int rt[N];
namespace sgt{
int ls[N * 50],rs[N * 50];
int sz[N * 50];
ll val[N * 50],cnt;
#define mid ((pl + pr) >> 1)
void push_up(int p) {sz[p] = sz[ls[p]] + sz[rs[p]];}
void getnode(int &p,int pl,int pr,int o) {
	if(!p) {
		p = ++cnt;
		sz[p] = (pr - pl + 1);
		if(pl == pr && o == n + 1) val[p] = pl * m;
 		else if(pl == pr) val[p] = (o - 1) * m + pl; 
	}
}
void update(int &p,int pl,int pr,int k,int upd,int o) {
	getnode(p,pl,pr,o);
	if(pl ^ pr) getnode(ls[p],pl,mid,o);
	if(pl ^ pr) getnode(rs[p],mid+1,pr,o);
	if(pl ^ pr) push_up(p);
	if(pl == pr) {
		sz[p] = (upd > 0) ? 1 : 0;
		val[p] = (upd > 0) ? upd : 0;
		return;
	}
	if(k <= sz[ls[p]]) update(ls[p],pl,mid,k,upd,o);
	else update(rs[p],mid+1,pr,k - sz[ls[p]],upd,o);
	push_up(p);
}

int query(int &p,int pl,int pr,int k,int o) {
	getnode(p,pl,pr,o);
	if(pl ^ pr) getnode(ls[p],pl,mid,o);
	if(pl ^ pr) getnode(rs[p],mid+1,pr,o);
	if(pl ^ pr) push_up(p);
	if(pl == pr) return val[p];
	if(k <= sz[ls[p]]) return query(ls[p],pl,mid,k,o);
	else return query(rs[p],mid+1,pr,k - sz[ls[p]],o);
}
}

// 1 ~ n 是 第1行到第n行的队列
// n + 1 是 第m列的队列

signed main() {
	n = rd(),m = rd(),q = rd();
	while(q--) {
		int x = rd(),y = rd(),re = 0,tl = 0;
		if(y == m) {
			re = sgt::query(rt[n + 1],1,O,x,n + 1);
			sgt::update(rt[n + 1],1,O,x,0,n + 1);
			sgt::update(rt[n + 1],1,O,n,re,n + 1);
			wt(re);putchar('\n');
		}else {
			re = sgt::query(rt[x],1,O,y,x);
			sgt::update(rt[x],1,O,y,0,x); // 删除 (x,y) -> line x
			tl = sgt::query(rt[n + 1],1,O,x,n + 1); 
			sgt::update(rt[n + 1],1,O,x,0,n + 1);// 删除 (x,m) -> col m
			sgt::update(rt[x],1,O,m-1,tl,x);//添加 (x,m) -> line x
			sgt::update(rt[n + 1],1,O,n,re,n + 1);//添加 (x,y) -> col m
			wt(re),putchar('\n');
		}
	}
	
	return 0;
}