一. 什么是汉诺塔?
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。
大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。
大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。
规定:在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。
二. 分析
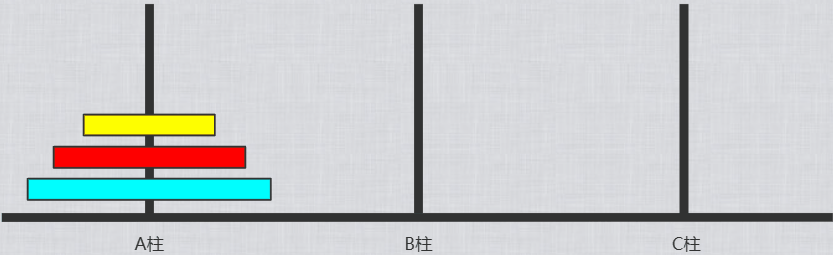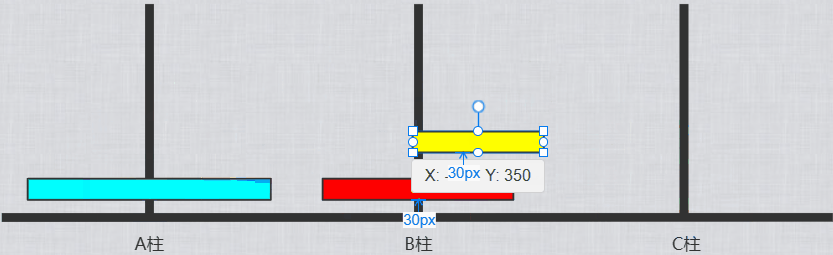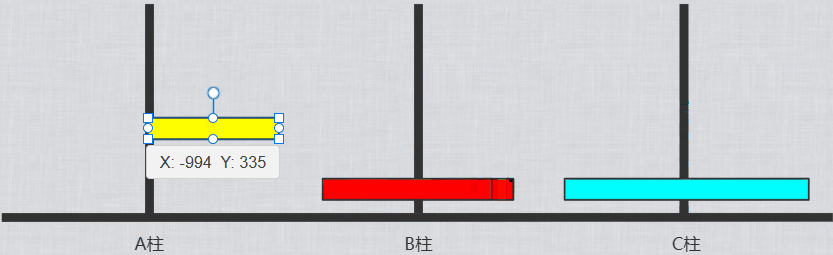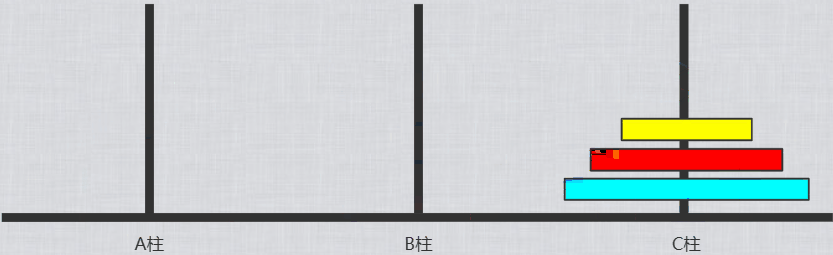
若只有1个圆盘时,从A柱移动到C柱,需要1步。2个圆盘时,则需要3步。3个圆盘时,则需要7步。
1.第1个圆盘从A-------->C
2.第2个圆盘从A-------->B
3.第1个圆盘从C-------->B
4.第3个圆盘从A-------->C
5.第1个圆盘从B-------->A
6.第2个圆盘从B-------->C
7.第1个圆盘从A-------->C
不难看出,当有n个圆盘时,汉诺塔步数的规律是2^n-1。那么当有64个圆盘时就需要2^64-1步。
通过分析我们可以将其分为三个步骤:
1.通过递归将A柱的n-1个圆盘从A柱移动到B柱(C为工具柱)
2.将A柱最后1个圆盘移动到C柱
3.此时B柱有n-1个圆盘,C柱有1个圆盘。递归将B柱上的圆盘移动到C(A为工具柱)
三. 代码实现
#include <stdio.h>
int step = 0;//步数
//移动一个圆盘
void Move(char a,char c,int n) {
printf("把第%d个圆盘从%c ---> %c\n",n,a,c);
step++;
}
void Hanoi(char a,char b,char c,int n) {
if (n != 1) {
Hanoi(a, c, b, n - 1);//1.当A有n个圆盘时将n-1个圆盘,借助C,移至到B
Move(a, c, n);//2.将A剩余的最后1个圆盘移至C
Hanoi(b, a, c, n - 1);//3.B剩余n-1个圆盘,借助A,移至C
}
else {
Move(a, c, n);//若有1个圆盘,直接将圆盘从A移动到C(递归出口)
}
}
void main() {
int n = 0;
printf("请输入汉诺塔的圆盘数:");
scanf("%d",&n);
Hanoi('a','b','c',n);
printf("共走了%d步",step);
}运行结果:


四. 总结
汉诺塔是经典的递归题,关键还是要理解递归思想,还有,只需要关心自己的任务,分派出去的任务只用关心它最后的结果,而执行过程则不要去过多地关注。
关于C语言实现汉诺塔的讲解到这里就结束了,如果有什么疑问的地方欢迎留在评论区,谢谢支持~









 本文详细介绍了汉诺塔问题的起源、分析和解决步骤,重点阐述了利用递归思想解决64个圆盘的汉诺塔问题。通过C语言代码展示了如何实现移动操作,并提供了具体的运行结果。文章强调理解递归和关注自身任务在解决问题中的重要性。
本文详细介绍了汉诺塔问题的起源、分析和解决步骤,重点阐述了利用递归思想解决64个圆盘的汉诺塔问题。通过C语言代码展示了如何实现移动操作,并提供了具体的运行结果。文章强调理解递归和关注自身任务在解决问题中的重要性。

















 1039
1039

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










