排序-插入排序

插入排序（Insertion Sort）是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在小规模或者部分已排序的数据集上表现良好。

插入排序的特点包括：

1. 时间复杂度：

   • 最好情况（输入数组已经是排序好的）：O(n)，此时只需遍历数组一次，无需进行内部的插入交换。
   • 平均情况和最坏情况（数组完全逆序）：O(n^2)，因为每插入一个新元素都需要与它之前的所有元素比较并可能移动它们。

2. 空间复杂度：

   • O(1)，插入排序是原地排序，除了用于交换的临时变量外，不需要额外的存储空间。

3. 稳定性：

   • 插入排序是稳定的排序算法。相等的元素在排序过程中不会改变它们的相对顺序。

4. 算法步骤：

   • 初始状态下，数组的第 1 个元素已完成排序。
   • 选取数组的第 2 个元素作为 base ，将其插入到正确位置后，数组的前 2 个元素已排序。
   • 选取第 3 个元素作为 base ，将其插入到正确位置后，数组的前 3 个元素已排序。
   • 以此类推，在最后一轮中，选取最后一个元素作为 base ，将其插入到正确位置后，所有元素均已排序。

插入排序适合于小规模数据集或者数据基本有序的情况，其效率较高。对于大规模乱序数据，插入排序的效率较低，此时通常会考虑使用更高效的排序算法，如快速排序、归并排序等。然而，插入排序的一个重要应用是在更复杂排序算法（如快速排序）中作为基础步骤，特别是在数据分割到一定小规模后，使用插入排序来完成局部排序，能有效提高整体效率。

插排实现图片如下：

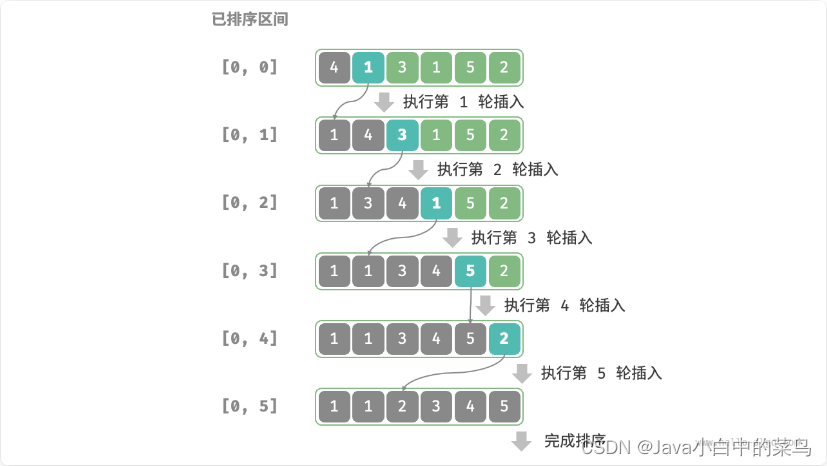
插排实现Java代码如下：

/* 插入排序 */
    void insertionSort(int[] nums) {
        // 外循环：已排序区间为 [0, i-1]
        for (int i = 1; i < nums.length; i++) {
            int base = nums[i], j = i - 1;
            // 内循环：将 base 插入到已排序区间 [0, i-1] 中的正确位置
            while (j >= 0 && nums[j] > base) {
                nums[j + 1] = nums[j]; // 将 nums[j] 向右移动一位
                j--;
            }
            nums[j + 1] = base;        // 将 base 赋值到正确位置
        }
    }
    public static void main(String[] args) {
        int[] nums = {3, 1, 5, 4, 2};
        test1 t = new test1();
        t.insertionSort(nums);
        for (int num : nums) {
            System.out.print(num + " ");
        }
    }

下图是我自己对排序代码的一些解释