【hdu 6991】Increasing Subsequence (CDQ分治)

题目链接

题目大意

给定一个 $1\sim n$ 的排列 $a_1,a_2,...,a_n$ ，求极大上升子序列（即不存在真包含它的上升子序列）的个数。（$n\le 10^5$）

思路

首先有一个 $O(n^2)$ 的做法：
记 $f_j$ 为 $a_1,a_2,...,a_i$ 中以 $a_i$ 为结尾的极大上升子序列个数。
然后 $f_j$ 对 $f_i$ 有贡献（$f_i+=f_j$）当且仅当 $a_j<a_i$ 且 $\nexists k(j<k<i),a_j<a_k<a_i$。
最后设 $a_{n+1}=n+1$ ，则 $f_{n+1}$ 即为答案。

然后发现可以利用CDQ分治进行优化。
考虑 $[l,m]$ 对 $[m+1,r]$ 中各元素的贡献，可以从小到大考虑 $[l,r]$ 中的各个数，并维护两个单调栈，$[l,m]$ 的元素下标递减，$[m+1,r]$ 的元素下标递增。
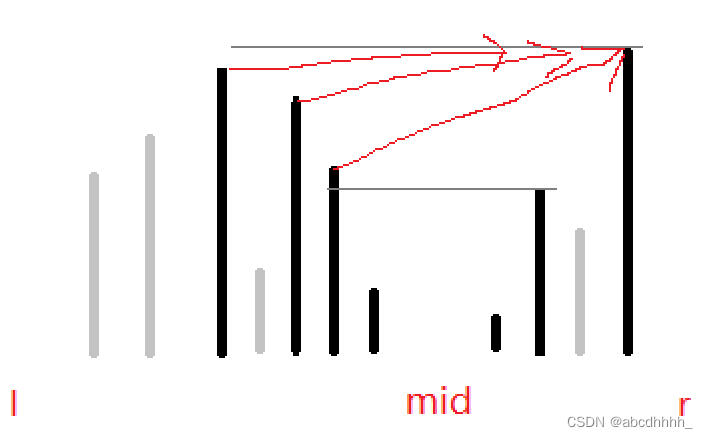
对 $i\in [m+1,r]$ ，找到 $[m+1,r]$ 栈中 $a_i$ 左侧最靠右的元素（即退栈后的栈顶） $a_j$。
然后找到 $[l,m]$ 中第一个比 $a_j$ 大的和最后一个比 $a_i$ 小的（即栈顶）元素。$[l,m]$ 栈中它们之间的元素和即 $[l,m]$ 对 $f_i$ 的贡献。

代码

#include <bits/stdc++.h>
#define rep(i, l, r) for (int i = l; i <= r; ++i)
#define per(i, r, l) for (int i = r; i >= l; --i)
using namespace std;
const int inf = 0x3fffffff;
const int N = 100005;
const int mod = 998244353;
int T;
int n;
class node {
   public:
    int id, val;
    bool operator<(const node &rhs) const { return val < rhs.val; }
} a[N];
int dp[N];
void init() {
    int mx = inf;
    rep(i, 1, n) {
        if (a[i].val < mx) {
            mx = a[i].val;
            dp[i] = 1;
        } else
            dp[i] = 0;
    }
}
void solve(int l, int r) {
    if (l == r) return;
    int mid = (l + r) / 2;
    solve(l, mid);

    sort(a + l, a + r + 1);
    static node sta1[N], sta2[N];
    static int top1, top2;
    static int s[N];
    top1 = top2 = 0;
    rep(i, l, r) {
        // printf("%d ", a[i].val);
        if (a[i].id <= mid) {
            while (top1 && sta1[top1].id < a[i].id) {
                --top1;
            }
            ++top1;
            sta1[top1] = a[i];
            s[top1] = (s[top1 - 1] + dp[a[i].id]) % mod;
        } else {
            while (top2 && sta2[top2].id > a[i].id) {
                --top2;
            }
            int j = lower_bound(sta1 + 1, sta1 + top1 + 1, sta2[top2]) - sta1;
            dp[a[i].id] = (1ll * dp[a[i].id] + s[top1] - s[j - 1] + mod) % mod;
            ++top2;
            sta2[top2] = a[i];
        }
    }
    // printf("\n");

    sort(a + l, a + r + 1, [](node x, node y) { return x.id < y.id; });

    solve(mid + 1, r);
}
int main() {
    scanf("%d", &T);
    while (T--) {
        scanf("%d", &n);
        rep(i, 1, n) {
            a[i].id = i;
            scanf("%d", &a[i].val);
        }
        ++n;
        a[n].id = a[n].val = n;
        init();
        solve(1, n);
        printf("%d\n", dp[n]);
    }

    return 0;
}