时间序列预测（二十）—— 各种滤波方法对比

在数据采集过程中，由于各种因素（如电路干扰、电源噪声、电磁干扰、采样技术的限制等）的影响，原始数据中往往会掺杂一些噪声或误差。这些噪声数据可能会严重影响最终数据的准确性，从而对后续的数据分析、模型构建或决策制定产生误导。因此，为了获得更准确、更可靠的数据，需要对原始数据进行滤波处理。

以下是我所采集的一组方向盘转角数据样本，我计划运用多种滤波技术对其进行处理，旨在通过对比分析各种滤波方法的效果，从而甄选出一种相对而言表现更为优异的滤波策略。

总的函数放在最后。

其中使用到的滤波方法有：

一、移动平均（Moving Average）

1、原理：

移动平均滤波是一种简单的平滑方法，它通过对相邻的若干个数据点进行平均来减小数据的波动。通常使用固定大小的窗口滑动计算每个数据点的平均值。

• 优点：简单，计算量小，能够有效去除低频噪声。
• 缺点：信号的动态性会丢失，延迟较大，且不适合处理高频成分。

2、Python函数：

使用 pandas 库中的 rolling().mean() 方法进行计算。

import pandas as pd

# 假设已加载数据
steering_angle = data['Steering_Angle(deg)']

# 设置窗口大小
window_size = 5

# 移动平均法
moving_average = steering_angle.rolling(window=window_size).mean()

修改一个参数：窗口大小window_size

window_size 决定了每个点的“平均范围”。window_size 较大时，平滑效果更明显，但细节会丢失；window_size 较小，平滑效果较弱，但可以较好地保留信号的波动。

• 较小的 window_size：对信号的平滑作用较小，噪声可能没有被有效去除，信号的局部波动较为明显。
• 较大的 window_size：对信号的平滑作用更强，噪声被更好地抑制，但信号的动态变化（例如快速变化或突变的部分）可能会被模糊。

3、具体平滑效果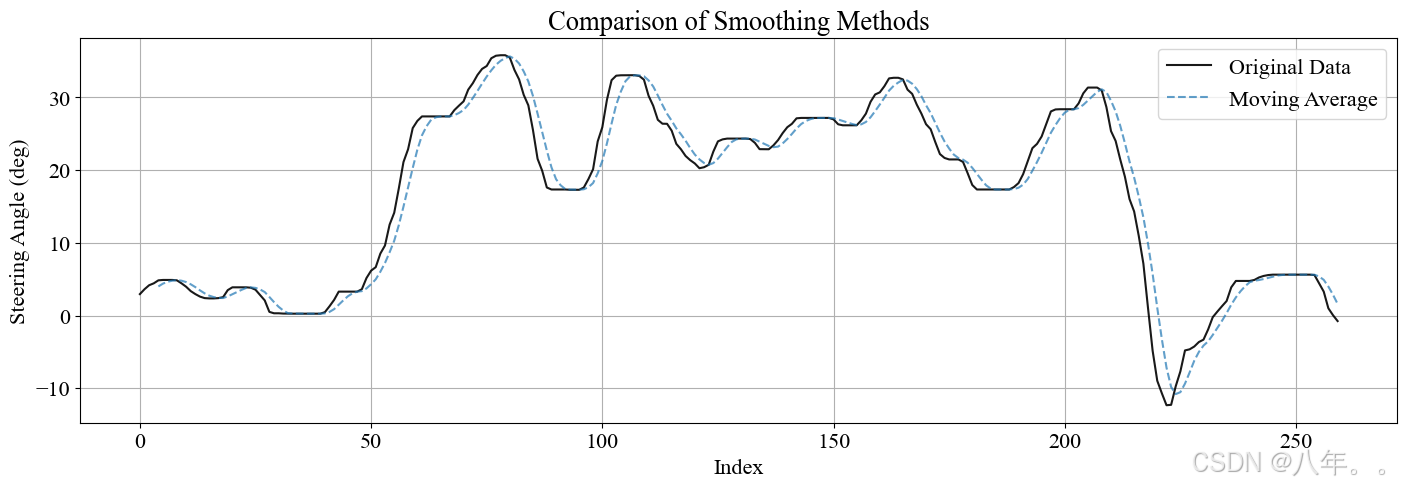

可以看到有明显延迟。

---

二、高斯滤波（Gaussian Filter）

1、原理：

高斯滤波是一种通过加权平滑信号的方法，权重由高斯函数决定。这种函数的权重分布呈钟形曲线，中心点权重大，越远离中心的点权重越小。相比其他平滑滤波方法（如简单移动平均），它更倾向于保持原始信号的形状，同时减少高频噪声。

• 优点：由于高斯函数的连续性和权重分布，高斯滤波能更平滑地抑制噪声，同时不会明显地引入阶跃现象或失真。在去噪的同时能较好地保留信号的低频部分。高斯滤波特别适合处理具有随机高频噪声的数据。
• 缺点：对于快速变化的信号可能存在模糊，尤其是频率较高的部分。

2、Python函数：

使用 scipy.ndimage 中的 gaussian_filter1d() 函数。

from scipy.ndimage import gaussian_filter1d

# 高斯滤波（标准差设置为2）
gaussian_smoothed = gaussian_filter1d(steering_angle, sigma=2)

修改一个参数：标准差sigma

sigma 是指高斯函数的标准差，控制了滤波器的平滑程度。sigma 值越大，高斯滤波器的影响范围越广，信号的平滑效果越强，但也可能会抑制更多的细节；sigma 值越小，平滑效果越弱，信号的细节保留得更多，但噪声可能没有有效去除。

3、具体平滑效果

---

三、指数平滑（Exponential Smoothing）

1、原理：

指数平滑通过给每个数据点赋予一个衰减的权重，最近的数据点权重更大，远离的数据点权重较小。其数学表达式为：

其中 α为平滑因子，X_t为当前值，S_t为平滑值。

• 优点：响应快速，适合动态变化的信号。
• 缺点：可能会抑制较高频的动态变化。

2、Python函数：

使用 pandas 中的 ewm() 函数来进行指数平滑。

# 设置平滑因子
alpha = 0.4

# 指数平滑法
exponential_smoothed = steering_angle.ewm(alpha=alpha).mean()

修改一个参数：平滑因子alpha，

alpha 控制了平滑时新数据和历史数据的相对权重，决定了对历史数据的“记忆”长度。alpha 的范围： alpha 通常在 0 到 1 之间。

• 较小的 alpha（接近 0）： 表示更多的权重给历史数据，平滑效果较强，短期波动不会对结果产生很