目录
该文章是算法设计与分析(第二版)中各章的课后习题 主编 : 李春葆
在本文中,主要是对该书第三章-分治法章节中的上机实验题以及在线编程题进行代码解答。
代码运行环境是:DEVc++
上机实验题
问题一:求解查找假币问题

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
// 采用分治法
int Find(int a[],int left,int right){
if(left == right){
return left;
}
if(left < right){
int mid = (left + right)/2;
int suml = 0,sumr = 0;
for(int i = left ; i <= mid ;i++){
suml += a[i];
}
//0 1 2 3 4 5 6
for(int i = mid + 1 ; i <= right ;i++){
sumr += a[i];
}
if(suml / (mid + 1 - left) < sumr / (right - mid)){
Find(a,left,mid);
}else{
Find(a,mid+1,right);
}
}
}
int main(){
int a[] = {1,1,1,1,1,1,0,1,1,1,1,1,1};
int len = sizeof(a)/sizeof(a[0]);
cout<<"硬币:"<<endl;
for(auto h : a){
cout<<h<<" ";
}
cout<<endl;
cout<<Find(a,0,len - 1);
return 0;
}
运行截图:

问题二:求解众数问题

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
void cut(int a[] ,int length,int &left,int &right) //将数组从中间分割成左右两块
{
int mid=length/2;
for(left=0;left<length;left++) //找到第一个等于a[mid]的值的下标
{
if(a[left]==a[mid])
{
break;
}
}
for(right=left+1;right<length;right++)//找到第一个不等于a[mid]的值的下标
{
if(a[right]!=a[mid])
{
break;
}
}
}
void fenzhi(int a[],int &num,int &max,int length){
int mid = length/2;
int left = 0,right = 0,longs = 0;
cut(a,length,left,right);
longs = right - left;
if(longs > max){
//num 是保存的众数,max是保存的众数出现的次数
max = longs;
num = a[mid];
}
if(longs == max){
if(num>a[mid]){
num = a[mid];
}
}
if(left > max){
fenzhi(a,num,max,left);
}
if(length-right > max){
fenzhi(a+right,num,max,length-right);
}
}
int main(){
int a[] = {1,2,2,2,3,5};
int n = sizeof(a)/sizeof(a[0]);
//先排序
sort(a,a+n);
int num = 0,max = 0;
fenzhi(a,num,max,n);
cout<<"众数是:"<<num<<" 重数是: "<<max<<endl;
return 0;
}
运行截图:

问题三:求解逆序对问题
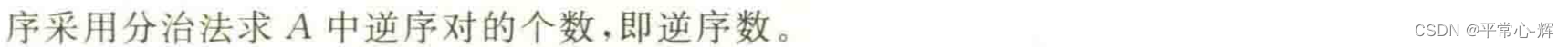
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1005;
int a[N];
int b[N]; //储存中间数组
int ans=0; //逆序数的计数
void ccount(int a[],int s,int m,int e,int b[]); //求逆序数且进行排序
void array(int a[],int s,int e,int b[]); //分治
int main()
{
int n;
cin>>n;
for(int i=0;i<n;i++){
cin>>a[i];
}
array(a,0,n-1,b);
cout<<"逆序对数位: "<<ans<<endl;
return 0;
}
void ccount(int a[],int left,int m,int right,int b[]){
int i=left,j=m+1,p= 0;
while(i<=m&&j<=right){
if(a[j]>=a[i]){
//将交换的数据保存到临时数组中
b[p++]=a[j++];
}
else if(a[j]<a[i]){
//ans计算逆序对的个数
ans+=right-j+1;
b[p++]=a[i++];
}
}
//3 1 4 5 2
while(i<=m)
b[p++]=a[i++];
while(j<=right)
b[p++]=a[j++];
//将临时数组中的数据,拷贝到原数组
for(int k=0;k<right-left+1;k++){
a[left+k]=b[k];
}
}
void array(int a[],int left,int right,int b[]){
if(left<right){
int m=left+(right-left)/2; //分治
array(a,left,m,b);
array(a,m+1,right,b);
ccount(a,left,m,right,b); //分治结果的合并
}
}运行截图:

问题四:求解半数集问题

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
int a[2008] = {};
int half(int n){
int ans = 1;
if(a[n] != 0){
return a[n];
}
for(int i = 1 ; i <= n/2 ; i++){
ans += half(i);
a[n] = ans;
}
return ans;
}
int main()
{
int n;
cin>>n;
cout<<"元素个数为: "<<half(n)<<endl;
return 0;
}
运行截图:

问题五:求解一个整数数组划分两个子数组问题

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
void quik(int a[],int left,int right,int &c){
int i = left , j = right,temp = a[left];
if(i >= j){
return;
}
while(i < j){
while(i < j && a[j] > temp ){
j--;
}
a[i] = a[j];
while(i < j && a[i] < temp){
i++;
}
a[j] = a[i];
}
a[i] = temp;
if(i == c/2){
c = i;
return;
}if(i < right/2){
quik(a,i+1,right,c);
}else{
quik(a,left,i-1,c);
}
}
int main(){
int a[] = {5,6,7,8,1,2,3,4,9,11,10};
int n = sizeof(a)/sizeof(a[0]);
int c = n-1;
quik(a,0,n-1,c);
if(c == n-1){
c = (n - 1)/2;
}
int x = 0;
for(int i = 0 ; i < n ;i++){
if(i < c){
x -= a[i];
}else{
x += a[i];
}
}
cout<<"S1 - S2 的结果为: "<<x<<endl;
return 0;
}
运行截图:

在线编程题:
问题一:求解满足条件的元素对个数问题

#include<stdio.h>
#include<algorithm>
using namespace std;
#define MAXN 200000
int a[MAXN];
int n,c;
int search(int low,int high,int x)
{
while(low<=high)
{
int mid = (low+high)/2;
if(a[mid]==x)
{
int count=1,i;
i=mid-1;
while(i>=low&&a[i]==x)
{
count++;
i--;
}
i=mid+1;
while(i<=high&&a[i]==x)
{
count++;
i++;
}
return count;
}
else if(x>a[mid])
low=mid+1;
else
high=mid-1;
}
return 0;
}
int main()
{
scanf("%d%d",&n,&c);
for(int i=0;i<n;i++)
scanf("%d",&a[i]);
sort(a,a+n);
int ans = 0;
for(int j=0;j<n-1;j++)
ans+=search(j+1,n-1,a[j]+c);
printf("A[i]-A[j]=c出现的次数为%d\n",ans);
return 0;
}运行截图:

问题二:求解查找最后一个小于等于指定数的元素问题

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
//输入样例:5 3 1 2 3 4 6 5 1 3
//输出样例:4 1 3
//二分查找
int quik(int a[],int left,int right,int target){
if(a[left] > target){
return -1;
}
if(left == right && a[left] <= target) {
return a[left];
}
while(left <= right){
int mid = (left + right)/2;
if(a[mid] <= target && a[mid+1]>target){
return a[mid];
}else if(a[mid] < target && a[mid+1]<=target) {
left = mid+1;
} else if(a[mid] > target){
right = mid-1;
}
}
}
int main(){
int n ,x;
cin>>n>>x;
int a[n] , b[x];
int i;
for(i = 0 ; i < n;i++){
cin>>a[i];
}
cout<<"结果为: "<<endl;
for(i = 0 ; i < x;i++){
cin>>b[i];
//二分查找算法入口
cout<<quik(a,0,n-1,b[i])<<endl;
}
return 0;
}
运行截图:

问题三:求解递增序列中与X最接近的元素问题

#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
using namespace std;
//输入
//3 2 5 8
//2 10 5
//输出: 8 5
//二分查找
int quik(int a[],int left,int right,int target){
//判断边界条件
if(target <= a[left]){
return a[left];
}else if(target >= a[right]){
return a[right];
}
while(left <= right){
int mid = (left + right)/2;
if(a[mid] <= target && a[mid+1] > target){
if(abs(target - a[mid]) < abs(target - a[mid+1])){
return a[mid];
}else{
a[mid+1];
}
}else if(a[mid] < target && a[mid+1]<=target) {
left = mid+1;
} else if(a[mid] > target){
right = mid-1;
}
}
}
int main(){
int n ,x;
cin>>n;
int a[n] , b[x];
int i;
for(i = 0 ; i < n;i++){
cin>>a[i];
}
cin>>x;
cout<<"结果为: "<<endl;
for(i = 0 ; i < x;i++){
cin>>b[i];
//二分查找算法入口
cout<<quik(a,0,n-1,b[i])<<endl;
}
return 0;
}
运行截图:
问题四:求解安“最多排序”到“最少排序”的顺序排列问题


#include<bits/stdc++.h>
using namespace std;
#define MAXN 15
#define MAXM 105
//10 6
//AACATGAAGG
//TTTTGGCCAA
//TTTGGCCAAA
//GATCAGATTT
//CCCGGGGGGA
//ATCGATGCAT
int ans;
void Merge(char a[],int low,int mid,int high){
int i=low;
int j=mid+1;
int k=0;
char *tmp=(char *)malloc((high-low+1)*sizeof(int));
while(i<=mid&&j<=high){
if(a[i]>a[j]){
tmp[k++]=a[j++];
ans+=mid-i+1;
}else tmp[k++]=a[i++];
}
while(i<=mid ) tmp[k++]=a[i++];
while(j<=high) tmp[k++]=a[j++];
for(int k1=0;k1<k;k1++){
a[low+k1]=tmp[k1];
}
free(tmp);
}
void MergeSort(char a[],int low,int high){
if(low<high){
int mid=(low+high)/2;
MergeSort(a,low,mid);
MergeSort(a,mid+1,high);
Merge(a,low,mid,high);
}
}
int Inversion(char a[],int n){
ans=0;
MergeSort(a,0,n-1);
return ans;
}
typedef struct {
int v;
int i;
}ElemType;
struct Cmp{
bool operator()(const ElemType &s,const ElemType &t) const{
return s.v<t.v;
}
};
int main(){
int i,n,m;
char str[MAXM][MAXN];
ElemType b[MAXM];
memset(b,0,sizeof(b));
char tmp[MAXN];
cin>>n>>m;
for(int i=0;i<m;i++) {
cin>>str[i];
}
for(int i=0;i<m;i++){
strcpy(tmp,str[i]);
b[i].v=Inversion(tmp,n);
b[i].i=i;
}
stable_sort(b,b+m,Cmp());
cout<<"结果为: "<<endl;
for(int i=0;i<m;i++){
cout<<str[b[i].i]<<endl;
}
}
运行截图:









 本文介绍了《算法设计与分析》一书中关于分治法的上机实验题和在线编程题,包括查找假币、求解众数、计算逆序对等问题的解决方案。所有代码均使用C++编写,并在DEVc++环境下运行。通过分治策略,这些算法有效地解决了各自的问题。
本文介绍了《算法设计与分析》一书中关于分治法的上机实验题和在线编程题,包括查找假币、求解众数、计算逆序对等问题的解决方案。所有代码均使用C++编写,并在DEVc++环境下运行。通过分治策略,这些算法有效地解决了各自的问题。
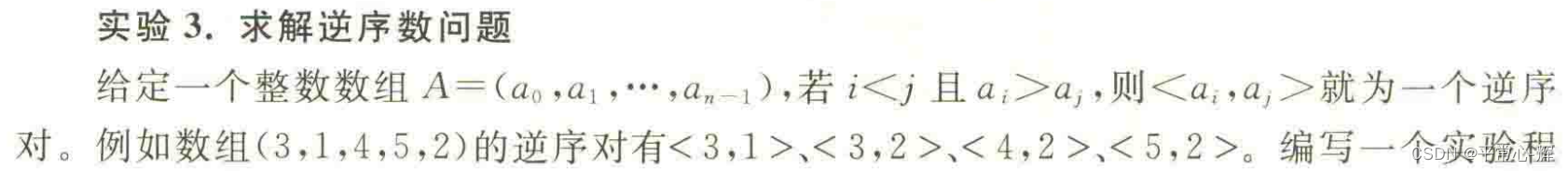


















 2742
2742

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








