C语言实现(不同阶数的)矩阵求逆（已用350个2-8阶的矩阵测试）

1、生成测试文件的代码

测试文件：

fp = fopen("Array_Test_Document.txt","r");

文件名为Array_Test_Document.txt  ，如果想要更换自己测试数据，仅需要在同一个目录下生成一个名为Array_Test_Document.txt 的文件，在文件中写入矩阵数据，每行为一个矩阵，每个元素之间用空格隔开。

#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#include<math.h>

//该代码是创建了一个文件，文件的内容是2-8阶的可逆矩阵，每个阶数的矩阵各50个。
//文件的每一行都是一个矩阵，每个矩阵的元素之间用空格分开。


void Write_to_file(FILE *fp);
float HlsCalculate(float **x,const int row,const int column);
int main(){
	FILE *fp;
	int i,j,k;

	//设置随机数
	srand((unsigned)time(NULL));
	
	fp = fopen("Array_Test_Document.txt","w");
	if (fp != NULL){
		Write_to_file(fp);
    	}else{
		printf("文件打开失败：\n");
	}

    fclose(fp);
    return 0;
}



//求行列式
float HlsCalculate(float **x,const int row,const int column){
	float hls = 0;
	float **c;
	int i,j,k;


	//动态分配二维数组
	c = (float **)malloc(sizeof(float *) * row);
	//分配列数
	for(j = 0;j < row;j++){
		c[j] = (float *)malloc(sizeof(float) * column);
	}

	//1阶2阶行列式计算
	if(row == 1){
		return x[0][0];
	}
	if(row == 2){
		float z = x[0][0]*x[1][1] - x[0][1]*x[1][0];
		//printf("2dimention hls= %f\n",k);
		return z;
	}



	//3阶以上求行列式
	for(j = 0;j < row ;j++){
		for(i = 0 ; i < column - 1;i++){
			for(k = 0 ; k < row - 1;k++){
				if(k<j)c[i][k] = (float)x[i+1][k];
				if(k>=j)c[i][k] = (float)x[i+1][k+1];
			}
		}
		hls += pow(-1,j)*x[0][j]*HlsCalculate(c,row-1,column-1);
	}
	//printf("原矩阵的行列式 = %f\n",hls);
	return hls;
}


//将行列式不为0的矩阵写入文件
void Write_to_file(FILE *fp){


	int i,j,k;
	i = 0;
	
	//矩阵的阶数
	int matrix_size;

	//接受随机数值的临时变量
	int  a;

	//count 用于记录每个维度的矩阵写入文件的个数
	int count;
	count = 0;


	do{
		//int matrix_size;
		//设置生成矩阵的维度
		matrix_size = 2;
		matrix_size += count / 50;
		
		 if(matrix_size == 9){
			break;
		}
		

		//动态分配一个二维数组
		float **p1;
		//分配行数
	        p1 = (float **)malloc(sizeof(float *) * matrix_size);
		//分配列数
		for(j = 0;j < matrix_size;j++){
			p1[j] = (float *)malloc(sizeof(float) * matrix_size);
		}
			
		//给数组中放入随机值
		for(j = 0;j < matrix_size;j++){
			for(k = 0;k < matrix_size;k++){
				//rand()%10 是设置数组中元素的值为0-10之间
				a = rand()%10;
				p1[j][k] = a;
			}
		}


		//求矩阵的行列式，如果行列式的绝对值在1 - pow(10,matrix_size)之间则将该数据写入文件
		//determinant 用于接受矩阵的行列式值
		float determinant;
		determinant = HlsCalculate(p1,matrix_size,matrix_size);
		if((determinant >= -pow(10,matrix_size) && determinant <= -1) ||
			(determinant <= pow(10,matrix_size) && determinant >= 1)){
			count ++;
			for(j = 0;j < matrix_size;j++){
				for(k = 0 ; k < matrix_size;k++){
					fprintf(fp,"%.2f",p1[j][k]);
					fprintf(fp," ");
				}
			}
			fputc('\n',fp);
		}
		free(p1);

	// matrix_size < 9 是指写入的可逆矩阵维度在2-8之间
	}while(matrix_size  < 9);  
    	
	


}

2、部分测试文件截图

3、C代码实现矩阵求逆，用生成的测试文件测试代码

#include<stdio.h>
#include<math.h>
#include<stdlib.h>

void inverseArr(float **inverse,float **result,int N);
float HlsCalculate(float **x,const int row,const int column);

void mulMatrix(float **a,float **b,const int row);

int main(){

        
	int i,j,k,count;	

	//打开文件
	FILE *fp;
	fp = fopen("Array_Test_Document.txt","r");
	if(fp == NULL){
		printf("文件打开失败：");
		return -1;
	}

	count =0;
	while(++count <= 350){
	
		int row = 2 + (count-1)/50;
		int column = 2 + (count-1)/50;
		int i,j,k;


		//(0000000)动态分配一个二维数组,增广矩阵
		float **inverse;
        	//分配行
		inverse = (float **)malloc(sizeof(float *) * row); 
		//分配列数                 
		for(j = 0;j < row;j++){
	        	inverse[j] = (float *)malloc(sizeof(float)
			       	* column * 2);
		}
		

		//(1111111)动态分配一个二维数组,用于保存计算得到的逆矩阵
		float **ni_matrix;
        	//分配行
		ni_matrix = (float **)malloc(sizeof(float *) * row); 
		//分配列数                 
		for(j = 0;j < row;j++){ 
        		ni_matrix[j] = (float *)malloc(sizeof(float)* column );
		}


		//(2222222)动态分配一个二维数组,用于保存测试文件中的矩阵元素
		float **a;
        	//分配行
		a = (float **)malloc(sizeof(float *) * row); 
		//分配列数                 
		for(j = 0;j < row;j++){ 
        		a[j] = (float *)malloc(sizeof(float)* column );
		}


		//读取文件中的数据
		for(i = 0 ; i < row;i++){
			for(j = 0;j < column; j++){
				fscanf(fp,"%f",&a[i][j]);
			}
		}



		//打印原矩阵
		printf("第 %d 个矩阵\n",count);
		printf("==========原矩阵==========\n");
		for( i = 0; i < row ;i++){
			for(j = 0 ; j < column ; j++){
				printf("%6.2f ",a[i][j]);
			}
			printf("\n");
		}



		//求原矩阵的行列式,判断是否可逆
		//if行列式==0 则不可逆
		float  hls;
		hls = HlsCalculate(a,row,column);
		//printf("&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&7&&&&行列式 = %.2f\n",hls);
		if(hls == 0){
			printf("该方阵的行列式==0，不可逆\n");
			continue;
		}


		//初始化增广矩阵
		//float inverse[N][2*N] = {0};
		for(i = 0 ; i < row;i++){
			for(j = 0 ; j < 2 * column;j++){
				if(i < row && j < row){
					inverse[i][j] = a[i][j];
				}else if(i + row== j){
					inverse[i][j] = 1.00;
				}else {
				
					inverse[i][j] = 0.00;
				}
			}
		}
	


		//求逆矩阵，并打印
		inverseArr(inverse,ni_matrix,row);

		//打印
		printf("==========逆矩阵==========\n");
		for( i = 0; i < row ;i++){
			for(j = 0 ; j < row ; j++){
				printf("%6.2f ",ni_matrix[i][j]);
			}
			printf("\n");
		}

		//原矩阵与逆矩阵的乘法运算,并输出结果矩阵
		mulMatrix(a,ni_matrix,row);

		free(a);
		free(inverse);
		free(ni_matrix);

		}
	
}


//矩阵乘法

void mulMatrix(float **a,float **b,const int row){
	int k ,i,j,p;
	k = row;
	int len = 0;

	//value1 用于保存矩阵的某一行和一列元素的相乘积的和
	float value1 = 0;

	//动态分配一个二维数组,用于保存矩阵乘法的结果
	float **c;
        //分配行
	c = (float **)malloc(sizeof(float *) * row); 
	//分配列数                 
	for(j = 0;j < row;j++){ 
        	c[j] = (float *)malloc(sizeof(float)* row );
		}
/*
	for(i = 0 ; i < k ;i++){
	
		for(j = 0 ;j < k ;j++){
		
			c[i][j] = 0;
		}
	}

	*/
	for( i = 0; i < k;i++){
		for( j = 0;j < k ;j++){
			for( p = 0 ; p < k;p++){
			value1 += a[i][p] * b[p][j];
			}
			c[i][len++] = value1;
			value1 = 0;
			if(len == k){
				len =0;
			} 
		}	
	}	

	//打印矩阵乘法的结果
	printf("====================原矩阵与逆矩阵的乘积================\n");
	for(int i = 0; i < k;i++){
		for(int j = 0;j < k ;j++){
			printf("%6.2f ",c[i][j]);
		} 
		printf("\n");
		
	}

	free(c);
}




//求行列式
float HlsCalculate(float **x,const int row,const int column){
	float hls = 0;

	int i ,j , k ;
	//动态分配一个二维数组
	float **c;
	c = (float **)malloc(sizeof(float *) * row); 
	for(j = 0;j < row;j++){
        	c[j] = (float *)malloc(sizeof(float)
			       	* column);
	}

	if(row == 1){
		return x[0][0];
	}
	if(row == 2){
		float k = x[0][0]*x[1][1] - x[0][1]*x[1][0];
		//printf("2dimention hls= %f\n",k);
		return k;
	}
	//求行列式
	for(j = 0;j < row ;j++){
		for(i = 0 ; i < column - 1;i++){
			for(k = 0 ; k < row - 1;k++){
				if(k<j)c[i][k] = x[i+1][k];
				if(k>=j)c[i][k] = x[i+1][k+1];
			}
		}
		hls += pow(-1,j)*x[0][j]*HlsCalculate(c,row-1,column-1);
	}
	//printf("原矩阵的行列式 = %f\n",hls);
	free(c);
	return hls;
}




//求逆
void inverseArr(float **inverse,float **result,int N){
	int i , j ,k;
	//float temp[2*N] ={0};
	for(i = 0 ;i < N ;i++){
		if(inverse[i][i] == 0){
			for(j = i + 1 ;j < N ;j++){
				if(inverse[j][i] != 0){
					break;
				}
			}
			for(k = 0; k < 2*N;k++){
				inverse[i][k] += inverse[j][k]; 
			}
		}
		float tmp = inverse[i][i];
		//
	       if(inverse[i][i] != 1){
	       		for(k = 0;k<2*N;k++){inverse[i][k] /= tmp;}
	       }
		//化为上三角矩阵
	       for(j=i+1;j<N;j++)
		{
			float tem_2 = inverse[j][i];
			for(k=i;k<2*N;k++)
			{
				inverse[j][k] = inverse[j][k] - tem_2 *
				       	inverse[i][k];
			}
		}
	}



	//将前部分矩阵化为E
	for(i = N-1 ; i >=0 ; i--){
		for(j = N - 1;j>i;j--){	
			if(inverse[i][j] == 0){continue;}
			float tmp = inverse[i][j];
			for(k = j;k< 2*N;k++){inverse[i][k] -= inverse[j][k]*tmp;}
		
		}
	}
	//保存在结果数组中
	for( i = 0; i < N ;i++){
		for(j = 0 ; j < N ; j++){
			result[i][j] = inverse[i][j+N];
		}
	}


} 

4、代码环境Linux

5、部分实验结果截图

 

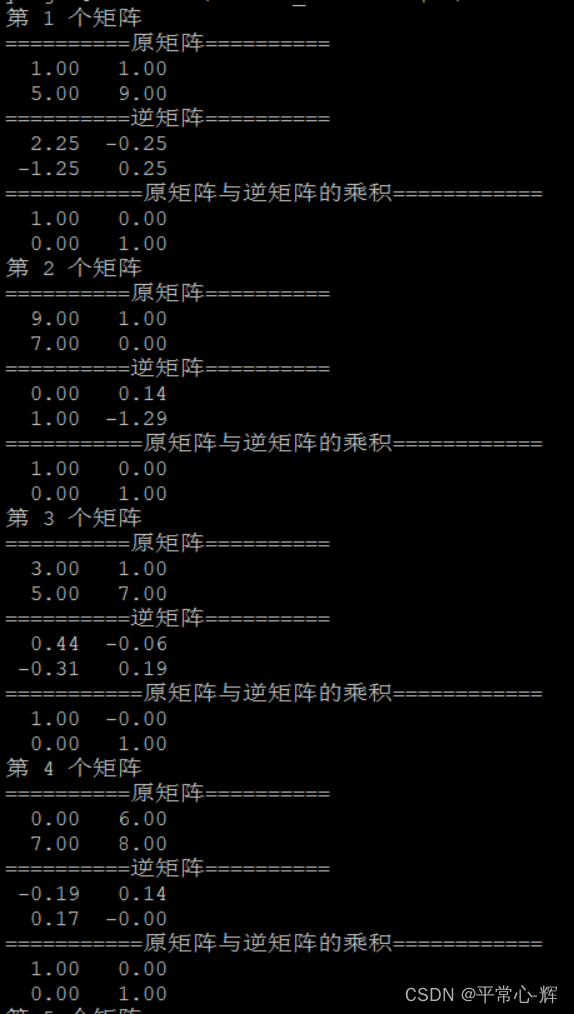
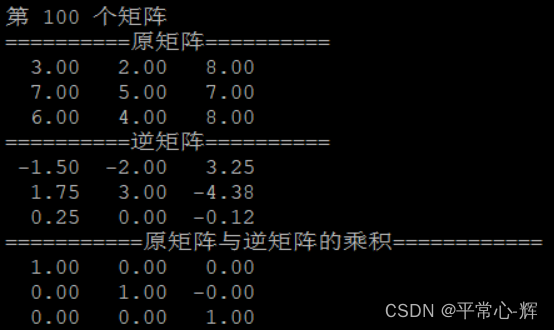
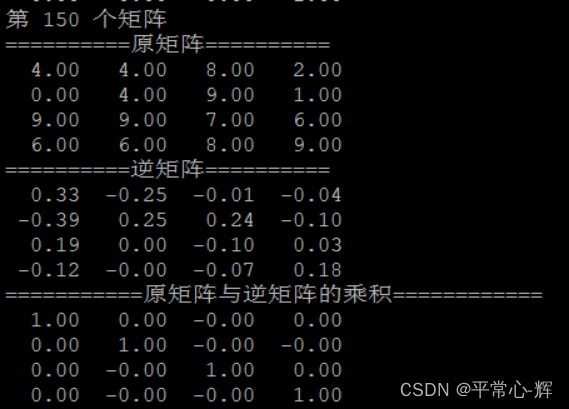
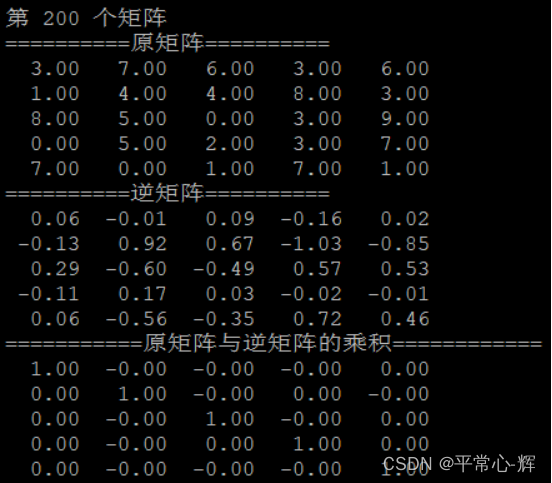
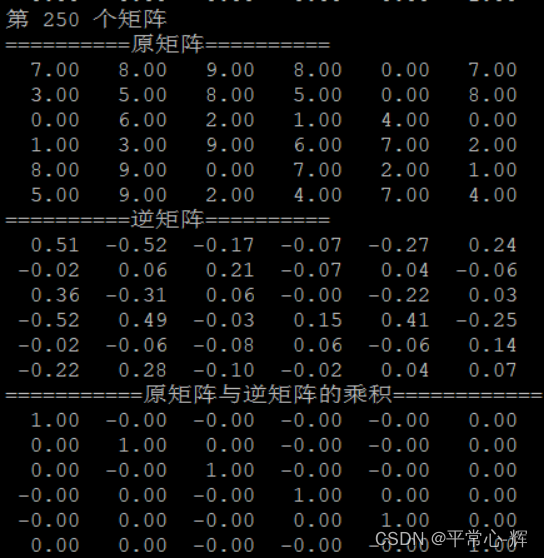
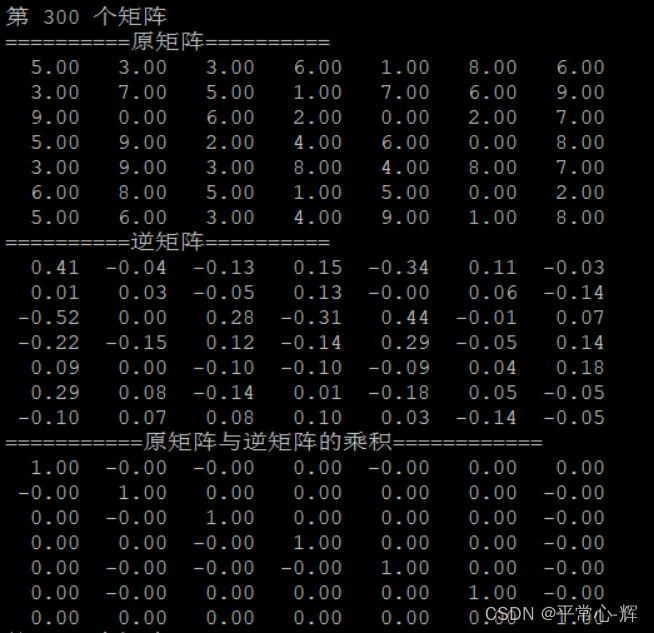
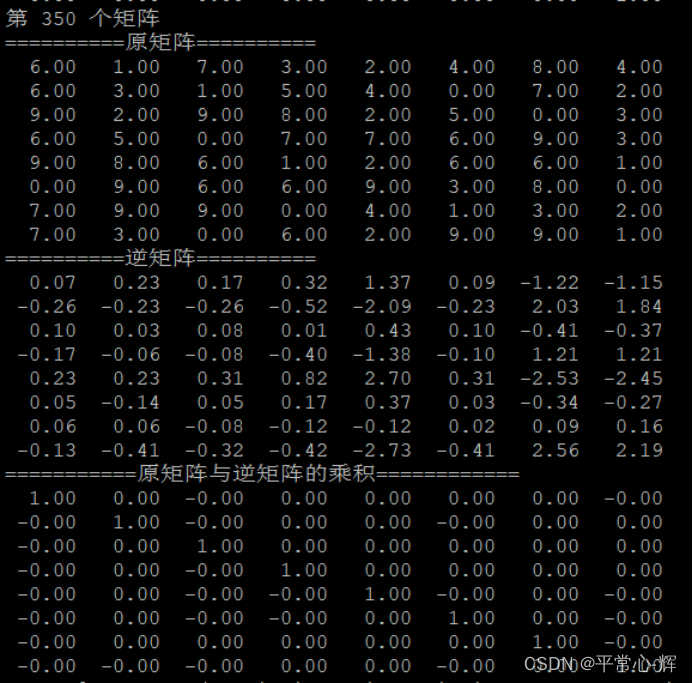
 gitee路径：

C语言: 0-1，C语言学习路程 - Gitee.com