【Leetcode动态规划--回文】647.回文子串的数量(连续) 5.最长回文子串(连续) 516.最长回文子序列(不连续)

总结

这两个题和之前的公共子序列一样，都分连续不连续，

连续的->dp定义为结尾->状态来源只有一个->结果是过程中求最大或过程中记录

不连续->dp定义为范围->状态来源有两个->结果永远是dp[0][len]等这种dp数组的最终值

Leetcode647

1.问题描述

2.解决方案

a.dp的定义就是回文的定义dp[i][j]:[i,j]闭区间是否为回文子串

b.递推吧也不用多说，按照定义来就好

c.遍历顺序要以递推逻辑来定，由下图可见

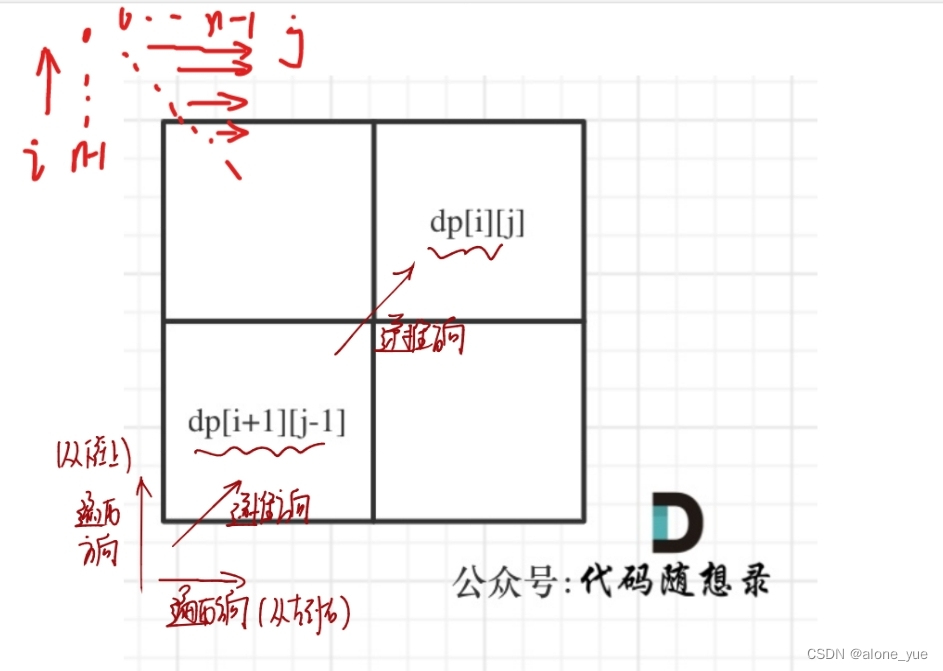
d.由定义j>=i，所以遍历只遍一半就好，j从i开始

for(int i=len-1;i>=0;i--){
   
	for(int j=i;j<=len-1;j++){
   

class Solution {
   
public:
    int countSubstrings(string s) {
   
        //1.
        int len=s.size();

        //2.
        vector<vector<bool> > dp(len,vector<bool>(len,false));

        //3.
        int ans=0;
        for(int i=len-1;i>=0;i--){
   
            for(int j=i;j<=len-1;j++){
   
                if(s[i]==s[j]){
   
                    if(j-i<=1) {
   dp[i][j]=true; ans++;}
                    if(j-i>1&&dp[i+1][j-1]==true) {
   dp[i][j]=true; ans++;}
                }
            }
        }

        //4.
        return ans;