这是一个C++课后习题,具体要求如下:
要求:输入两个字符串,输出它们的最长公共子串,包括长度。设计一个类String,包括一个len(字符串长度)和字符串指针s。即:
下面展示一些题目给的已知代码:
class String{public:
String( );
void getstring( );
void display( );
friend String maxsubstring(String str1, String str2);
private:
int len;
char *s;
};
//成员函数如下:
void getstring( )//从用户获取一个字符串
void displa( )//输出字符串
friend String maxsubstring(String str1,String str2//友元函数,求两个字符串的最长公共子串解题思路:
//方案1:找出所有的公共子串vector,确定公共子串的的最大长度,从已知的子串中选择性输出
/*方案2:动态规划,即
(1)对于这两个字符串,先标记相同字符的在矩阵中为1否则为0:
(2)那么公共子串即为对角线为1的,只需在其中找到最长的1的对角线即可,
这里我们可以把对角线(i, j)表示为1+(i-1, j-1),来达到记录当前公共子串长度的目的.
X A B C D E→X A B C D E(str1)
A 1 0 0 0 0 → A 1 0 0 0 0
D 0 0 0 1 0 →D 0 0 0 1 0 maxlength=2
E 0 0 0 0 1 →E 0 0 0 0 2
(str2)
采用动态规划解题↓
以下是实现代码:
#include<iostream>
#include<vector>
using namespace std;
class String
{public:
String(){s=NULL;}
void getstring( );//从用户获取一个字符串
void display(char[]);//输出字符串
friend void maxsubstring(String str1, String str2,vector<String>&s);//友元函数,求两个字符串的最长公共子串
private:
int len;
char *s;
};
void String::getstring()
{
s=new char[];
cout<<"输入字符串:"<<endl;
gets(s);//函数gets在字符数组后增添了'\0'
for(len=0;s[len]!='\0';len++);
}
void String::display(char *name)
{
if(s==NULL)cout<<"error!";
else
cout<<name<<"字符串="<<s<<".(长度为"<<len<<")"<<endl;
}
void maxsubstring(String str1, String str2,vector<String>&s)
{
int i,j;
String temp;
//方便后续表示字符所创建的指针
char *s1=str1.s;
char *s2=str2.s;
//用单个数组表示一列的数值,如上例中的第一列1 0 0;因此,由于单一数组的缘故,需要从后向前修改,避免前值被修改
int *counter=new int[str2.len];
//初始化为0
for(i=0;i<str2.len;i++)counter[i]=0;
//记录最大子串的长度和在str2中的末位置
int maxlen=0;
vector<int>pos;
//按从第一列到最后一列(str1),从下往上(str2)的顺序
for(i=0;i<str1.len;i++)
{
//使str2.c指向str2字符串的末字符
for(j=str2.len-1;j>=0;j--)
{
if(*&s2[j]==*&s1[i])
{
if(0==j)
{
counter[j]++;
}
else counter[j]=counter[j-1]+1;
if(counter[j]>maxlen)
{
pos.clear();
maxlen=counter[j];
pos.push_back(j);
}
//可能出现存在多个最长子串
else if(counter[j]==maxlen)
{
pos.push_back(j);
}
}
else counter[j]=0;
}
}
//不存在最长公共子串的情况
if(0==maxlen)
{
delete []counter;
cout<<"No Found!"<<endl;
return;
}
//提取待求最长子串,多个pos表示有多个最长子串
for(i=0;i<pos.size();i++)
{
char *substr=new char[maxlen+1];
for(j=0;j<maxlen;j++)
{
//pos-maxlen+1表示最长子串第一个1的位置
substr[j]=*&s2[pos[i]-maxlen+1+j];
}
substr[j]='\0';
temp.s=substr;
temp.len=maxlen;
s.push_back(temp);
}
delete []counter;
return;
}
int main()
{
String s1,s2;
vector<String>max;
s1.getstring();
s2.getstring();
s1.display("s1");
s2.display("s2");
maxsubstring(s1,s2,max);
for(vector<String>::iterator it=max.begin();it!=max.end();it++)
it->display("s1和s2最长公共子字符串");
return 0;
}值得一提的是,为了实现一些要求,我对友元函数的定义稍稍改动了一下。
原定义:
friend String maxsubstring(String str1, String str2);改为:
friend void maxsubstring(String str1, String str2,vector<String>&s);输出结果:
未找到最长公共子串
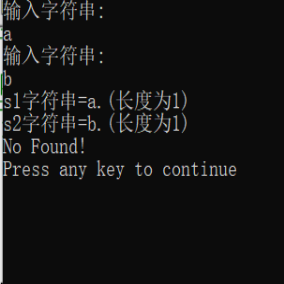
有一个最长公共子串
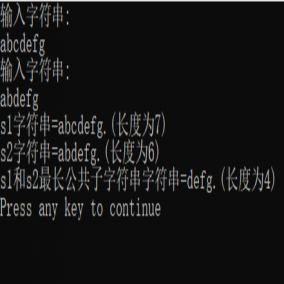
有多个最长公共子串
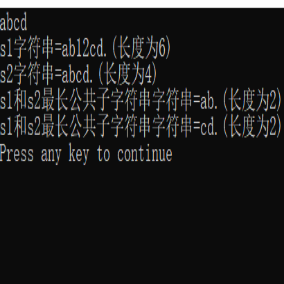























 368
368










