Leetcode 169 多数元素

最新推荐文章于 2023-11-22 15:55:48 发布

右眸Remnant

最新推荐文章于 2023-11-22 15:55:48 发布

阅读量88

点赞数

CC 4.0 BY-SA版权

分类专栏：算法文章标签： leetcode 算法职场和发展

本文链接：https://blog.youkuaiyun.com/qq_45888932/article/details/123314004

算法专栏收录该内容

16 篇文章

订阅专栏

本文介绍了如何使用HashMap统计和遍历解决LeetCode中的Majority Element问题，同时对比了两种方法：HashMap计数和摩尔投票法，它们的时间复杂度均为O(n)，但空间复杂度分别为O(n)和O(1)。摩尔投票法则解释了为何这种方法在寻找多数元素时高效有效。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

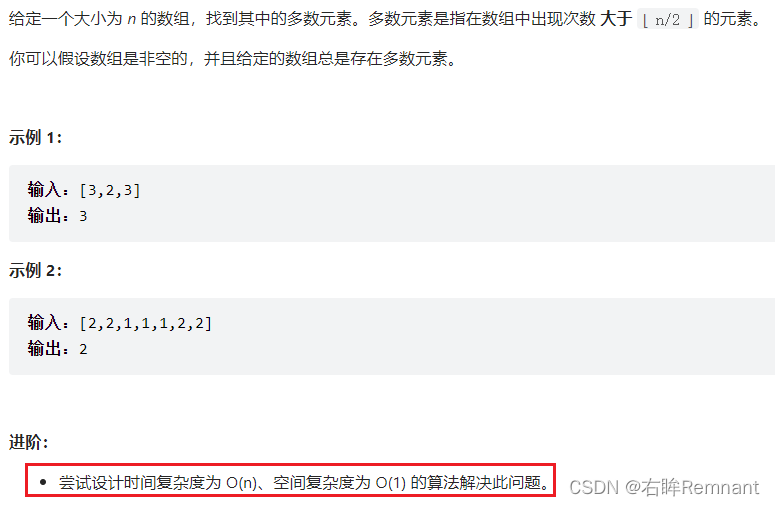
链接： https://leetcode-cn.com/problems/majority-element/

基础版：

HashMap统计次数，然后遍历；时间复杂度O(n), 空间复杂度O(n)

代码：

class Solution {
    public int majorityElement(int[] nums) {
         Map<Integer, Integer> map = new HashMap<>();
        int len = nums.length;
        for (int i = 0; i < len; i++) {
            if (map.containsKey(nums[i])) {
                map.put(nums[i], map.get(nums[i]) + 1);
            } else {
                map.put(nums[i], 1);
            }
        }
        int res = -1;
        for (Map.Entry<Integer, Integer> key : map.entrySet()) {
            if (key.getValue() > len / 2) res = key.getKey();
        }
        return res;
    }
}

摩尔投票法：

候选人(cand_num)初始化为nums[0]，票数count初始化为1。
当遇到与cand_num相同的数，则票数count = count + 1，否则票数count = count - 1。
当票数count为0时，更换候选人，并将票数count重置为1。
遍历完数组后，cand_num即为最终答案。

为何这行得通呢？
投票法是遇到相同的则票数 + 1，遇到不同的则票数 - 1。
且“多数元素”的个数> ⌊ n/2 ⌋，其余元素的个数总和<= ⌊ n/2 ⌋。
因此“多数元素”的个数 - 其余元素的个数总和的结果肯定 >= 1。
这就相当于每个“多数元素”和其他元素两两相互抵消，抵消到最后肯定还剩余至少1个“多数元素”。

时间复杂度O(n), 空间复杂度O(1)

代码：

class Solution {
    public int majorityElement(int[] nums) {
        int len = nums.length;
        int res = nums[0];
        int count = 1;
        for (int i = 1; i < len; i++) {
            if (count == 0) res = nums[i];
            if (nums[i] != res) count --;
            else count ++;
        }
        return res;
    }
}