单调栈,顾名思义:具有单调性的栈。
单调递增栈(出栈为单调递增),则栈内元素为单调递减
单调递减栈(出栈为单调递减),则栈内元素为单调递增
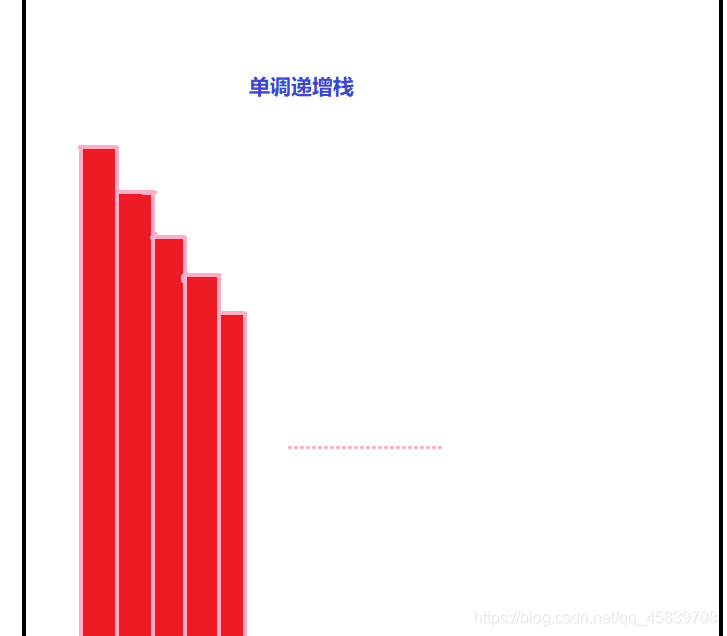
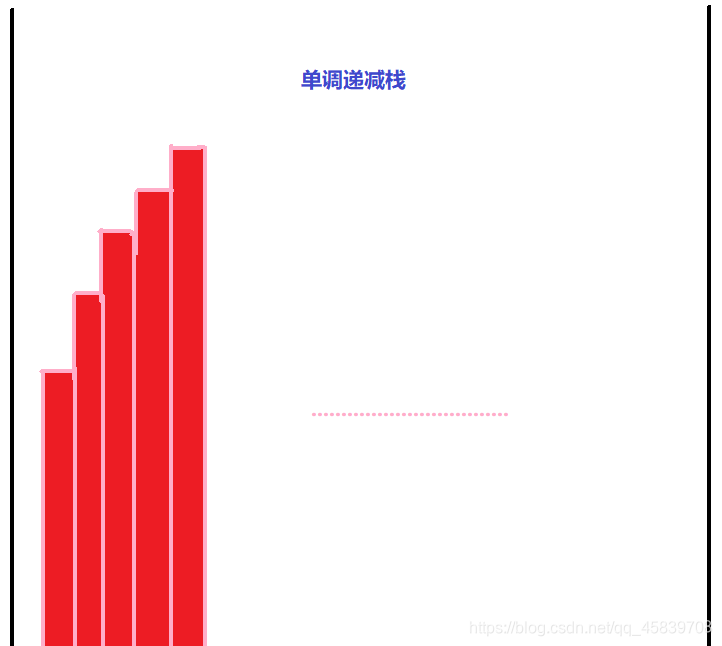
因为 栈 为 前进后出
单调栈代码(此处为递减)
stack<int>st;
for(int i = 0; i < v.size(); i++)
{
if(st.empty() || v[i] > st.top())
{
st.push(v[i]);
}
else
{
while(!st.empty() && v[i] <= st.top())
{
st.pop();
}
st.push(v[i]);
}
}
一个具体例题来讲讲单调栈应用
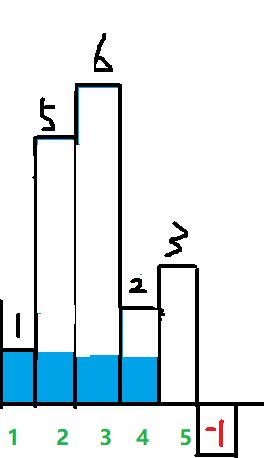
柱状图中的最大矩形
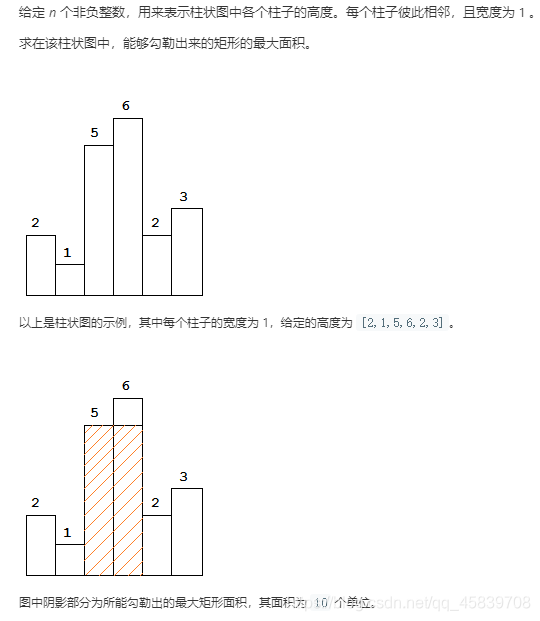

做这个题我们需要找到 每一块 的 左右边界,何为左右边界?
我用图来说明:
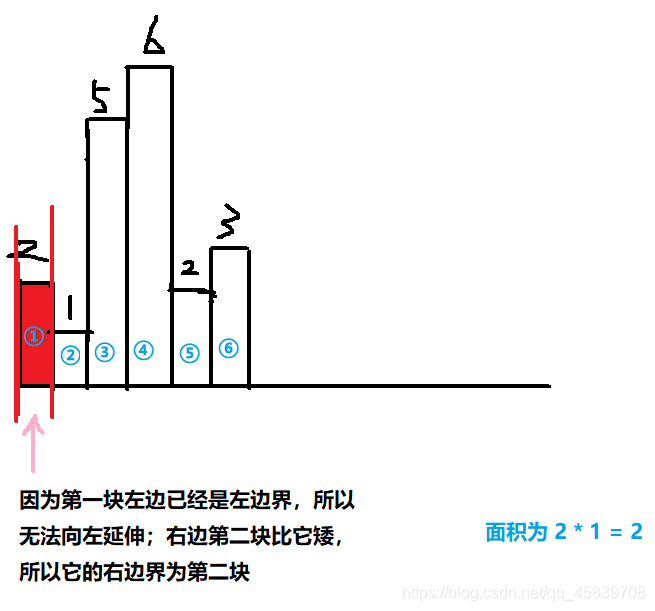
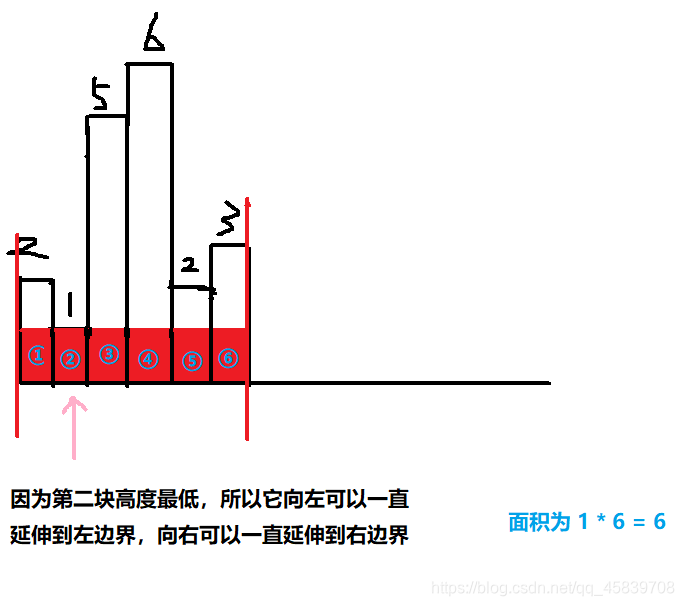
只有高度大于或等于 当前这个矩形 才能够延伸
上面两张图分别是求第一、二块可以达到的面积。
左边界指从当前的这个 矩形 i 向左 直到 遇见第一个高度比它低的矩形或者到达最左边
右边界同理
运用单调栈代码如下:
int Lagest_S(vector<int>& height)
{
height.push_back(-1);
stack<int>st;
int top, s, max_S = 0;
for(int i = 0; i < height.size(); i++)
{
if(st.empty() || height[i] >= height[st.top()])
{
st.push(i);
}
else
{
while(!st.empty() && height[i] < height[st.top()])
{
top = st.top();
st.pop();// 弹出,因为必须保证单调性
s = (i - top) * height[top];
if(s > max_S)
max_S = s;
}
st.push(top);
height[top] = height[i];
// 此处为重点之处!!!
}
}
return max_S;
}
例如{1,5,6,2,3}我们一步一步来
右边红方框表示栈;括号外面数字表示下标;括号里面数字表示高
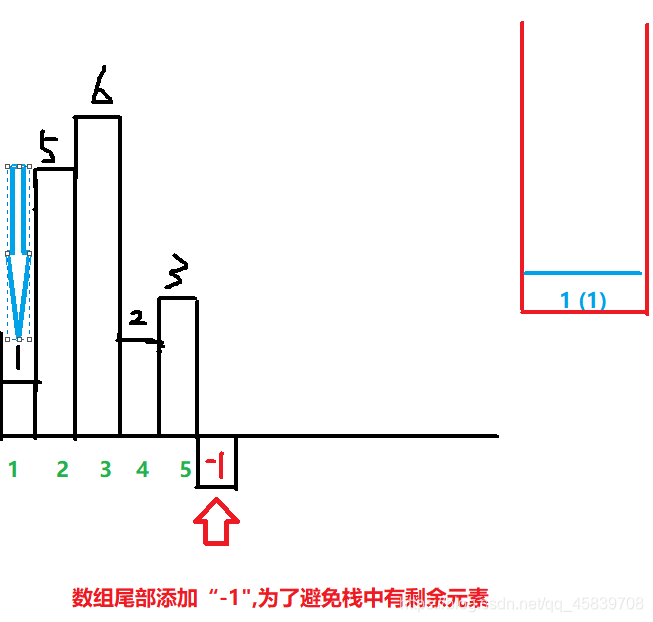
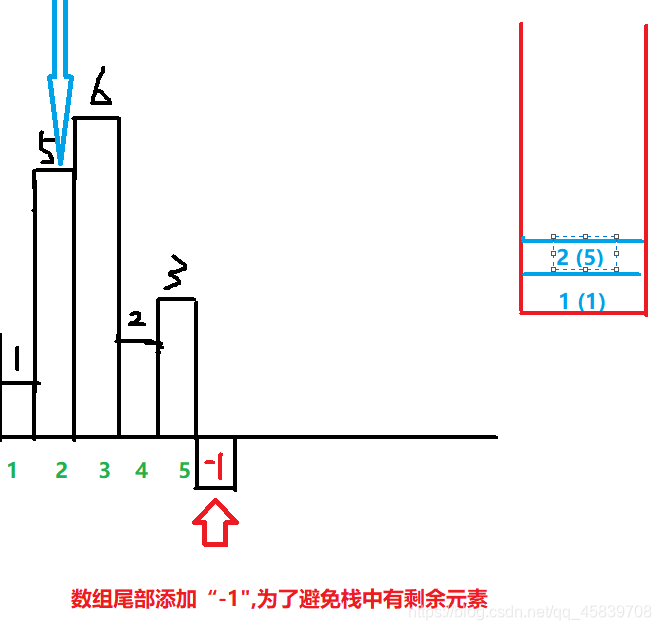
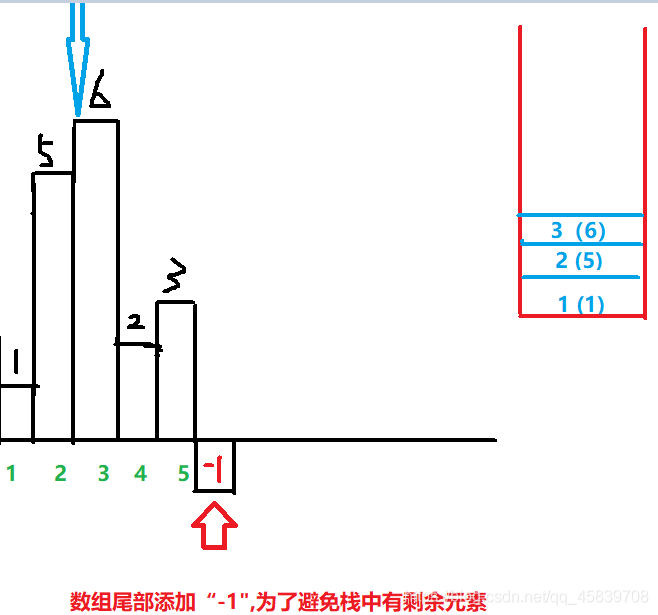
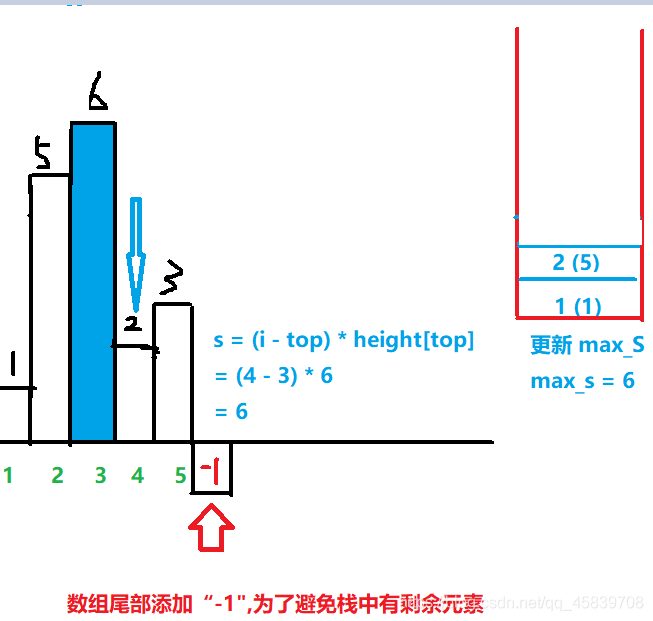
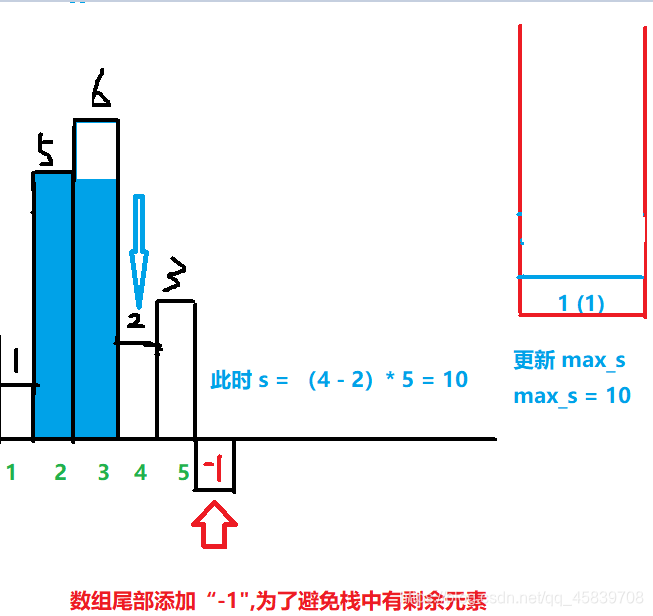
接下来到了这一步了:
st.push(top);
height[top] = height[i];
这一步执行后使得 栈 中变成这样
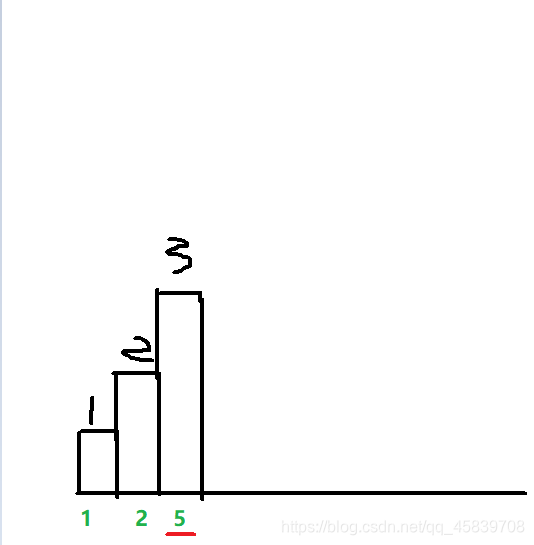
这样才能实现对下面两块面积的计算
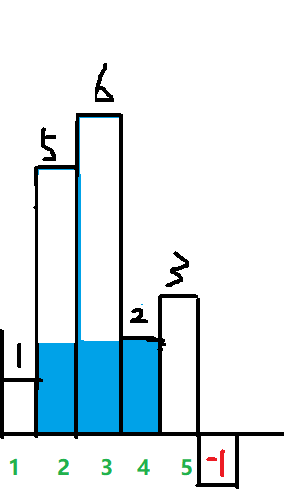




















 7780
7780

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








