深度学习入门——基于Python（更新中）

---

激活函数

① 阶跃函数

def step_function(x):
 	y = x > 0
 	return y.astype(np.int)

② sigmoid函数

def sigmoid(x):
 	return 1 / (1 + np.exp(-x))

③ ReLU函数

def relu(x):
 	return np.maximum(0, x)

④ softmax函数

# 此方法在计算时容易出现溢出现象
def softmax(x):
 	exp_x = np.exp(x)
 	sum_exp_x = np.sum(exp_x)
 	y = exp_x / sum_exp_x
	return y

def softmax(x):
 	c = np.max(x)
 	exp_x = np.exp(x - c) # 溢出对策
 	sum_exp_x = np.sum(exp_x)
 	y = exp_x / sum_exp_x
 	return y

---

输出层 激活函数选择

输出层所用的激活函数，要根据求解问题的性质决定。一般情况可按照如下选择：

① 恒等函数（回归问题）
② sigmoid函数（二分类）
③ softmax函数（多分类）

损失函数

神经网络以损失函数为线索寻找最优权重参数，这个损失函数可以使用任意函数，但一般用均方误差和交叉熵误差等。

均方误差

均方误差会计算神经网络的输出和正确解监督数据的各个元素之差的平方，再求总和。

公式：
其中yk是表示神经网络的输出，tk表示监督数据，k表示数据的维数。

def mean_squared_error(y, t):
 	return 0.5 * np.sum((y-t)**2)

交叉熵误差

实际上只计算对应正确解标签的输出的自然对数，也就是说，交叉熵误差的值是由正确解标签所对应的输出结果决定的

公式：
这里，log表示以e为底数的自然对数。yk是神经网络的输出，tk是正确解标签。并且，tk中只有正确解标签的索引为1，其他均为0（one-hot表示）

def cross_entropy_error(y, t):
 	delta = 1e-7 # 保护对策，防止出现负无穷大现象
 	return -np.sum(t * np.log(y + delta))

数值微分

定义导数

导数公式：
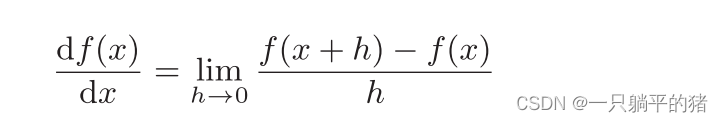根据公式编写导数代码：

def numerical_diff(f, x):
	h = 10e-50
	return (f(x+h) - f(x)) / h

但是，这段代码有两处需要改进的地方。

① 舍入误差。所谓舍入误差，是指因省略小数的精细部分的数值（比如，小数点第8位以后的数值）而造成最终的计算结果上的误差。比如 np.float32(1e-50)，结果显示 0.0。所以将微小值h改为10的−4次方。

② 与函数f的差分有关。为了减小这个误差，我们可以计算函数f在(x + h)和(x − h)之间的差分。因为这种计算方法以x为中心，计算它左右两边的差分，所以也称为中心差分（而(x + h)和x之间的差分称为前向差分）。

由此，上述代码可作如下修改：

def numerical_diff(f, x):
 	h = 1e-4 # 0.0001
 	return (f(x+h) - f(x-h)) / (2*h)