Ek求最大流

EK求最大流

---

题目描述

---

核心思路

残留网络：残留网络$G^{\ast }$与原网络$G$的节点相同，$G$中的每条边都对应$G^{\ast }$中的一条或两条边。在残留网络中，与原网络对应的同向边是可增量（还可以增加多少流量），反向边是实际流量。

在残留网络中不显示0流量边，网络$G$及可行流对应的残留网络$G^{\ast }$如下图：

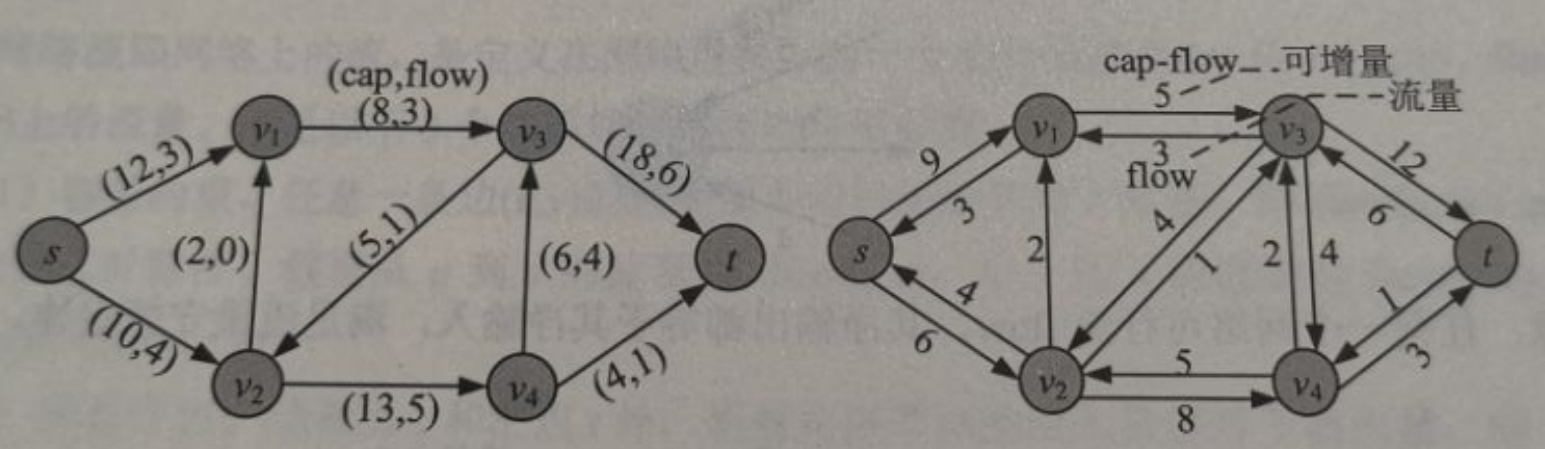
如下图所示，第一次从$v_1$到$v_3$流出了flow为6的流量，那么由于最大容量cap=10，那么下次还可以从$v_1$到$v_3$流出flow为$10-6=4$的流量。反向边是实际流量可以理解为：$v_1$后悔把6这个流量送给$v_3$了，然后$v_3$就又把6这个流量归还给了$v_1$。

增广路是指残留网络上从源点$S$到汇点$T$的一条简单路径。增广量是指增广路径上每条边都可以增流的最小值。

如下图所示，$s\to v_1\to v_3\to t$就是一条增广路，增广量是这条增广路径上各边的最小值$min(9,5,12)=5$。为什么是取5而不是取9或者12呢？因为比如假设从源点$S$流出了流量9，但是由于$v_1\to v_3$这条水管最多承受流量5，因此当我们把流量9送到这条水管时，这条水管就爆了，不能运输水了，因此是取这条增广路径上各边的最小值。

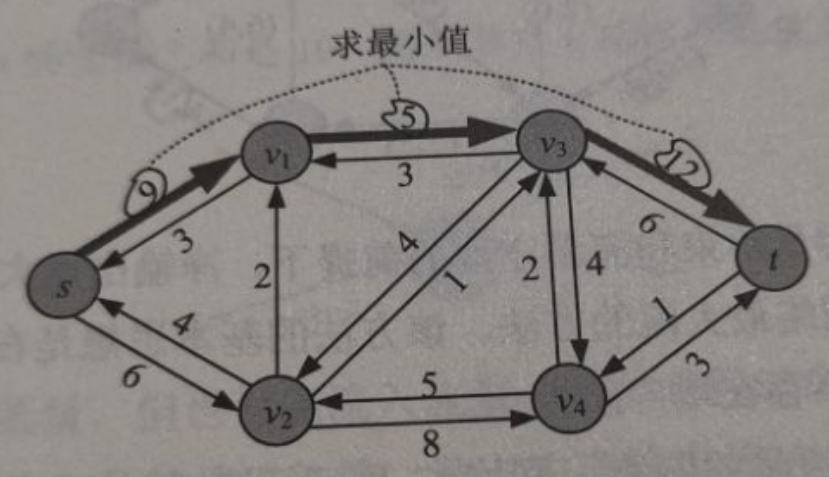
增广路定理：设$flow$是网络$G$的一个可行流，如果不存在从源点到汇点的增广路，则$flow$是$G$的一个最大流。

增广路算法的基本思想：在残留网络中寻找增广路，然后在实流网络中沿增广路增流，在残留网络中沿增广路减流，重复以上步骤，直到不存在增广路时为止。此时，实流网络中的可行流就是所求的最大流。

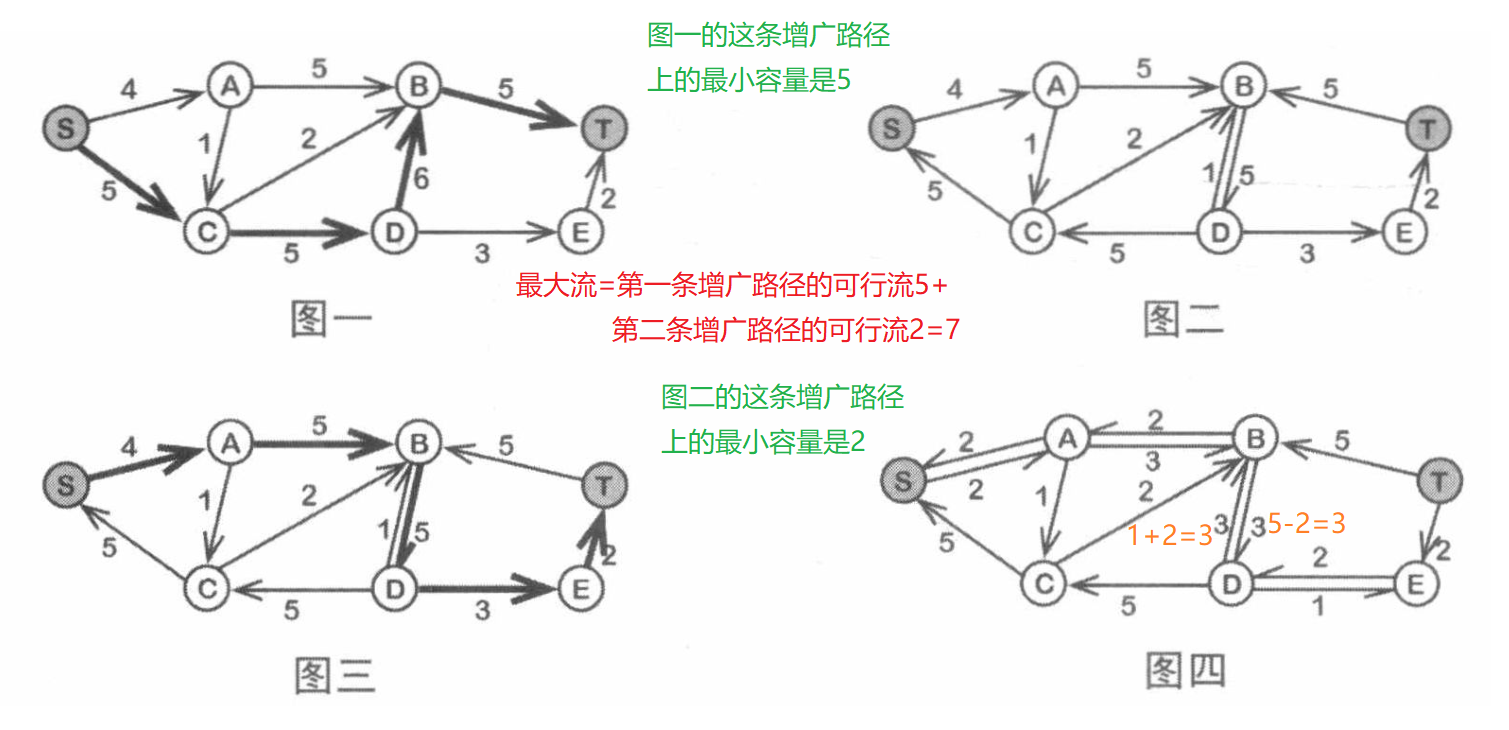
如上图所示。图一是原网络中每条边的初始容量。EK算法找到了流量为5的增广路$S\to C\to D\to B\to T$。于是在图二中，剩余容量对应发生了变化。接着，图三中，EK算法又找到了流量为2的增广路$S\to A\to B\to D\to E\to T$。最终在图四中，网络就不存在增广路了，最大流的大小就是$5+2=7$。图中省略了剩余容量为0的边。

问题：如何理解i=e[pre[i]^1]

如下图

啊

---

代码

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=1010,M=20010,INF=1e8;
int n,m,S,T;
//f是边上的容量
int h[N],e[M],ne[M],f[M],idx;
//q是宽搜存放点的队列
//d[i]=x表示从起点S到点i这条增广路上各边的最小剩余容量
//pre数组记录的前驱边而不是前驱点 比如pre[ver]=i表示节点ver是从边i走过来的
//即节点ver的前驱边是 边i
int q[N],d[N],pre[N];
//宽搜中判断某个点是否已经被访问过了
bool st[N];

void add(int a,int b,int c)
{
    //正向边 初始化还没有流出流量 所以正向边课流出的容量保持不变 仍为c
    e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
    //反向边 初始化还没有流出流量 所以反向边没有流量  仍为0
    e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;  
}

bool bfs()
{
    memset(st,0,sizeof st);
    int hh=0,tt=0;
    //由于d是想要求最小  所以一般初始化为无穷大
    q[0]=S,st[S]=true,d[S]=INF;
    //进行宽搜
    while(hh<=tt)
    {
        int t=q[hh++];  //取出队头元素
        //遍历节点t的所有邻接点
        for(int i=h[t];~i;i=ne[i])  //i是边
        {
            int ver=e[i];//ver是节点t的邻接点
            //如果节点ver还没有被访问过 并且i这条边的容量仍然是大于0
            if(!st[ver]&&f[i])
            {
                st[ver]=true;
                //d[t]表示从起点到节点t这条增广路径上的各边中的最小剩余容量
                //f[i]表示i这条边的容量
                //d[ver]表示从起点S到点ver这条增广路上各边的最小剩余容量
                d[ver]=min(d[t],f[i]);
                //pre[ver]=i表示节点ver是从边i走过来的 即节点ver的前驱边是 边i
                pre[ver]=i;
                //如果走到了终点  则找到了一条从起点S到终点S且容量>0的增广路径
                if(ver==T)
                    return true;
                q[++tt]=ver;
            }
        }
    }
    //没有找到增广路径
    return false;
}

int EK()
{
    int maxflow=0;  //最大流
    //如果一直能找到增广路径  则一直寻找 同时累加每一条增广路径上的d[T]
    //最终就是这张图的最大流
    while(bfs())
    {
        //累加不同的增广路径上的d[T]
        maxflow+=d[T];
        //从终点T逆向到起点S  更新正向边和反向边的容量
        for(int i=T;i!=S;i=e[pre[i]^1])
        {
            //由于已经流出了d[T],那么pre[i]这条边还可以流出f[pre[i]]-d[T]的流量
            f[pre[i]]-=d[T];    //更新正向边的容量
            f[pre[i]^1]+=d[T];  //更新反向边的容量
        }
    }
    //到这里说明不能再找到一条增广路径了  那么此时就求出了最大流
    return maxflow;
}

int main()
{
    memset(h,-1,sizeof h);
    scanf("%d%d%d%d",&n,&m,&S,&T);
    while(m--)
    {
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(a,b,c);
    }
    printf("%d\n",EK());
    return 0;
}

---