本文详细介绍了二叉树的几个关键概念，包括满二叉树、完全二叉树、BST树、平衡二叉树和对称二叉树。满二叉树是指除最后一层外，每层节点都满的二叉树；完全二叉树是满二叉树的一种特殊情况，最后一层从右向左可能缺失部分节点。BST树（二叉搜索树）要求节点的左子树所有节点小于父节点，右子树所有节点大于父节点。平衡二叉搜索树（AVL树）保证了左右子树的高度差不超过1。对称二叉树则指其镜像与自身相同。通过深入理解这些概念，有助于提升对二叉树的掌握。
二叉树中的判断有以下几种：
是否完全二叉树、是否满二叉树、是否为BST树、是否为平衡二叉树、是否为对称二叉树、完美二叉树
满二叉树：
除最后一层无任何子节点外，每一层上的所有结点都有两个子结点的二叉树。
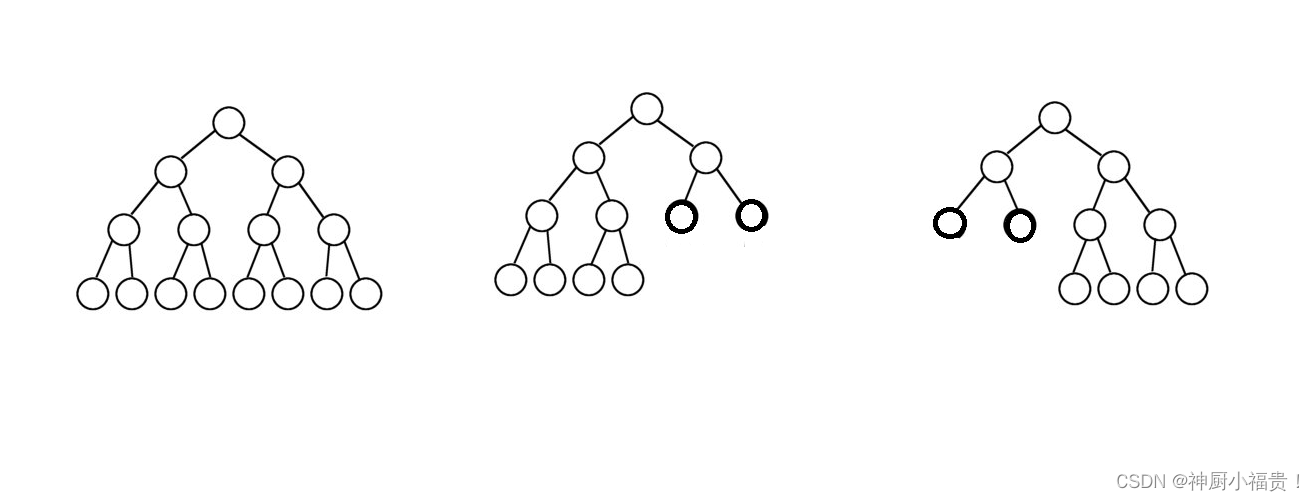
上述所示图除最外一层节点之外，每个节点都有两个子节点，所以上述两图都是满二叉树！！！
完全二叉树：
完全二叉树是满二叉树的一直特例，怎么个特例法呢？
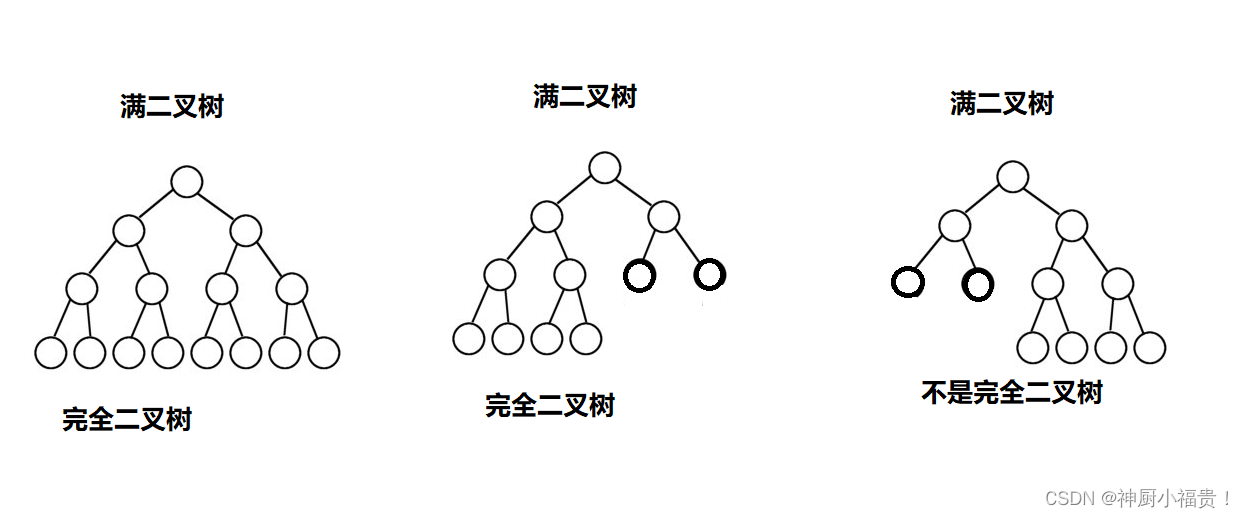
上图为啥有些是完全二叉树，有些又不是完全二叉树呢？
完全二叉树定义:完全二叉树(Complete Binary Tree):若设二叉树的高度为h。除第h层外，其它各层(0～h-1)的结点数都达到最大个数，第h层从右向左连续缺若干结点，这就是完全二叉树
上述所说从右向左缺若干节点，也就是说在h层的时候，如果有节点都在左半边，而缺的都是右半边的
最低0.47元/天 解锁文章
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
