时间复杂度与空间复杂度_空间复杂度 1e9-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_45829112/article/details/119509798

本文解析了斐波那契数列和二分查找的时间复杂度，前者为O(2^n)，后者为O(log N)。同时介绍了空间复杂度的概念，强调了在计算资源丰富的现代环境中，理解算法效率的重要性。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

先来说一下定义：

时间复杂度：计算的不是时间而是计算大概运行次数

空间复杂度：不计算空间而是计算大概定义的变量个数

时间复杂度：

就拿最经典的斐波那契数列和二分查找来说

以下代码就是斐波那契数列的时间复杂度的

long long Fibonacci(size_t N)
{
	return N < 2 ? N : Fibonacci(N - 1) + Fibonacci(N - 2);
}

自己画的，略微丑一些多多包涵

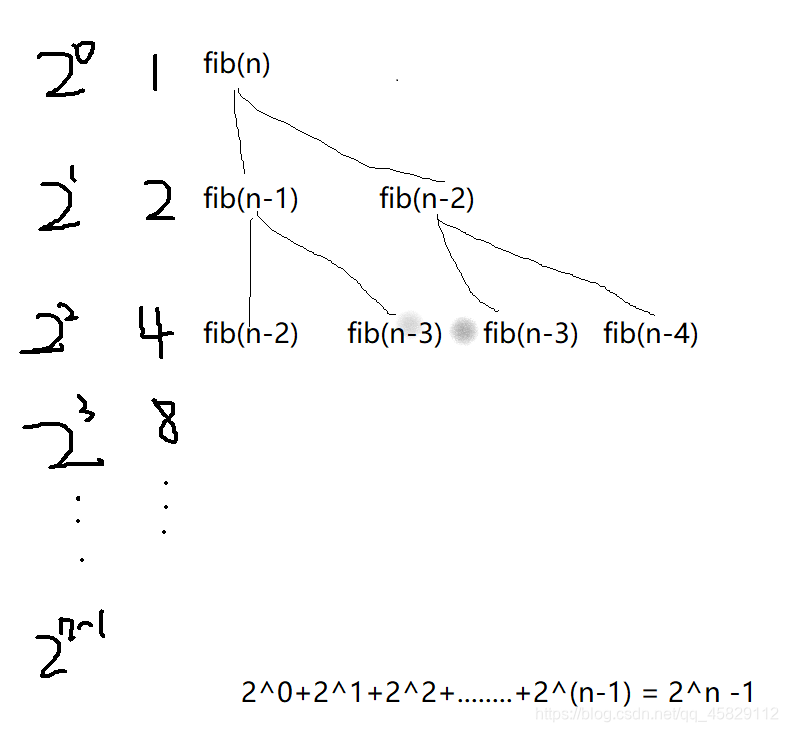
所以它的时间复杂度是O(2^n),根据大家电脑cpu的睿频，比如我的是2.60ghz，每秒可以跑26亿次，理论上来说，只要(2^n)小于26亿次在一秒内都是可以跑完的

二分查找：

mid = (left + right) / 2;
  if (x < mid)
  {
   right = mid;
  }
  else if (x > mid)
  {
   left = mid+1;
  }
  else 
  {
   printf("找到%d了\n", x);
   break;
  }

二分查找其实顾名思义就是一半的一半的一半.......一直找下去，直到找到那个数字，然后退出循环

刚开始有N个数，开始不断的循环N/2/2/2/2/2/2/2/2/2/2........直到只有一个数的时候，找到了，然后退出循环然后循环了x次，N=2^x 所以x = long以二为底N的对数，所以二分查找的时间复杂度就是O(long以二为底N的对数).

空间复杂度：就是在函数中数他有多少个变量就好

为什么不关注变量的类型呢，因为现在内存动不动8g 16g的转换成字节个数就是80亿 160亿字节，就比如你有这么多钱，每次花最多就像double类型的8块，最少char类型1块，对你来说没区别，你不需要关注每次花多少钱，只需要记住花了多少次就可以了

总结

时间复杂度搞清楚二分查找和斐波那契数列就可以了，还有一点值得注意一下，当运行次数为常数时，统一记作O(1),这就相当于默认只要是常数级别的运行次数，时间都是固定的！