LeetCode——#78 子集_c# 代码78子集 leecode-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_45827239/article/details/103476661

本文详细解析了LeetCode中#78子集问题的三种解法，包括递归迭代、回溯法和位掩码法，分别分析了每种方法的代码实现、结果和复杂度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

一、题目描述

给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。
说明：解集不能包含重复的子集。
示例:
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]

二、解题思路

方法一

递归迭代

使用数学的思维思考：

当nums=[]时，子集有一个，就是空集[]；
当nums=[A]时，子集有两个：空集[]和该元素的集合[A]，就是该元素与空集的并集；
当nums=[A, B]时，子集有四个：空集[]，两个元素分别的集合[A]、[B]，两个元素的并集[A, B]。
综上，可以总结出，一个集合的所有子集就是：其n-1个元素集合的子集分别与第n个元素组合所产生的集合，再与n-1个元素集合的子集所产生的并集。
编程思维就是递归迭代。

代码

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        List = [[]]
        for i in range(len(nums)):  # 遍历所有的元素
            for j in range(len(List)):  # 遍历所有子集元素
                List.append([nums[i]]+List[j])  # 组合元素
        return List

结果

在这里插入图片描述

复杂度分析:

时间复杂度：O(n!)
空间复杂度：O(1)

方法二（参考网上方法）

回溯

回溯法（单独讲解),待更新。

代码

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        List = [[]]
        n = len(nums)
        def track_back(i, temp):
            if i == n:
                return
            List.append(temp)
            for j in range(i+1, n):
                track_back(j, temp+[nums[j]])
        track_back(-1, [])
        return List

结果

在这里插入图片描述

复杂度分析

时间复杂度：O(n!)
空间复杂度：O(1)

方法三

位掩码

如下图，将元素组成子集对应到二级制数，，然后来取不同的子集。
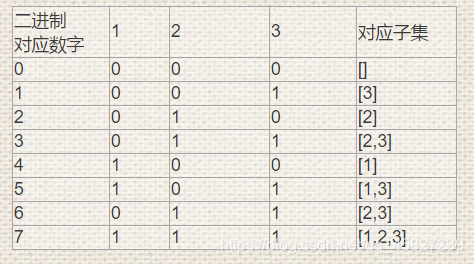
在这里插入图片描述

代码

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        List = []
        n = len(nums)
        for i in range(2**n):  # 子集个数2^n
            temp = []
            for j in range(n):
                if (i>>j)%2:  # 判断该位置是1或0，是否需要添加到子集
                    temp.append(nums[j])
            List.append(temp)
        return List