【数据结构】树——二叉树

二叉树

二叉树的定义

二叉树是另一种树型结构，其特点是每个结点至多只有俩棵子树（即二叉树中不存在度大于2的结点），并且二叉树的子树有左右子树之分，其次序不能任意颠倒。（简单来说，有序树，树的结点为0，1，2的树）
与树相似，二叉树也以递归的形式定义。二叉树是n（n>=0）个结点的有限集合，或者为空二叉树，即n=0，或者由一根结点和两个互不相交的称为根的左子树和右子树组成。左子树和右子树又分别是一棵二叉树。
二叉树是有序树，若将其左右子树颠倒，则成为另一棵不同的二叉树。即使树中结点只有一棵子树，也要区分它是左子树还是右子树。
二叉树与度为2的有序树的区别：

1. 度为2的树至少有三个结点，而二叉树可以为空。
2. 度为2的有序树的孩子的左右次序是相对于另一个孩子而言的，若某个结点只有一个孩子，则这个孩子就无需区分其左右次序，而二叉树无论其孩子是否为2，均需确定其左右次序，即二叉树的结点次序不是相对于零一结点而言的，而是确定的。

二叉树的性质

二叉树具有以下几个性质：

1. 二叉树中，第i层最多有2^（i-1）个结点。(i>=1)
2. 如果二叉树的深度为K,那么此二叉树最多有2^k -1个结点。
3. 二叉树中，终端结点数(叶子结点数)为n0,度为2的结点数为n2，则n0=n2+1。

性质3的计算方法为：对一个二叉树来说，除了度为0的叶子结点和度为2的结点，剩下的就是度为1的结点(设为n1)，那么总结点n=n0+n1+n2。

同时，对于每个结点来说都是其父结点分支表示的，假设树中分支数为B，那么总结点数n=B+1。而分支数是可以通过n1和n2表示的，即B=n1+2*n2。所以，n用另外一种方式表示n=n1+2*n2+1。

俩种方式得到的n值组成一个方程组，就可以得出n0=n2+1。

二叉树还可以继续分类，衍生出满二叉树和完全二叉树。

满二叉树

如果二叉树除了叶子结点，每个结点的度都为2，则此二叉树称为满二叉树。

满二叉树除了满足普通二叉树的性质，还具有以下性质：

1. 满二叉树中第i层的结点数为2^(n-1)个。
2. 深度为k的满二叉树必有2^k -1个结点，叶子数为2^(k-1)。
3. 满二叉树中不存在度为1的结点，每个分支结点中都有俩棵深度相同的子树，且叶子结点都在最底、层。
4. 具有n个结点的满二叉树的深度为${\log }_2(n+1)$

完全二叉树

如果二叉树中除去最后一层结点，为满二叉树，最后一层结点依次从左到右分布，则此二叉树被称为完全二叉树。

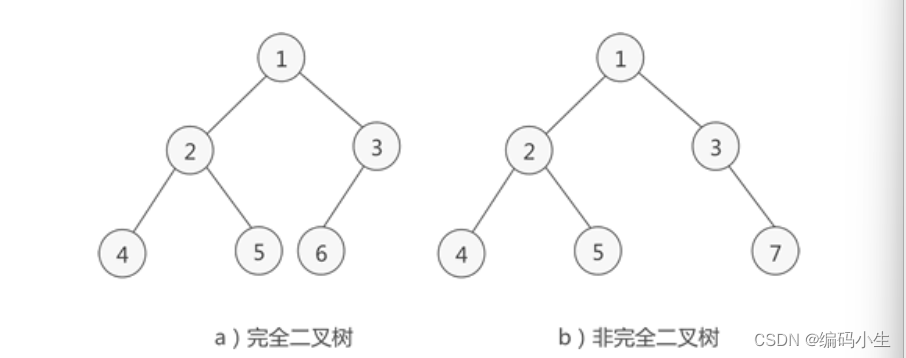
如图所示a)是一棵完全二叉树，b)由于最后一层的结点没有按照从左向右分布，因此只能算作普通的二叉树。
完全二叉树除了具有普通二叉树的性质，它自身也具有一些独特的性质，比如说，n个结点的完全二叉树的深度为$\lfloor {\log }_{2}n\rfloor$+1。
$\lfloor {\log }_{2}n\rfloor$ 表示取小于${\log }_{2}n$的最大整数。例如$\lfloor {\log }_{2}4\rfloor$=2，而$\lfloor {\log }_{2}5\rfloor$的结果也是2.

对任意一个完全二叉树来说，如果将含有的结点按照层次从左到右依次标号
对于任意一个结点i，完全二叉树还有以下几个结论成立：

1. 当i>1时，父结点为结点[i/2]。(i=1,表示的是根节点，无父结点)
2. 如果2i>n(总结点的个数)，则结点i肯定没有左孩子(为叶子结点)；否则其左孩子是结点2i。
3. 如果2i+1>n，则结点i肯定没有右孩子；否则右孩子是结点2i+1。

平衡二叉树：树上任一结点的左子树和右子树的深度之差不超过1。

二叉树存储结构

二叉树的顺序存储结构

二叉树的顺序存储结构，指的是使用顺序表(数组)存储二叉树。需要注意的是顺序存储只适用于完全二叉树，换句话说，只有完全二叉树才可以使用顺序表存储。因此，如果我们想要顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树。
满二叉树也可以使用顺序存储。满二叉树也是完全二叉树。因为它满足完全二叉树的所有特征。

普通二叉树转化为完全二叉树的方法很简单，只需给二叉树额外添加一些结点，将其拼凑成完全二叉树即可。

图1中，左侧是普通二叉树，右侧是转化后的完全(满)二叉树。
完全二叉树的顺序存储，仅需从根节点开始，按照层次依次将树中结点存储到数组中即可。

同样，存储由普通二叉树转换来的完全二叉树也是如此。例如下图为普通二叉树的数组存储状态图。

由此我们就是实现了完全二叉树的顺序存储。
从顺序表中还原二叉树：完全二叉树具有这样的性质，将树中结点按照层次并从左到右依次标号（1，2，3.……）,若结点i有左右孩子，则左孩子结点为2i,右孩子结点为2i+1。此性质可用于还原数组中存储的完全二叉树，也就是实现图3到图2，由图4到图1的转变。

二叉树的链式存储

由上述二叉树的顺序存储，会发现二叉树其实并不适合用数组存储，因为从不是每个二叉树都是完全二叉树，普通二叉树使用顺序表村春或多或少会存在空间浪费的现象。因此二叉树一般常采用链式存储结构，用链表结点来存储二叉树中的每一个结点。在二叉树中，结点结构通常包括若干数据域，二叉链表至少包含3个域：数据域data，左指针域lchild和右指针域rchild，

如图1所示，此为一棵普通的二叉树，若将其采用链式存储，则只需从树的根结点开始，将各个结点及其左右孩子使用链表存储即可。

图1对应的链式存储结构如图2所示,采用链式存储二叉树时，其节点结构由三部分构成：

• 指向左孩子节点的指针(lchild)；
• 节点存储的数据(data);
• 指向右孩子节点的指针(rchild);