Introduction
PCA的目的是要将原有数据投影到新的空间,通过观察全局数据特点对数据赋予新的属性后进行转换,做到降维的同时尽可能增加数据的区分度。
数据投影
假设现在有样本数据object
x
x
x和投影方向向量
w
w
w,
z
=
w
⋅
x
z=w\cdot x
z=w⋅x则代表着将object投影到该方向上,其中
w
w
w作为方向向量其长度为1(
∣
∣
w
∣
∣
2
=
1
||w||_2=1
∣∣w∣∣2=1)。经过计算,每个object在这个方向上都有一个scalar,那么这个投影方向可以用来区分不同object,也就可以作为一个attribute dimension。

PCA通过寻找最优的方向,能够最大程度上区分样本数据,通常方向也不止一个,且各个方向保持垂直进而形成新的空间。
衡量标准
投影方向
w
w
w的好坏,通过所有object经过投影之后得到的分布来衡量,分布散意味着经过这个投影后不同样本点之间可以较好的区别。

通过投影后数据的variance代表这一标准的量化:
V
a
r
(
z
)
=
1
N
∑
z
(
z
−
z
ˉ
)
2
Var(z)=\frac{1}{N}\sum\limits_{z}(z-\bar{z})^2
Var(z)=N1z∑(z−zˉ)2
Calculation
将单个数据样本投影到新空间:
z
=
W
x
z=Wx
z=Wx
-
x
x
x表示单个原有数据样本
- x = [ x 1 x 2 ⋮ x m ] x=\left[ \begin{matrix} x_1 \\ x_2\\ \vdots\\ x_m\end{matrix} \right] x=⎣⎢⎢⎢⎡x1x2⋮xm⎦⎥⎥⎥⎤ ( m × 1 m×1 m×1)
-
W
W
W表示映射矩阵
- W = [ ( w 1 ) ⊺ ( w 2 ) ⊺ ⋮ ( w n ) ⊺ ] W=\left[ \begin{matrix} (w^1)^\intercal \\ (w^2)^\intercal\\ \vdots\\ (w^n)^\intercal\end{matrix} \right] W=⎣⎢⎢⎢⎡(w1)⊺(w2)⊺⋮(wn)⊺⎦⎥⎥⎥⎤( n × m n×m n×m)
- w i w^i wi:映射方向,两两正交,因此 W W W是正交矩阵(orthogonal matrix)
-
z
z
z表示将
x
x
x映射到新空间的位置
- z = [ z 1 z 2 ⋮ z n ] z=\left[ \begin{matrix} z_1 \\ z_2\\ \vdots\\ z_n\end{matrix} \right] z=⎣⎢⎢⎢⎡z1z2⋮zn⎦⎥⎥⎥⎤ ( n × 1 n×1 n×1)
- z 1 = w 1 ⋅ x z_1=w^1\cdot x z1=w1⋅x表示 x x x在 w 1 w^1 w1方向上的投影, z 2 = w 2 ⋅ x z_2=w^2\cdot x z2=w2⋅x表示 x x x在 w 2 w^2 w2方向上的投影,… …
Lagrange multiplier
求解PCA有现成的函数可以调用,也可以把PCA描述成neural network用gradient descent的方法求解,这里用拉格朗日乘数法(Lagrange multiplier)求解PCA。
w 1 w^1 w1计算过程
- 计算
z
1
ˉ
\bar{z_1}
z1ˉ:
z 1 = w 1 ⋅ x z 1 ˉ = 1 N ∑ z 1 = 1 N ∑ w 1 ⋅ x = w 1 ⋅ 1 N ∑ x = w 1 ⋅ x ˉ \begin{aligned} &z_1=w^1\cdot x\\ &\bar{z_1}=\frac{1}{N}\sum z_1=\frac{1}{N}\sum w^1\cdot x=w^1\cdot \frac{1}{N}\sum x=w^1\cdot \bar x \end{aligned} z1=w1⋅xz1ˉ=N1∑z1=N1∑w1⋅x=w1⋅N1∑x=w1⋅xˉ
- 计算
V
a
r
(
z
1
)
Var(z_1)
Var(z1):
V a r ( z 1 ) = 1 N ∑ z 1 ( z 1 − z 1 ˉ ) 2 = 1 N ∑ x ( w 1 ⋅ x − w 1 ⋅ x ˉ ) 2 = 1 N ∑ ( w 1 ⋅ ( x − x ˉ ) ) 2 = 1 N ∑ ( w 1 ) T ( x − x ˉ ) ( x − x ˉ ) T w 1 = ( w 1 ) T 1 N ∑ ( x − x ˉ ) ( x − x ˉ ) T w 1 = ( w 1 ) T C o v ( x ) w 1 \begin{aligned} Var(z_1)&=\frac{1}{N}\sum\limits_{z_1} (z_1-\bar{z_1})^2\\ &=\frac{1}{N}\sum\limits_{x} (w^1\cdot x-w^1\cdot \bar x)^2\\ &=\frac{1}{N}\sum (w^1\cdot (x-\bar x))^2\\ &=\frac{1}{N}\sum(w^1)^T(x-\bar x)(x-\bar x)^T w^1\\ &=(w^1)^T\frac{1}{N}\sum(x-\bar x)(x-\bar x)^T w^1\\ &=(w^1)^T Cov(x)w^1 \end{aligned} Var(z1)=N1z1∑(z1−z1ˉ)2=N1x∑(w1⋅x−w1⋅xˉ)2=N1∑(w1⋅(x−xˉ))2=N1∑(w1)T(x−xˉ)(x−xˉ)Tw1=(w1)TN1∑(x−xˉ)(x−xˉ)Tw1=(w1)TCov(x)w1
-
C
o
v
(
x
)
=
1
N
∑
(
x
−
x
ˉ
)
(
x
−
x
ˉ
)
T
Cov(x)=\frac{1}{N}\sum(x-\bar x)(x-\bar x)^T
Cov(x)=N1∑(x−xˉ)(x−xˉ)T,定常矩阵
- 对称(symmetric)
- 半正定(positive-semidefine)
- 非负(non-negative)特征值(eigenvalues)
- 目标函数:
arg max w 1 V a r ( z 1 ) = ( w 1 ) T C o v ( x ) w 1 s . t . ∣ ∣ w 1 ∣ ∣ 2 = 1 {\underset {w^1}{\operatorname {arg\ max} }}\,Var(z_1) =(w^1)^T Cov(x)w^1\\ s.t. \ \ \ ||w^1||_2=1 w1arg maxVar(z1)=(w1)TCov(x)w1s.t. ∣∣w1∣∣2=1
- ∣ ∣ w 1 ∣ ∣ 2 = ( w 1 ) T w 1 ||w^1||_2=(w^1)^Tw^1 ∣∣w1∣∣2=(w1)Tw1
- 拉格朗日乘数法构造函数:
g ( w 1 ) = ( w 1 ) T S w 1 − α ( ( w 1 ) T w 1 − 1 ) g(w^1)=(w^1)^TSw^1-\alpha((w^1)^Tw^1-1) g(w1)=(w1)TSw1−α((w1)Tw1−1)
- S = C o v ( x ) S=Cov(x) S=Cov(x),定常矩阵
- 拉格朗日乘数法求极值:
-
对 w 1 w^1 w1 vector中每一个element做偏微分:
∂ g ( w 1 ) / ∂ w 1 1 = 0 ∂ g ( w 1 ) / ∂ w 2 1 = 0 ∂ g ( w 1 ) / ∂ w 3 1 = 0 . . . \partial g(w^1)/\partial w_1^1=0\\ \partial g(w^1)/\partial w_2^1=0\\ \partial g(w^1)/\partial w_3^1=0\\ ... ∂g(w1)/∂w11=0∂g(w1)/∂w21=0∂g(w1)/∂w31=0... -
整理上述推导式,可以得到 w 1 w^1 w1是S的特征向量(eigenvector):
S w 1 = α w 1 Sw^1=\alpha w^1 Sw1=αw1 -
带入目标函数:
( w 1 ) T S w 1 = ( w 1 ) T α w 1 = α ( w 1 ) T w 1 = α (w^1)^TSw^1=(w^1)^T \alpha w^1=\alpha (w^1)^T w^1=\alpha (w1)TSw1=(w1)Tαw1=α(w1)Tw1=α
- 结论
maximize ( w 1 ) T S w 1 (w^1)^TSw^1 (w1)TSw1的问题转化为maximize α \alpha α,那矩阵 S S S的特征值 α \alpha α最大时对应的那个特征向量 w 1 w^1 w1就是目标向量。也就是说 w 1 w^1 w1是 S = C o v ( x ) S=Cov(x) S=Cov(x)这个matrix中的特征向量,对应最大的特征值 λ 1 \lambda_1 λ1。
w 2 w^2 w2计算过程
- 目标函数:
arg max w 2 V a r ( z 2 ) = ( w 2 ) T C o v ( x ) w 2 s . t . ( w 2 ) T w 2 = 1 ( w 2 ) T w 1 = 0 {\underset {w^2}{\operatorname {arg\ max} }}\,Var(z_2) =(w^2)^T Cov(x)w^2\\ s.t. \ \ \ (w^2)^Tw^2=1\\ \ \ \ \ \ \ \ \ \ (w^2)^Tw^1=0 w2arg maxVar(z2)=(w2)TCov(x)w2s.t. (w2)Tw2=1 (w2)Tw1=0
- 不仅需要限制 w 2 w^2 w2长度为1,同时 w 2 w^2 w2和 w 1 w^1 w1需保持正交(orthogonal)
- 拉格朗日乘数法构造函数:
g ( w 2 ) = ( w 2 ) T S w 2 − α ( ( w 2 ) T w 2 − 1 ) − β ( ( w 2 ) T w 1 − 0 ) g(w^2)=(w^2)^TSw^2-\alpha((w^2)^Tw^2-1)-\beta((w^2)^Tw^1-0) g(w2)=(w2)TSw2−α((w2)Tw2−1)−β((w2)Tw1−0)
- 拉格朗日乘数法求极值:
-
对 w 2 w^2 w2 vector中每一个element做偏微分:
∂ g ( w 2 ) / ∂ w 1 2 = 0 ∂ g ( w 2 ) / ∂ w 2 2 = 0 ∂ g ( w 2 ) / ∂ w 3 2 = 0 . . . \partial g(w^2)/\partial w_1^2=0\\ \partial g(w^2)/\partial w_2^2=0\\ \partial g(w^2)/\partial w_3^2=0\\ ... ∂g(w2)/∂w12=0∂g(w2)/∂w22=0∂g(w2)/∂w32=0... -
整理后得到:
S w 2 − α w 2 − β w 1 = 0 Sw^2-\alpha w^2-\beta w^1=0 Sw2−αw2−βw1=0 -
上式两侧同乘 ( w 1 ) T (w^1)^T (w1)T,得到:
( w 1 ) T S w 2 − α ( w 1 ) T w 2 − β ( w 1 ) T w 1 = 0 (w^1)^TSw^2-\alpha (w^1)^Tw^2-\beta (w^1)^Tw^1=0 (w1)TSw2−α(w1)Tw2−β(w1)Tw1=0 -
带入限制条件 ( w 2 ) T w 2 = 1 (w^2)^Tw^2=1 (w2)Tw2=1和 ( w 2 ) T w 1 = 0 (w^2)^Tw^1=0 (w2)Tw1=0,得到:
( w 1 ) T S w 2 − β = 0 (w^1)^TSw^2-\beta=0 (w1)TSw2−β=0 -
对 ( w 1 ) T S w 2 (w^1)^TSw^2 (w1)TSw2做transpose:
( w 1 ) T S w 2 = ( ( w 1 ) T S w 2 ) T = ( w 2 ) T S T w 1 = ( w 2 ) T S w 1 ( 注 : S T = S ) \begin{aligned} (w^1)^TSw^2&=((w^1)^TSw^2)^T\\ &=(w^2)^TS^Tw^1\\ &=(w^2)^TSw^1\ \ \ \ \ \ (注:S^T=S) \end{aligned} (w1)TSw2=((w1)TSw2)T=(w2)TSTw1=(w2)TSw1 (注:ST=S) -
w 1 w^1 w1满足 S w 1 = λ 1 w 1 Sw^1=\lambda_1 w^1 Sw1=λ1w1,代入上式:
( w 1 ) T S w 2 = ( w 2 ) T S w 1 = λ 1 ( w 2 ) T w 1 = 0 \begin{aligned} (w^1)^TSw^2&=(w^2)^TSw^1\\ &=\lambda_1(w^2)^Tw^1\\ &=0 \end{aligned} (w1)TSw2=(w2)TSw1=λ1(w2)Tw1=0 -
( w 1 ) T S w 2 = 0 (w^1)^TSw^2=0 (w1)TSw2=0, ( w 1 ) T S w 2 − β = 0 (w^1)^TSw^2-\beta=0 (w1)TSw2−β=0,得到:
β = 0 \beta=0 β=0 -
拉格朗日求极值公式 S w 2 − α w 2 − β w 1 = 0 Sw^2-\alpha w^2-\beta w^1=0 Sw2−αw2−βw1=0变为 S w 2 − α w 2 = 0 Sw^2-\alpha w^2=0 Sw2−αw2=0,即:
S w 2 = α w 2 Sw^2=\alpha w^2 Sw2=αw2
- 结论
- 与 w 1 w^1 w1一样, w 2 w^2 w2也是矩阵S的一个特征向量
- 并且由于 S S S是symmetric的,在不与 w 1 w_1 w1冲突的情况下, α \alpha α选取第二大的特征值 λ 2 \lambda_2 λ2时,可以使 ( w 2 ) T S w 2 (w^2)^TSw^2 (w2)TSw2最大
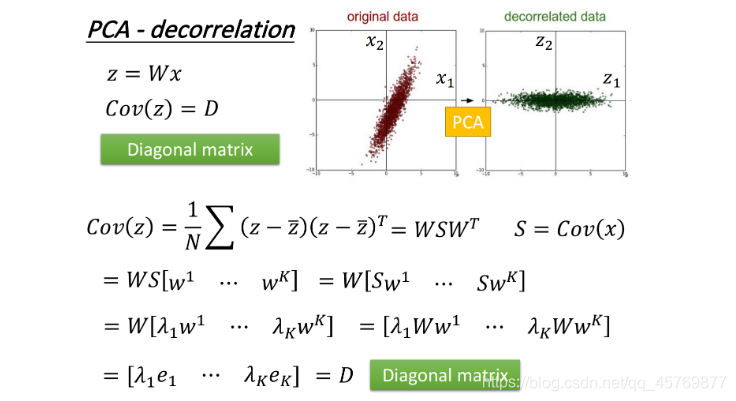
PCA-decorrelation
PCA可以使不同的方向 w w w之间的covariance变为0,也就是不同的属性之间是没有任何联系,这样可以最大化不同 w w w差异度,防止属性功能的重叠,从而减少arrribute vector的dimensoin数量,减少model所需的参数量。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








