PCA（part Ⅱ）

---

Reconstruction Component

可以把手写数字识别中的数字看做是由类似于笔画的basic component组成的，这个basic component set包含了能够构成所有数字的基本笔画。也就是说，basic component集合代表着数字所具有的所有基本特征，每个数字由这些基本特征组成，具有或不具有某个特征。

---

已知basic component set $\left[\begin{array}{c}{u}^1{u}^2{u}^3...u^k\end{array}\right]$，则手写数字图片$x$的表达式：
$$x\approx c_1{u}^1+c_2{u}^2+...+c_k{u}^k+\bar{x}$$

• $\left[\begin{array}{c}{c}_1{c}_2{c}_3...c_k\end{array}\right]$表示图像$x$在每个basic component上的权值
• $\bar{x}$表示所有image的平均值

---

例如假设手写数字识别的basic component set是$\left[\begin{array}{c}{u}^1{u}^2{u}^3{u}^4{u}^5\end{array}\right]$，对于手写数字7来说它可以用$u^1、u^3、u^5$组合而成，那$\left[\begin{array}{c}{c}_1{c}_2{c}_3{c}_4{c}_5\end{array}\right]=\left[\begin{array}{c}10101\end{array}\right]$，最终表达式$x=u^1+u^3+u^5$。

---

Reconstruction error

• 经basic component重构后的图片与实际图片存在误差。假设经basic component重构得到图像$\hat{x}$:
  $$\hat{x}=c_1{u}^1+c_2{u}^2+...+c_k{u}^k$$
• 重构图片$\hat{x}$与实际图片$x$的关系：
  $$x-\bar{x}\approx c_1{u}^1+c_2{u}^2+...+c_k{u}^k=\hat{x}$$
• Reconstruction error：
  $$||(x-\bar{x})-\hat{x}|{|}_2$$

---

Reconstruction Component

如果basic component已知，以basic component为model，对$\left[\begin{array}{c}{c}_1{c}_2{c}_3...c_k\end{array}\right]$的每个element进行梯度下降或直接计算总可以找到最贴近于真实图片的重构图像。但实际上这些basic component并不已知，我们目的是找到basic component。

• 目标函数：
  $$\begin{gathered} \bar{x}=\sum _{i=1}^k{c}_i{u}^i \\ \underset{u^1,u^2...,u^k}{\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{m}\mathrm{i}\mathrm{n}}\sum ||(x-\bar{x})-\hat{x}|{|}_2 \end{gathered}$$

---

Reconstruction Component矩阵表示

$$\begin{array}{rl}& x-\bar{x}\approx \left[\begin{array}{c}{u}_1{u}_2...u_k\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ ...\\ c_k\end{array}\right]\end{array}$$

• component $u_i$为列向量，其维度与原始图像$x$维度相同
• weight $c_i$为标量
  $$\begin{array}{rl}& x-\bar{x}\approx \left[\begin{array}{c}{u}_1^1{u}_2^1...u_k^1\\ u_1^2{u}_2^2...u_k^2\\ ...\\ u_1^n{u}_2^n...u_k^n\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ ...\\ c_k\end{array}\right]\end{array}$$
• 将component展开，上标标识不同vector，下标表示vector中的element

$$\begin{array}{rl}& \left[\begin{array}{c}{x}_1-\bar{x}\\ x_2-\bar{x}\\ ...\\ x_n-\bar{x}\end{array}\right]\approx \left[\begin{array}{c}{u}_1^1{u}_2^1...u_k^1\\ u_1^2{u}_2^2...u_k^2\\ ...\\ u_1^n{u}_2^n...u_k^n\end{array}\right]\left[\begin{array}{c}{c}_1^1{c}_1^2...c_1^n\\ c_2^1{c}_2^2...c_2^n\\ ...\\ c_k^1{c}_k^2...c_k^n\end{array}\right]\end{array}$$

• 多数据重构表示，共有$n$个object，用$k$个component表示

---

SVD（奇异值分解）

Reconstruction Component矩阵

SVD

• 可以使用SVD将每个matrix $X_{m\times n}$都拆成matrix $U_{m\times k}$、${\Sigma }_{k\times k}$、$V_{k\times n}$的乘积，其中k为component的数目
• 使用SVD拆解后的三个矩阵相乘，是跟等号左边的矩阵$X$最接近的，此时$U$就对应着$u^i$那部分的矩阵，$\Sigma \cdot V$就对应着$c_k^i$那部分的矩阵
• 根据SVD的结论，组成矩阵$U$的k个列向量(标准正交向量, orthonormal vector)就是$X{X}^T$最大的k个特征值(eignvalue)所对应的特征向量(eigenvector)，而$X{X}^T$实际上就是$x$的covariance matrix，因此$U$就是PCA的k个解
• 因此我们可以发现，通过PCA找出来的Dimension Reduction的transform，实际上就是把$X$拆解成能够最小化Reconstruction error的component的过程，通过PCA所得到的$w^i$就是component $u^i$，而Dimension Reduction的结果就是参数$c_i$
• 简单来说就是，用PCA对$x$进行降维的过程中，我们要找的投影方式$w^i$就相当于恰当的组件$u^i$，投影结果$z^i$就相当于这些组件各自所占的比例$c_i$

结论：用PCA找出来的投影方向 { w 1 , w 2 , . . . , w k } \{w^1,w^2,...,w^k\} {w1,w2,...,wk}就是Reconstruction Component { u 1 , u 2 , . . . , u k } \{u^1,u^2,...,u^k\} {u1,u2,...,uk}

PCA in Neuron Network

假设用PCA或SVD找到了$k$个最优投影方向 { w 1 , w 2 , . . . , w k } \{w^1,w^2,...,w^k\} {w1,w2,...,wk}，由
$$\begin{array}{rl}& x-\bar{x}=\left[\begin{array}{c}{u}_1{u}_2...u_k\end{array}\right]\left[\begin{array}{c}{c}_1\\ c_2\\ ...\\ c_k\end{array}\right]\end{array}$$
得到object在新空间上的投影（或者说在component上的权值）
$$\begin{array}{rl}& \left[\begin{array}{c}{c}_1\\ c_2\\ ...\\ c_k\end{array}\right]=(x-\bar{x})\left[\begin{array}{c}{u}_1{u}_2...u_k\end{array}\right]\end{array}$$
上述矩阵计算过程可以被表示成NN，其形式如下图。

矩阵计算的NN表示

training method—Autoencoder

此时，PCA就被表示成了只含一层hidden layer的神经网络，hidden layer是线性的激活函数，hidden layer的输入权值是投影方向，hidden layer的输出相当于对object进行编码，训练目标是让这个NN的input $x-\bar{x}$与output $\hat{x}$越接近越好，这件事就叫做Autoencoder（训练一个model，让它的输入等于输出，取出中间的某个隐藏层作为降维的结果）。

PCA与RNN的区别

通过PCA求解出的$w^i$与直接对上述的神经网络做梯度下降所解得的$w^i$是会不一样的，因为PCA解出的$w^i$是相互垂直的(orgonormal)，而用NN的方式得到的解无法保证$w^i$相互垂直，NN无法做到Reconstruction error比PCA小，因此：

• 在linear的情况下，直接用PCA找$W$远比用神经网络的方式更快速方便
• 用NN的好处是，它可以使用不止一层hidden layer，它可以做deep autoencoder

Weakness of PCA

PCA有很明显的弱点：

1. PCA属于unsupervised，它单纯依据数据分布找出特征（LDA是考虑了labeled data后进行降维，但属于supervised）。

2. PCA是linear的，对于图中的彩色曲面，PCA只能做到把这个曲面打扁压在平面上，我们期望把它平铺拉直进行降维，但这是一个non-linear的投影转换，对类似曲面空间的降维投影，需要用到non-linear transformation。

PCA Example

PCA—Pokemon

假设总共有800只宝可梦，每只都是一个六维度的样本点，即vector={HP, Atk, Def, Sp Atk, Sp Def, Speed}。宝可梦样本数据的$Cov(x)$是6维，最多可以投影到6维空间，可以先找出6个特征向量和对应的特征值${\lambda }_i$，其中${\lambda }_i$表示第i个投影维度的variance有多大，然后我们就可以计算出每个${\lambda }_i$的比重ratio=$\frac{{\lambda }_i}{\sum _{i=1}^6{\lambda }_i}$。

从上图的ratio可以看出${\lambda }_5$、${\lambda }_6$所占比例不高，即第5和第6个principle component(可以理解为维度)的影响比较小，用这两个dimension做投影所得到的variance很小，投影在这两个方向上的点比较集中，无法对区分宝可梦的特性做出太大的贡献，所以我们只需要利用前4个principle component即可。

新的维度上就是旧的维度的加权矢量和，从PC1到PC4这4个principle component都是6维度加权的vector，它们代表某种特性。

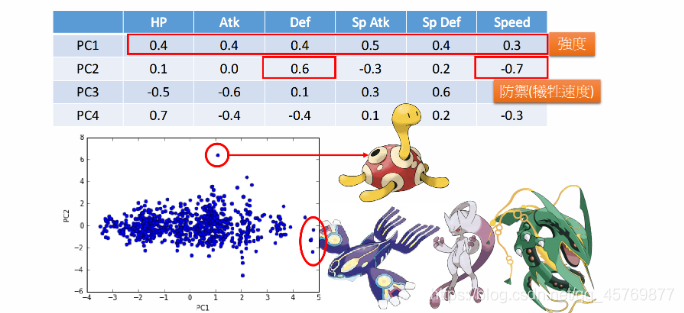
• PC1来说，每个值都是正的，因此这个组件在某种程度上代表了宝可梦的强度

• PC2来说，防御力Def很大而速度Speed很小，这个组件可以增加宝可梦的防御力但同时会牺牲一部分的速度

PCA—MNIST

对28×28的$Cov(x)=\frac{1}{N}\sum (x-\bar{x})(x-\bar{x}{)}^T$取前30个最大的特征值对应的特征向量。

PCA—Face

对$Cov(x)$取前30个最大的特征值对应的特征向量。

NMF

NMF(non-negative matrix factorization)，非负矩阵分解。PCA可以看成对原始矩阵$X$做SVD进行矩阵分解，但并不保证分解后矩阵的正负，实际上当进行图像处理时，如果部分组件的matrix包含一些负值的话，如何处理负的像素值也会成为一个问题(归一化处理比较麻烦)。

NMF on MINST

NMF on Face

NMF的基本精神是，强迫使所有组件和它的加权值都必须是正的，也就是说**所有图像都必须由组件叠加得到**。

More Related Approaches

降维的方法有很多，这里列举一些与PCA有关的方法：

• Multidimensional Scaling (MDS) [Alpaydin, Chapter 6.7]

  MDS不需要把每个data都表示成feature vector，只需要知道特征向量之间的distance，就可以做降维，PCA保留了原来在高维空间中的距离，在某种情况下MDS就是特殊的PCA

• Probabilistic PCA [Bishop, Chapter 12.2]

  PCA概率版本

• Kernel PCA [Bishop, Chapter 12.3]

  PCA非线性版本

• Canonical Correlation Analysis (CCA) [Alpaydin, Chapter 6.9]

  CCA常用于两种不同的data source的情况，比如同时对声音信号和唇形的图像进行降维

• Independent Component Analysis (ICA)

  ICA常用于source separation，PCA找的是正交的组件，而ICA则只需要找“独立”的组件即可

• Linear Discriminant Analysis (LDA) [Alpaydin, Chapter 6.8]

  LDA是supervised的方式