文章目录
AdaGrad
θ t + 1 = θ t − η σ t g t σ t = ∑ i = 0 t ( g i ) 2 \theta^{t+1}=\theta^t-\frac{\eta}{\sigma^t}g^t\\ \sigma^t=\sqrt{\sum\limits_{i=0}^t(g^i)^2} θt+1=θt−σtηgtσt=i=0∑t(gi)2
- learning rate设置为一个固定的初始值 η \eta η 除以一个变化的值 σ \sigma σ
- σ \sigma σ是对过程中所有梯度的平方和求根
Adagrad的特性:(Review Gradient Descent)
① 步伐逐步平坦
②考虑历史梯度,造成反差效果
③估测二次微分值,寻找最优参数更新
RMSProp
w t + 1 = w t − η σ t g t σ t = α ( σ t − 1 ) 2 + ( 1 − α ) ( g t ) 2 w^{t+1}=w^t-\frac{\eta}{\sigma^t}g^t \\ \sigma^t=\sqrt{\alpha(\sigma^{t-1})^2+(1-\alpha)(g^t)^2} wt+1=wt−σtηgtσt=α(σt−1)2+(1−α)(gt)2
-
learning rate设置为一个固定的初始值 η \eta η 除以一个修正值 σ \sigma σ
-
σ \sigma σ是对上一个 σ \sigma σ和当前梯度 g g g的平方加权后求根(特别的, σ 0 \sigma^0 σ0取 g 0 g^0 g0即可)
RMSProp和Adagrad的区别
Adagrad的 σ \sigma σ是对过程中所有的gradient取平方和求根,也就是说Adagrad考虑的是整个过程平均的gradient信息;RMSProp跟Adagrad不同之处在于,虽然RMSProp也是对所有的gradient进行平方和求根,但是它用权值 α \alpha α来调整对历史gradient还是当下gradient的偏重,如果你把α的值设的小一点,意思就是你更倾向于相信新的gradient所告诉你的error surface的平滑或陡峭程度,而比较无视于旧的gradient所提供给你的信息。同时随着迭代次数的增加,比较久远的gradient的影响逐步消减,这也更符合常理。
Momentum
通常训练时梯度下降可能卡在local minima、saddle point或plateau的地方,在这三种情况下,对参数的偏微分等于零,或是趋于零而使得训练速度缓慢,可能被误作为最优model而停止训练。
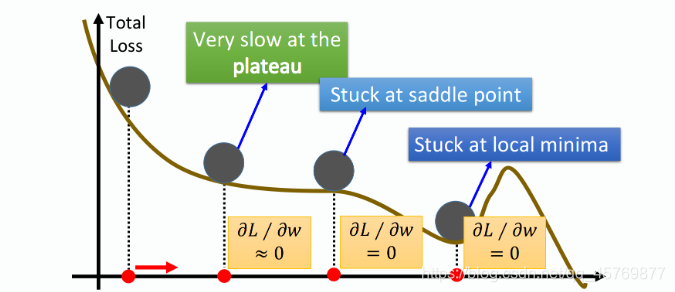 stuck at local minima、saddle point or plateau stuck at local minima、saddle point or plateau
|
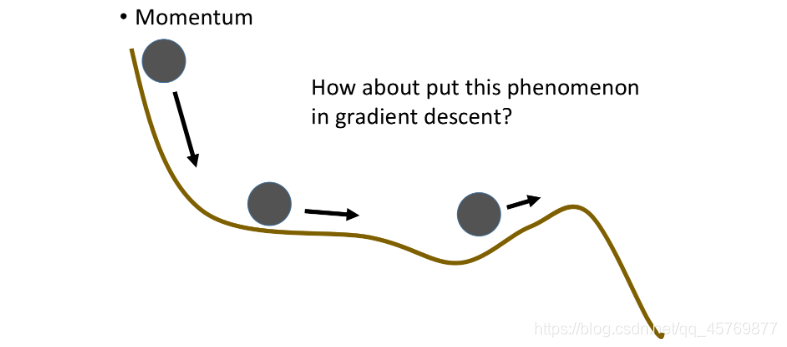 momentum momentum
|
Momentum要做的事就是在梯度下降时,加上一个惯性,使参数能够冲过local minima、saddle point或plateau达到global minima。
update with Momentum
假设每次更新用
m
m
m表示momentum(包括方向和大小)
u
p
d
a
t
e
m
update\ m
update m:
m
t
+
1
=
α
m
t
+
(
1
−
α
)
g
t
m^{t+1}=\alpha m^t+(1-\alpha )g^t
mt+1=αmt+(1−α)gt
u
p
d
a
t
e
θ
update\ \theta
update θ:
θ
t
+
1
=
θ
t
−
η
m
t
+
1
\theta^{t+1}=\theta^t-\eta m^{t+1}
θt+1=θt−ηmt+1
m t + 1 m^{t+1} mt+1的更新同时考虑了前一次更新 v t v^{t} vt,又考虑了参数在当前点的梯度 g t g^t gt, α \alpha α控制了上一次更新对这次更新的影响程度。 m m m的含义既包括上一次更新的方向,又包括上一次更新的距离。
local minima in deep learning
Yann LeCun在07年的时候提出,他说不必太担心local minima的问题,出现local minima的条件是,它必须在每一个dimension都是山谷的低谷形状。假设每个dimension低谷出现的概率为p,由于我们的network有非常非常多的参数,这里假设有1000个参数,local minima出现的几率是 p 1000 p^{1000} p1000,network越复杂,参数越多,这件事发生的概率就越低。
Adam
Adam就是RMSProp+Momentum

Adam algorithm
-
初始化Momentum m 0 = 0 m_0=0 m0=0
-
初始化学习率修正值 v 0 = 0 v_0=0 v0=0
迭代过程:
-
计算gradient g t g_t gt
g t = ∇ θ f t ( θ t − 1 ) g_t=\nabla _{\theta}f_t(\theta_{t-1}) gt=∇θft(θt−1) -
上一次移动的momentum m t − 1 m_{t-1} mt−1和gradient g t g_t gt加权求和得到 m t m_t mt——Momentum
m t = β 1 m t − 1 + ( 1 − β 1 ) g t m_t=\beta_1 m_{t-1}+(1-\beta_1) g_t mt=β1mt−1+(1−β1)gt -
上一次计算的 v t − 1 v_{t-1} vt−1和gradient g t g_t gt的平方加权求和得到的 v t v_t vt——RMSProp
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 v_t=\beta_2 v_{t-1}+(1-\beta_2) g_t^2 vt=β2vt−1+(1−β2)gt2 -
修正初始几步对 m 0 m_0 m0和 v 0 v_0 v0的偏重——Bias Correction
m ^ t = m t 1 − β 1 t v ^ t = v t 1 − β 2 t \hat{m}_t=\frac{m_t}{1-\beta_1^t} \\ \hat{v}_t=\frac{v_t}{1-\beta_2^t} m^t=1−β1tmtv^t=1−β2tvt -
以momentum作为梯度 × × ×RMSProp normalize之后的learnling rate,update参数 θ \theta θ
θ t = θ t − 1 − α v ^ t + ϵ ⋅ m ^ t \theta_t=\theta_{t-1}-\frac{\alpha }{\sqrt{\hat{v}_t}+\epsilon}\cdot \hat{m}_t θt=θt−1−v^t+ϵα⋅m^t
why Bias Correction









 本文详细介绍了AdaGrad、RMSProp、Momentum和Adam算法,探讨了它们在梯度更新中的应用,尤其是Adam算法如何结合RMSProp的动量项和bias correction,以有效避免局部极小值问题。
本文详细介绍了AdaGrad、RMSProp、Momentum和Adam算法,探讨了它们在梯度更新中的应用,尤其是Adam算法如何结合RMSProp的动量项和bias correction,以有效避免局部极小值问题。
















 5210
5210

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








