[学习笔记]冷扩散 Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise

[学习笔记]Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise

原文链接：原文链接

“本作品仅供学习交流使用，严禁用于商业用途。如果保存，请在24小时内删除。作者不承担任何责任。”

标准的扩散模型包括图像变换（添加高斯噪声）和图像恢复算子，该算子逆转这种退化。我们观察到扩散模型的生成行为与图像退化的选择关系不大，事实上可以通过改变这种选择来构建一整个家族的生成模型。即使使用完全确定性的退化（例如模糊、遮罩等），扩散模型的训练和测试时间更新规则也可以很容易地推广到创建生成模型。

从高温（大噪声）状态开始，慢慢冷却到几乎没有噪声的“冷”状态，明确地表明，在扩散模型中，噪声不是必要的，并且去除噪声对许多逆问题有影响。

标准的扩散模型由两个组件组成。首先，存在一个图像退化操作，该操作用高斯噪声污染图像。其次，创建一个经过训练的修复操作来进行去噪。图像生成过程交替应用这两个操作。在本工作中，我们考虑基于任意退化操作构建的一般化扩散。这些退化可以是随机的（如标准扩散的情况）或确定性的。

Model components and training

定义一种操作 $D$ ,使得$x_0$随着$t$连续变化，并且$D(x_0，0)=x_0$。以及我们还需要一个（近似）反转$D$的恢复算子$R$，使得$R(x_t,t)\approx x_0$,在实践中，该算子是通过$\theta$参数化的神经网络来实现的。通过最小化问题训练恢复网络

Sampling from the model

选择退化操作D并训练模型R进行修复后，可以使用这些操作通过从扩散文献中借用的标准方法来反转严重的退化。对于小的退化（t ≈ 0），可以使用一次R来一次获得修复的图像。但是，由于R通常使用简单的凸损失进行训练，因此当t较大时，它会产生模糊的结果。相反，扩散模型过迭代应用去噪操作，然后将噪声重新添加到图像中来进行生成，添加的噪声水平随时间的推移而降低。这对应于算法1中的标准更新序列。

当修复操作完美时，即$R(D(x_0,t),t)=x_0$对于所有$t$，可以很容易地看到算法1产生形式为$x_s=D(x_0,s)$的精确迭代。但是，对于不完美的修复操作会发生什么？在这种情况下，错误可能会导致迭代$x_s$远离$D(x_0,s)$，并且可能无法准确重建。

我们发现算法1中的标准采样方法对于基于噪声的扩散效果良好，可能是因为修复操作R已经训练来纠正（随机高斯）输入中的错误。但是，我们发现它在冷扩散（具有平滑/可微分退化）的情况下效果不佳，如图2所示的去模糊模型所示。我们提出了算法2用于采样，我们发现它对于反转平滑、冷退化更优越。

Properties of Algorithm 2

如果恢复算子$R$是降质算子$D$的完美逆转，那么算法1和2都可以完美地重构。

对于小的$x$和$s$值，算法2对恢复算子$R$中的误差极其宽容。为了理解为什么，考虑一个具有线性降质函数的形式$D(x,s)\approx x+s\cdot e$的问题，其中$e$是一个向量。虽然这个假设可能看起来相当有限，但请注意，任何光滑的降质函数$D(x,s)$在$x=x_0，s=0$附近展开的形式为$D(x,s)\approx x+s\cdot e+HOT$，其中$HOT$表示高阶项。请注意，这个泰勒展开的常数/零阶项是零，因为我们假设降质算子满足$D(x,0)=x$。

对于形式（3.3）和任何恢复算子$R$的退化，可以写入算法2中的更新

通过归纳法，我们看到该算法对于所有$s<t$都产生$x_s=D(x_0,s)$的值，无论$R$的选择如何。换句话说，对于$R$的任何选择，迭代行为都与当$R$是降质算子$D$的完美逆时相同。

相比之下，算法1并没有这种行为。当$R$不是$D$的完美逆转时，$x_0$甚至不是算法1中更新规则的固定点，因为$x_0\ne D(R(x,0),0)=R(x,0)$。如果$R$不能完美地逆向$D$，我们应该期望算法1会引入错误，即使对于小的s值。同时，对于小的s值，D的行为接近其一阶泰勒展开，算法2对R中的误差变得免疫。我们在图2中展示了算法2和算法1的稳定性。

Generalized Diffusions with Various Transformations

Deblurring

我们考虑基于高斯模糊操作（与高斯噪声相反）的广义扩散，其中步骤t处的图像比t−1处的图像具有更多的模糊。因此，给定高斯核{Gs}和步骤t−1的图像xt−1的正向过程可以写成

Inpainting

定义一个变换时间表，该时间表逐渐使输入图像中的像素变灰。我们使用高斯掩模去除像素，我们用$z_{\beta }$表示最终掩模。

Super-Resolution

（没有提到具体的操作）

Snowification

（没有提到具体的操作）

Cold Generation

我们将首先讨论使用高斯噪声的确定性生成，然后详细讨论使用去模糊的无条件生成。最后，我们提供了一个概念证明，即算法2可以扩展到其他退化。

Generation using deterministic noise degradation

我们讨论使用基于噪声的退化的图像生成。我们考虑“确定性”采样，即在生成过程开始时选择并冻结噪声模式，然后将其视为常数。我们研究了在固定噪声的情况下应用算法2的两种方法。定义：
$$D(x,t)=\sqrt{{\alpha }_t}x+\sqrt{1-{\alpha }_t}z$$
在这种情况下，可以通过固定退化算子$D(x,s)$中使用的噪声$z$来应用算法2。或者，可以通过使用以下公式来确定地计算要在重建的步骤t中使用的噪声向量$z$

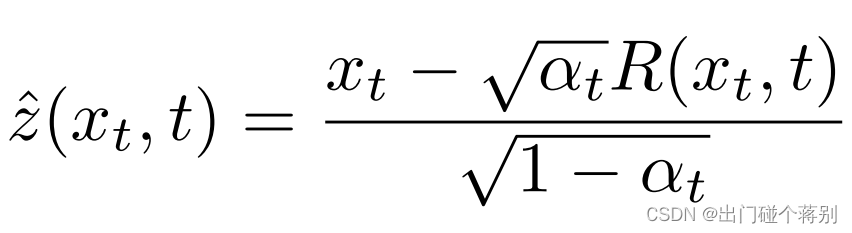
Image generation using blur

当使用模糊作为退化时，完全退化的图像不会形成我们可以从中采样的良好的闭合形式分布。然而，它们确实形成了一个足够简单的分布，可以用简单的方法进行建模。对于大T，每个图像$x_0$退化为恒定的$x_T$（即，每个像素都是相同的颜色）。此外，该常数值正是RGB图像$x_0$的通道平均值，并且可以用3矢量表示。使用高斯混合模型（GMM）可以容易地表示这种三维分布。可以对该GMM进行采样以产生严重模糊图像的随机像素值，可以使用冷扩散对其进行去模糊以创建新图像。

Generation using other transformations

我们将进一步提供生成可以扩展到其他转换的概念证明，人们可能认为一个自然的选择是将所有图像发送到一个完全黑色的图像$x_T$，但这不允许生成任何多样性。因此，我们改为使遮罩将所有像素变成随机的纯色。这仍然从图像中删除了所有信息，但它允许我们从不同颜色的图像开始，通过算法2从学习的分布中恢复不同的样本。
$$x_t=G_t\ast x_0+(1-G_t)\ast c$$
其中c是随机采样的颜色的图像。

此外，为了证明几乎可以反转任何变换，我们包括了一种被称为变形的新变换，即我们迭代地将CelebA的人脸变换为AFHQ的动物脸。尽管我们选择了CelebA和AFHQ进行实验，但原则上，这种插值可以用于任何两个初始数据分布。

Conclusion

现有的扩散模型对于正向和反向过程都依赖于高斯噪声。在这项工作中，我们发现随机噪声可以完全从扩散模型框架中移除，并被任意变换所取代。在此过程中，我们对扩散模型及其采样过程的推广使我们能够恢复受确定性退化影响的图像，例如模糊、修复和下采样。这一框架为超越高斯噪声范式的更多样化的扩散模型铺平了道路。这些扩散的不同性质可能会被证明对一系列应用有用，包括图像生成和其他应用。