（数据结构）图的最小生成树 克鲁斯卡尔算法(Kruskal)

假设要在n个城市之间建立通信联络网，每两个城市之间建立线路都需要花费不同大小的经费，则连通n个城市只需要n-1个条线路，最小生成树解决的问题就是：如何在最节省经费的前提下建立这个通信网
也可以理解为：n个城市之间最多可以建立n(n-1)/2条线路，我们要从这里挑出n-1条线路

实现最小生成树的另一算法：普里姆算法(Prim)

算法思路

克鲁斯卡尔算法(Kruskal)又称加边法，也是采用一种贪心的策略，先将所有边的权值从小到大排序后，然后从小到大依次选择，如果这条边连接的两个顶点v1 v2本来就是不连通的，则添加这条边，如果本来是连通的则不做任何处理，直到所有边都遍历完成。

为了实现算法，我们需要定义一个结构体类型edge

struct edge{
    int from,to;  //边的起始点和终点(对于无向图来说不区分起点和终点)
    int lowcost;  //边上的权值
}edges[maxn];  

同时还需要定义一个辅助数组vexset，vexset[i]表示的是这个顶点所属的连通分量，如果两个顶点的连通分量相同，则说明这两个顶点已经连通。

int vexset[maxn];   //各顶点所属的连通分量（类似并查集）

初始化时需要将每个顶点的连通分量为他自身。

下面上图分析：

1. 这个无向连通图如图所示，并把所有边都加入edges数组
   

2. 对edges数组按照lowcost从小到大排序
   

3. 下面就是一一遍历这10条边

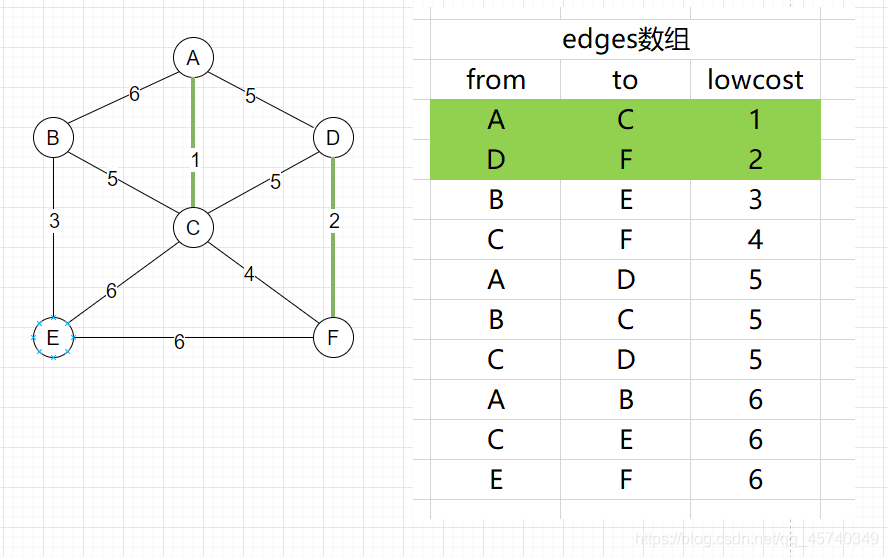
   1. 边AC，由于顶点A和C不连通，所以加入这条边
      

   2. 边DF，由于D和F未连通，所以加入这条边
      

   3. 边BE，由于B和E未连通，所以加入这条边
      

   4. 边CF，由于顶点C和F未连通，所以加入
      

   5. 边AD，由于顶点A和D已经有了一条路径A-C-F-D，再加多一条也是多余的，所以跳过

   6. 边BC，由于B和C未连通，所以加入这条边
      

   7. 现在可以发现所有的顶点都已经相连了，所以剩下的边CD、AB、CE、EF都不会加入到最小生成树里面，所以这个图的最小生成树如下图所示：
      

代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define maxn 1024 //最大的顶点数
//辅助数组Edges，存放的是每一条边上的信息
struct edge{
    int from,to;  //边的起始点和终点(对于无向图来说不区分起点和终点)
    int lowcost;  //边上的权值
}edges[maxn];   
int vexset[maxn];   //各顶点所属的连通分量（类似并查集）
int n,m;  //n为顶点的个数，m为边的个数，其中顶点的编号从1-n
int index = 1;  //用于记录edges数组的当前下标（下标从1开始）

/*
用于对edges排序用的比较函数
*/
bool comp(edge e1,edge e2){
    return e1.lowcost < e2.lowcost;
}

/*
增加一条连接n1 和n2的边，权值为k
*/
void link(int n1,int n2,int k){
    edges[index++] = {n1,n2,k};
}

/*
初始化
*/
void init(){
    //初始化每个顶点的连通分量为他自己
    for(int i = 1;i<=maxn;++i){
        vexset[i] = i;
    }
    n = 6;   //一共有6个顶点
	m = 10;   //10条边
	//下面m行都是在建图
	link(1,2,6);
	link(1,3,1);
	link(1,4,5);
	link(2,3,5);
	link(3,4,5);
	link(2,5,3);
	link(3,5,6);
	link(3,6,4);
	link(4,6,2);
	link(5,6,6);
}


void kruskal(){
    //首先对edges数组，按照边的权值，从小到大排序
    sort(edges + 1,edges + index + 1,comp);
    //从小到大遍历每一条边
	for(int i = 1;i<=index;++i){
		int v1 = edges[i].from;   //这条边连接的两个顶点
		int v2 = edges[i].to;
		int vs1 = vexset[v1];		//两个顶点分别的连通分量
		int vs2 = vexset[v2];
		//如果两个顶点的连通分量相同，则这两个顶点已经是连通的了，不需要加边
		//当两个顶点本来不连通，才需要加边
		if(vs1 != vs2){
			//增加一条边 v1 -- v2
			cout << v1 << " -- " << v2 << endl;
			//合并2个连通分量
			//让所有连通分量为vs1的都改成vs2
			for(int i = 1;i<=n;++i){
				if(vexset[i] == vs1){
					vexset[i] = vs2;
				}
			}
		}
	}
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
	init();
    kruskal();
	return 0;
}

如果有错误，欢迎指正！