题目描述
某教学大楼一层有n个教室,从左到右依次编号为1、2、…、n。现在要把一些课桌从某些教室搬到另外一些教室,每张桌子都是从编号较小的教室搬到编号较大的教室,每一趟,都是从左到右走,搬完一张课桌后,可以继续从当前位置或往右走搬另一张桌子。
输入数据:先输入n、m,然后紧接着m行输入这m张要搬课桌的起始教室和目标教室。
输出数据:最少需要跑几趟。
题意分析
例如有10个教室,有4张桌子要搬
| 起始 | 终点 |
|---|---|
| 1 | 3 |
| 2 | 4 |
| 3 | 9 |
| 4 | 6 |
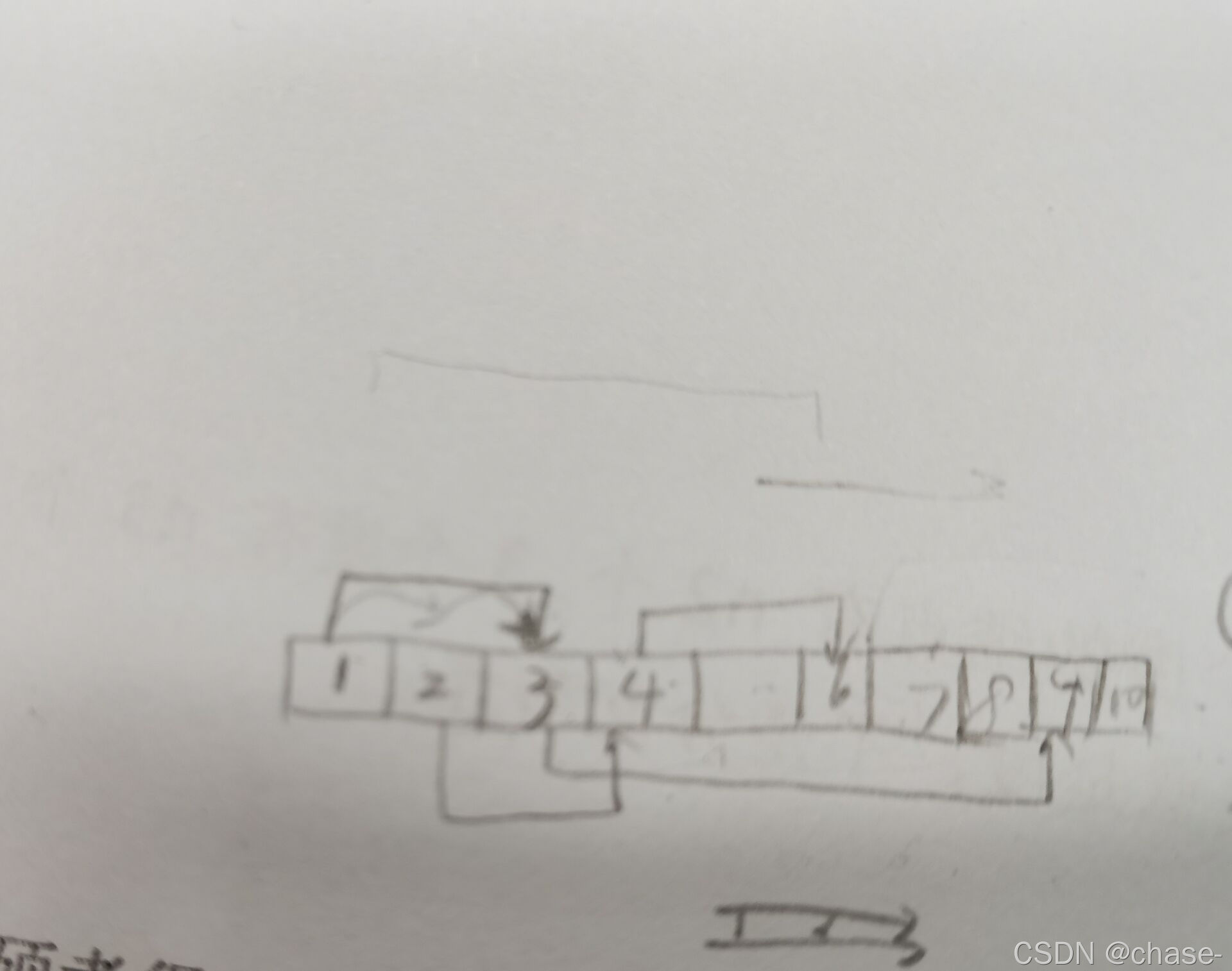
每一趟人只能往右边教室走,当右边没有桌子可以搬的时候算做一趟。
若第一趟搬1->3 3->9, 第二趟2->4, 4->6。则为最少情况,趟数为2
若第一趟1->3 4->6, 第二趟2->4, 第三趟3->9,则不是最少数
故,由题意知每次到某个终点教室选择右边离自己最近教室的桌子去搬即可达到最少次数!
我看了好久这个题,,才知道是啥意思…
代码
用结构体表示桌子,用到了c里面的qsort函数,这个要记一下cmp要怎么改。核心代码看的网上的,自己想得太歪了。
#include<stdio.h>
#include<stdlib.h>
#include<map>
//贪心实现搬桌子,每次搬运离当前桌子最近的桌子
typedef struct desk
{
int start;
int end;
}desk;
// 结构体排序
int cmp(void const* a,void const* b)
{
desk *p=(desk*)a;
desk *q=(desk*)b;
if(p->start!=q->start)
return (p->start)-(q->start);
else
return (p->end)-(q->end);
}
int main()
{
int rooms=0,desks=0;
FILE* fp=fopen("./data.txt","r");
fscanf(fp,"%d %d\n",&rooms,&desks);
// 结构体数组存放desks
desk *dsk = (desk*)malloc(sizeof(desk)*desks);
int *isMove=(int*)malloc(sizeof(int)*desks); //桌子是否搬走
for(int i=0;i<desks;i++)
isMove[i]=0;
for(int i=0;i<desks;i++)
{
fscanf(fp,"%d %d\n",&dsk[i].start,&dsk[i].end);
}
int count=0;//趟数
int tmp=rooms+1;//设置得比任何房间号都大
//设置得比任何房间号都大
qsort(dsk,desks,sizeof(int),cmp);
int pos=dsk[0].start; //当前位置
int num = 0; //已搬桌子数目
while ( num < desks )
{
int temp = 0;
for (int i = 0; i < desks; ++i )
{
// 从左到右
if (temp <= dsk[i].start && isMove[i]!=1)
{
// 下一个位置
temp = dsk[i].end;
isMove[i] = 1;
num++;
}
}
count++;
}
printf("%d",count);
getchar();
}
输入

输出









 本文解析了一道关于在教学大楼中根据特定规则搬动课桌以最小化趟数的问题。通过理解题目描述的贪心策略,如何从左到右优先选择右侧最近的空教室,展示了代码实现和解题思路。
本文解析了一道关于在教学大楼中根据特定规则搬动课桌以最小化趟数的问题。通过理解题目描述的贪心策略,如何从左到右优先选择右侧最近的空教室,展示了代码实现和解题思路。
















 544
544

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








