汉诺塔问题

汉诺塔问题，是心理学实验研究常用的任务之一。该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘，三根柱子分别为起始柱A、辅助柱B及目标柱C。

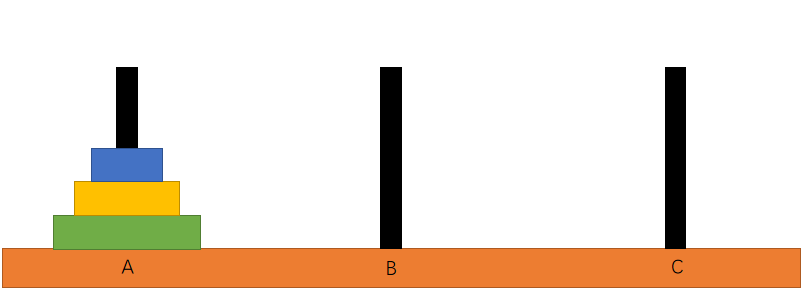
操作规则：每次只能移动一个盘子，并且在移动过程中三根柱上都始终保持大盘在下，小盘在上、操作过程中盘子可以置于A、B、C任一杆上。

解题步骤：（分为两步）

第一步：

​ 把 n-1 个圆盘 从 柱1 移动到 柱2；

​ 把第 n 个圆盘 从 柱1 移动到 柱3；

第二步：

​ 把 n-1 个圆盘从 柱2 移动到 柱3 ；

原理

要解决 n 层的汉诺塔

必须解决 n-1 层的汉诺塔

…

必须解决 1 层的汉诺塔（塔1 – > 塔3）

代码实现：

#include <stdio.h>

void hanoi(int n, char a, char b, char c)
{
	if (n == 1)
	{
		printf("从柱%c 移动到 柱%c\n", a, c);
	}
	else
	{
		hanoi(n - 1, a, c, b);
		printf("从柱%c 移动到 柱%c\n", a, c);
		hanoi(n - 1, b, a, c);
	}
}
int main()
{
	hanoi(2, 'A', 'B', 'C');
	return 0;
}

运行效果图：

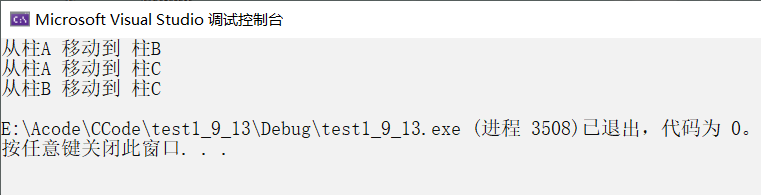
希望可以对大家有所帮助，如果有什么不对的地方，还烦请指教，谢谢！