【数据结构】散列表（hash）的查找技术

• 散列函数的构造
  直接定址法
  除留余数法
  数字分析法
  平方取中法
  折叠法（分段叠加法）
• 冲突处理方法
  开放定址法
  链地址法
  建立公共溢出区

散列的基本思想：在记录的存储地址和它的关键码之间建立一个确定的对应关系。这样，不经过比较，一次读取就能得到所查元素的查找方法。

基本概念

1.散列表：采用散列技术将记录存储在一块连续的存储空间中，这块连续的存储空间称为散列表。
2.散列函数：将关键码映射为散列表中适当存储位置的函数。
3.散列地址：由散列函数所得的存储位置址 。
4.冲突：对于两个不同关键码ki≠kj，有H(ki)＝H(kj)，即两个不同的记录需要存放在同一个存储位置,ki和kj相对于H称做同义词。

• 散列既是一种查找技术，也是一种存储技术。

• 散列只是通过记录的关键码定位该记录，没有完整地表达记录之间的逻辑关系，所以，散列主要是面向查找的存储结构。

• 散列技术一般不适用于允许多个记录有同样关键码的情况。
  有冲突，降低了查找效率，体现不出计算式查找的优点

• 散列方法也不适用于范围查找
  不能查找最大值、最小值
  也不可能找到在某一范围内的记录。

散列技术的关键问题：
⑴ 散列函数的设计。如何设计一个简单、均匀、存储利用率高的散列函数。
⑵ 冲突的处理。如何采取合适的处理冲突方法来解决冲突。

散列函数的设计

直接定址法

散列函数是关键码的线性函数，即：H(key) = a* key + b （a，b为常数）
事先知道关键码，关键码集合不是很大且连续性较好。

除留余数法

H(key)=key mod p
一般情况下，选p为小于或等于表长（最好接近表长）的最小素数

数字分析法

根据关键码在各个位上的分布情况，选取分布比较均匀的若干位组成散列地址。

平方取中法

对关键码平方后，按散列表大小，取中间的若干位作为散列地址（平方后截取）。

折叠法

将关键码从左到右分割成位数相等的几部分，将这几部分叠加求和，取后几位作为散列地址。

冲突的处理

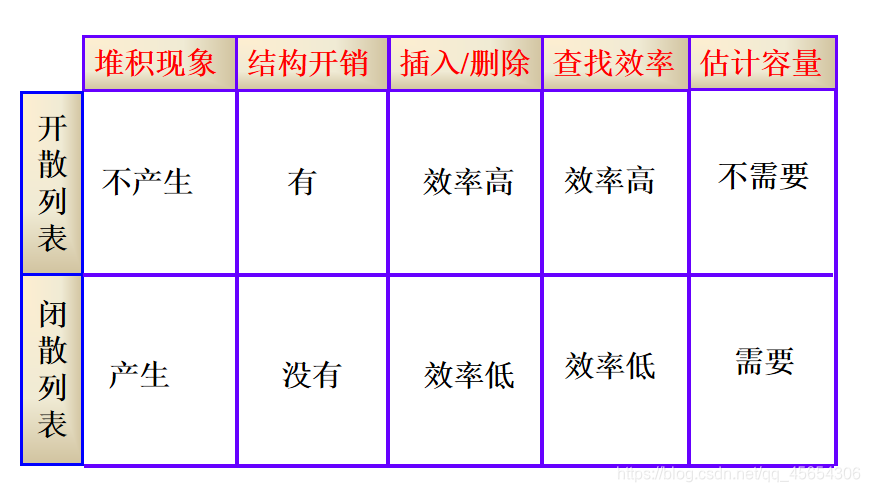
开散列方法( open hashing，也称为拉链法，separate chaining ，链地址法)

闭散列方法( closed hashing，也称为开地址方法，open addressing ，开放定址法)

建立公共溢出区

开放地址法

由关键码得到的散列地址一旦产生了冲突，就去寻找下一个空的散列地址，并将记录存入。
寻找下一个空的散列地址
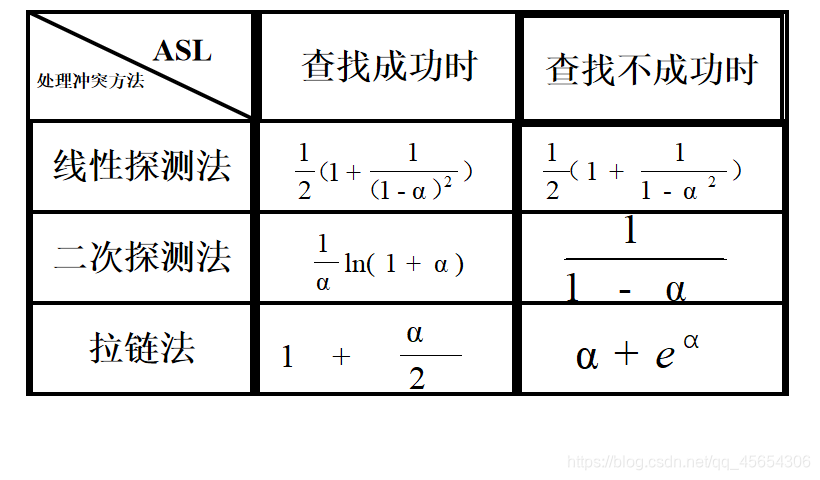
（1）线性探测法
（2）二次探测法
（3）随机探测法
（4）再hash法

线性探测法

当发生冲突时，从冲突位置的下一个位置起，依次寻找空的散列地址。
对于键值key，设H(key)=d，闭散列表的长度为m，则发生冲突时，寻找下一个散列地址的公式为：
Hi=(H(key)＋di) % m （di=1，2，…，m-1）

二次探测法

当发生冲突时，寻找下一个散列地址的公式为：
Hi=(H(key)＋di)% m
（di=12，－12，22，－22，…，q2，－q2且q≤m/2）

随机探测法

当发生冲突时，下一个散列地址的位移量是一个随机数列，即寻找下一个散列地址的公式为：
Hi=(H(key)+di)% m
（di是一个随机数列，i=1，2，……，m-1）

拉链法（链地址法）

基本思想：将所有散列地址相同的记录，即所有同义词的记录存储在一个单链表中（称为同义词子表），在散列表中存储的是所有同义词子表的头指针。
用拉链法处理冲突构造的散列表叫做开散列表。
设n个记录存储在长度为m的散列表中，则同义词子表的平均长度为n / m。