切割【蓝桥杯2019国赛】

嵩韵儿

于 2021-06-06 18:37:59 发布

阅读量1.3k

点赞数 8

CC 4.0 BY-SA版权

分类专栏：蓝桥杯

本文链接：https://blog.youkuaiyun.com/qq_45181299/article/details/117633832

蓝桥杯专栏收录该内容

11 篇文章

订阅专栏

该博客讨论了在4x4的方格矩阵中，直线可能穿过的方格集合的不同情况。通过分析，得出直线可以穿过0到7个方格，并考虑了0个方格的特殊情况，总共有 pow(2,8)-1+12 种不同的集合可能。文章以代码形式展示了计算过程。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

测题链接

在 4 × 4 的方格矩阵中画一条直线。则直线穿过的方格集合有多少种不同的可能？

这个里直线穿过一个方格当且仅当直线将该方格分割成面积都大于 0 的两部分。

~~简单不简单----咱也不敢说，咱也不敢问~~~ 反正是容易漏算~

题意：问直线穿过方格的集合有多少种。

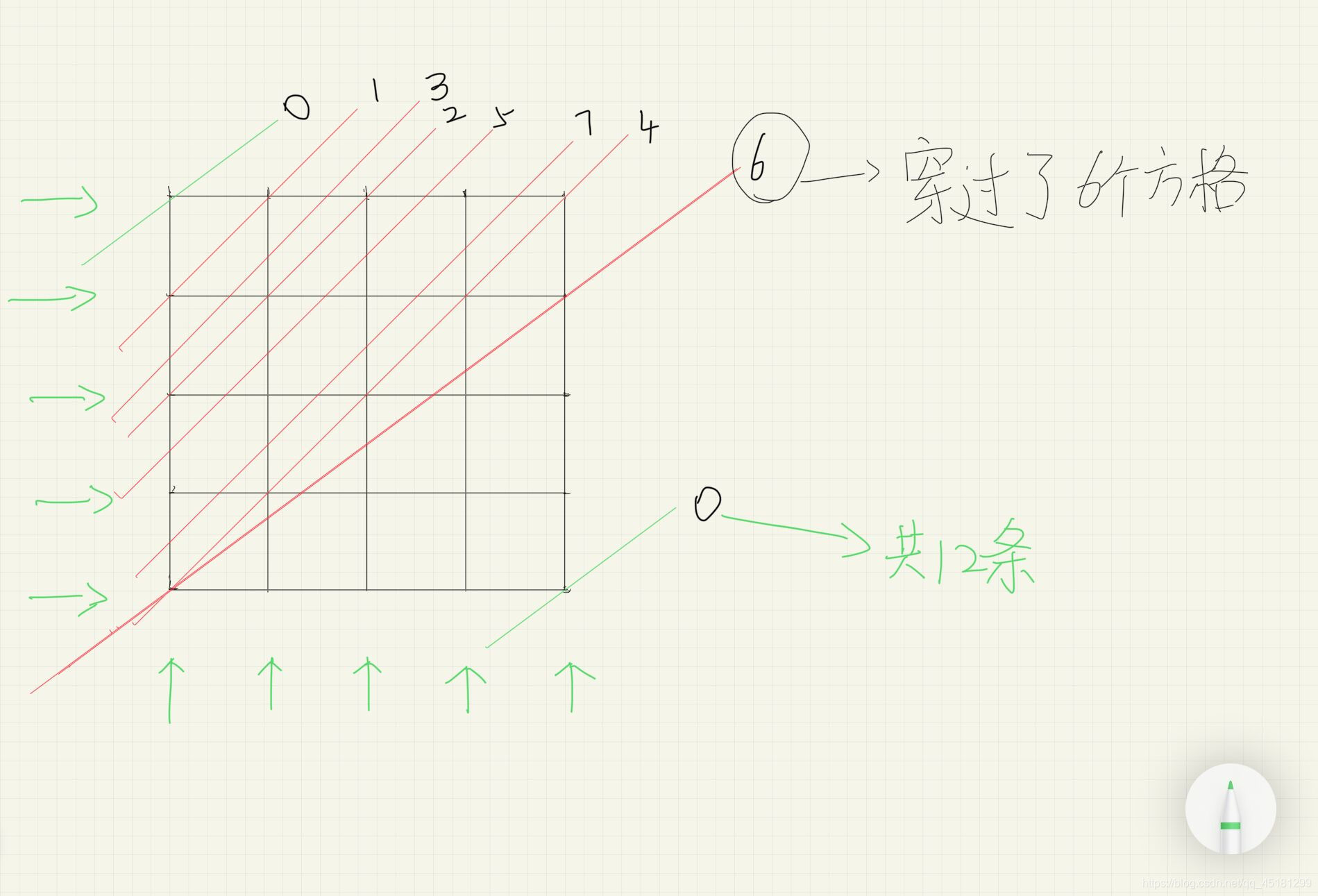
分析：如下草图，大概辅助理解一下..

1、首先可以看出直线穿过方格共有8种可能（可以穿过0、1 、2 、3 、4 、5 、6 、7 个方格）所以这8种可能构成的集合的子集有 $2^8$ 种，但是空集排除，所以就是 $2^8-1$ 种情况；

2、再来.... 若集合只有穿过0个方格的元素，有12种情况，第一条算出的子集包含一种，所以+11 就可以啦~

完~

Code：

#include<bits/stdc++.h>
using namespace std;
int main()
{
  cout<<pow(2,8)-1+12<<endl;
///集合   0-1-2-3-4-5-6-7      组合数就是pow(2,8)-1 （不能有空集）  因为0的直线有12种  横5+竖5 +对角线 2..   
  return 0;
}