正则化

正则化的目的是控制模型的学习容量,减弱过拟合的风险。不论是参数化的线性模型，神经网络和卷积神经网络等，还是无参数的决策树以及朴素贝叶斯等，机器学习模型均存在过拟合现象。过拟合的外在表现是：模型在训练集上的准确率明显高于在测试集上的准确率，即模型对训练集学的比较好，对测试集学的比较差。所以在实践中，经常利用这个性质来判断模型是否发生过拟合，如果过拟合，就需要加强正则化强度。
.
有一句话说的过拟合，我觉得挺好的，“一个过配的模型试图连误差(噪音)都去解释(而实际上噪音是不需要解释的)导致泛化能力比较差，显然就过犹不及了”

1.范数正则化(适用于参数化模型)

1.1 L2正则化（最常用）

L2正则化，即在损失函数(越小越好)中增加权重w的平方和 ∑1/2 λw²，正常数λ是正则化系数，λ越大说明正则化强度越大。
α是权重w对损失函数的敏感程度，α越大，表示权重对损失的影响越大，权重越重要。对式子求导，使dloss/dw=0,得出w=1/(1+入/w)*w0，表明重要的权重受正则化影响小，不重要的权重受正则化影响大，其值会趋近于0，但不等于0。

reg=10**(-4)
regloss=0.5*reg*np.sum(w*w)

1.2 L1正则化

L2正则化，即在损失函数中增加权重w的绝对值和 ∑λ|w|，正常数λ是正则化系数，λ越大说明正则化强度越大。
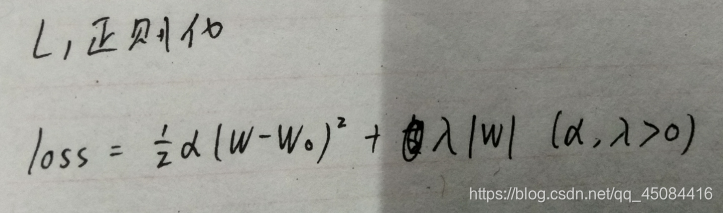因为|w|在w=0处不可导，所以可以假设w0>0，得最优权重w=max(w0-入/α,0)，分析这个式子，重要的权重(α大的)会趋近于0，不重要的权重(α小的)会等于0。将w0<0的话，会得到同样的结论。

1.3 L0正则化

L0正则化，主要目的是使权重尽可能为0，使权重变得稀疏。但由于它不可导，所以实践中几乎不采用。而且L1正则化也有稀疏特性，所以常采用L1代替L0。