计数排序

4.计数排序

概念：1）找出待排序的数组中最大和最小的元素，（2）统计数组中每个值为i的元素出现的次数，存入数组C的第i项

，（3）对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加），（4）反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1。

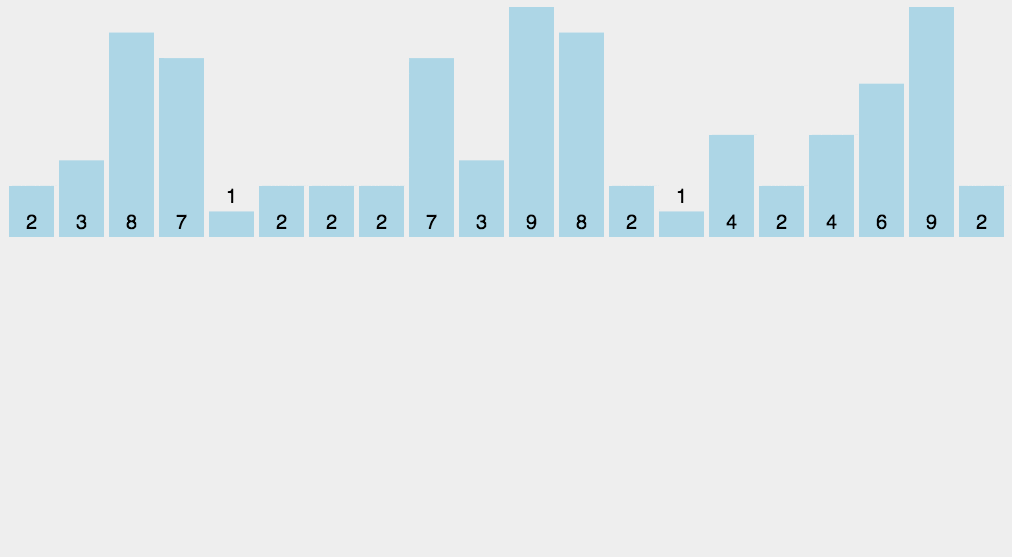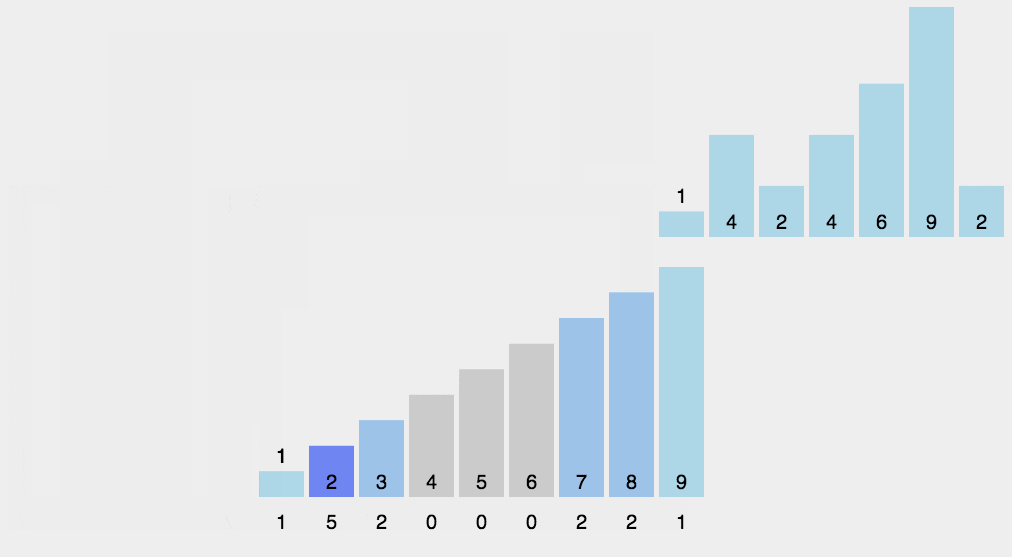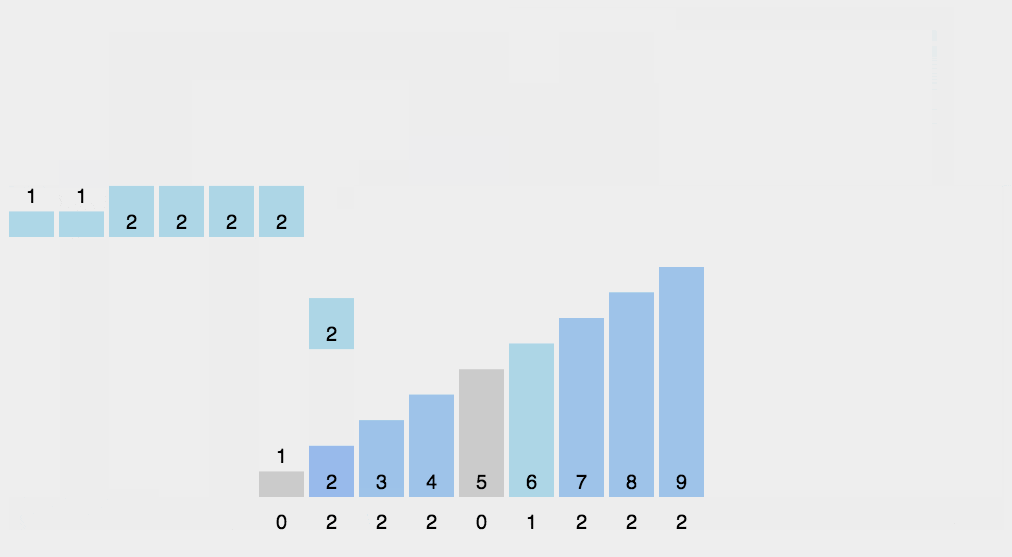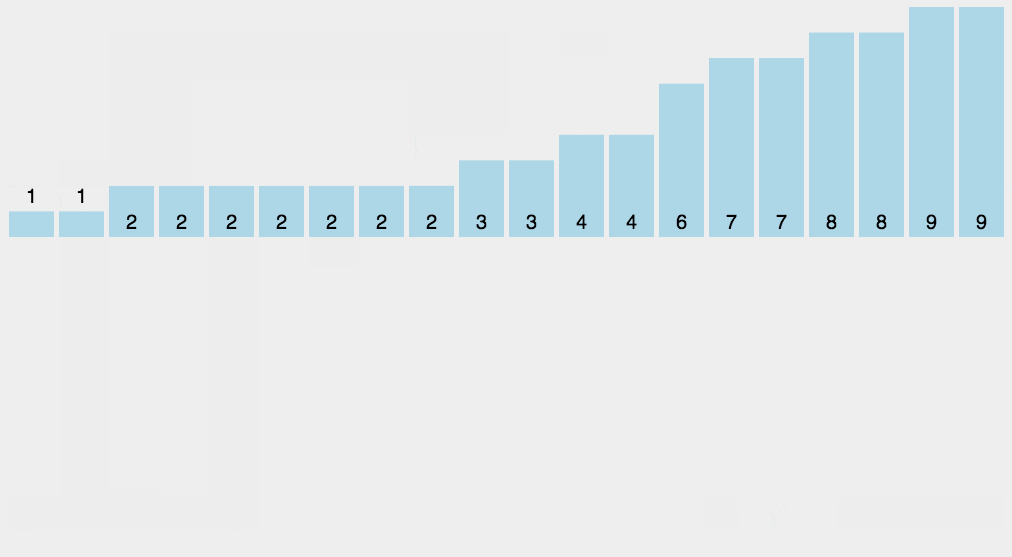
  public static void countSort(){
        int[] arr={8,5,9,2,7,4,6,1,3,10,-3,-2,-10};
        int min=arr[0];
        int max=arr[0];
        for(int i=0;i<arr.length;i++){//O(n)
            if(arr[i]>max){
                max=arr[i];
            }
            if(arr[i]<min){
                min=arr[i];
            }
        }
        int[] nums=new int[max-min+1];
        int offset=min;
        for(int i=0;i<arr.length;i++){//O(n)
            nums[arr[i]-offset]++;
        }
        int index=0;
        for(int i=0;i<nums.length;i++){//O(m)
            if(nums[i]!=0){
                for(int j=0;j<nums[i];j++){
                    arr[index++]=i+offset;
                }
            }
        }
        show(arr);//show方法输出展示
    }

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 Θ(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。

由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。