[LeetCode] 46.全排列

全排列

描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。
你可以 按任意顺序 返回答案。

样例

输入：nums = [1,2,3]
输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

原题链接

思路

枚举所有可能的结果，判断当前节点是否符合判定条件，一旦不符合，就退回上一个节点，重新选择，再继续向下判定搜索。

从数组中选择1个数，作为搜索起点，在剩下的还没被选择的元素中，依次选择一个数，进行组合，直到一个排序序列中的数已经够了。

出口：当序列长度==数组长度时

例如：选择1作为起点开始搜索，依次选择了2和3进行组合，成功组成一条合法路径。（元素一旦被选中，在接下来的选择中，就不能再出现了。因此需要修改状态，对其进行标记，以免被重复选择。）

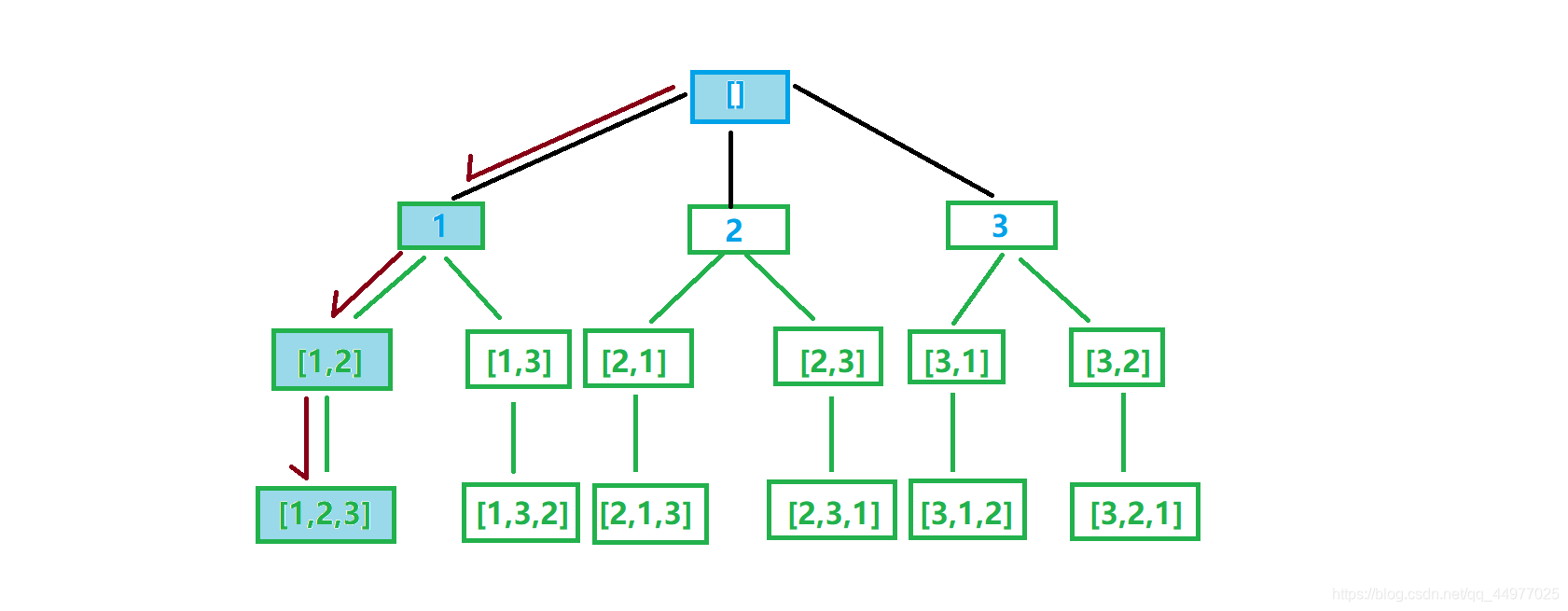
得出1条结果后，撤销当前选择，向上返回，重新选择搜索起点
（因为被选中了，在之后的选择中就不能再使用了，现在我们要换一条路走，就应该赦免它们了，因此需要撤销选择，这样返回上一个节点后才能被重新选择。）

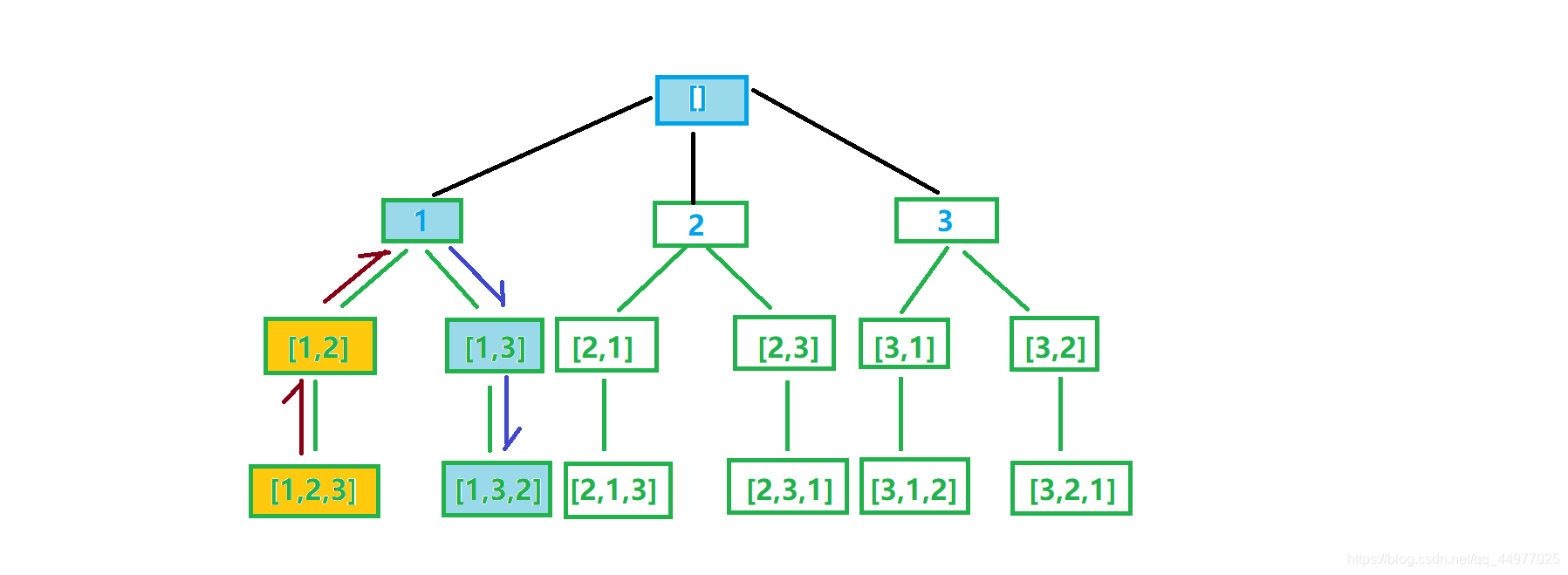
依次类推，按顺序枚举每一条可能的路径，组合成所有的全排列结果。

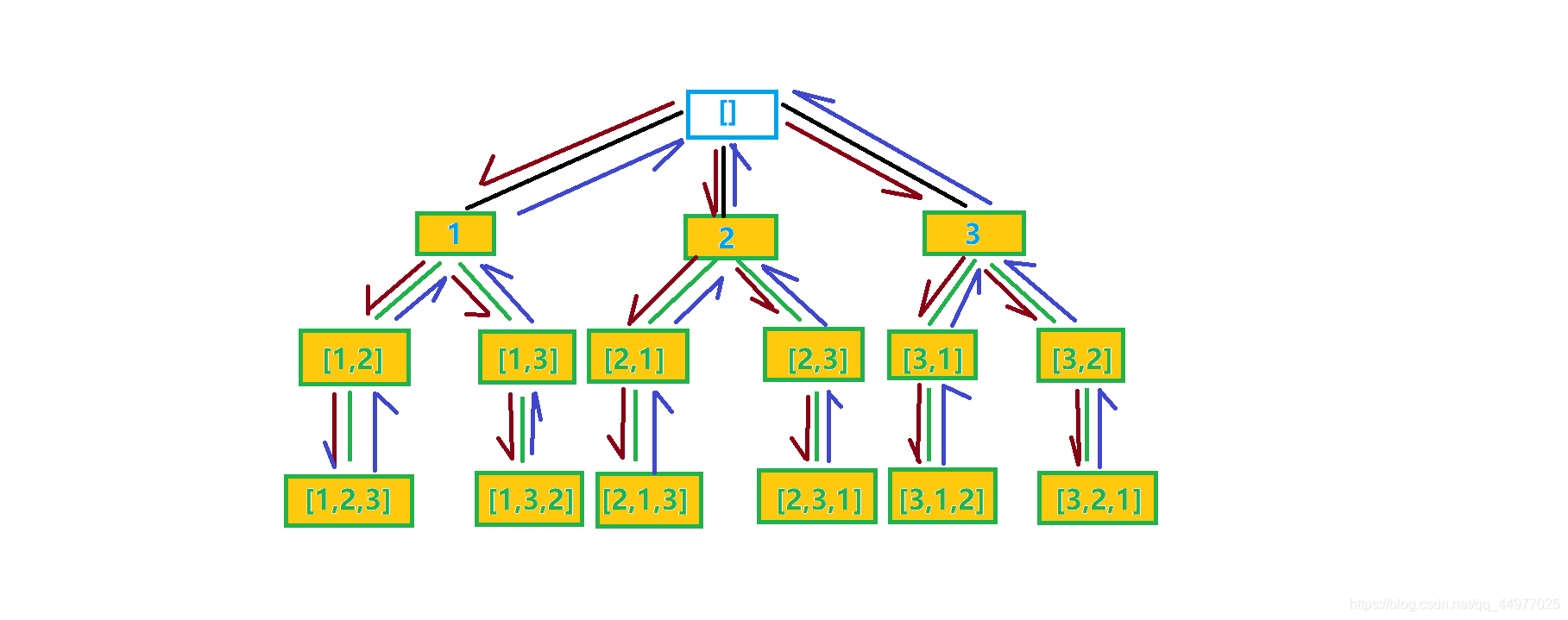
代码

public class Main {
    public static List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> res=new ArrayList<>();
        if (nums==null || nums.length==0){
            return res;
        }
        int len=nums.length;
        //存储每一条合法路径
        Deque<Integer> path=new LinkedList<>();
        //标记走过的位置
        boolean[] used=new boolean[len];
        dfs(nums,len,0,path,used,res);
        return res;
    }

    private static void dfs(int[] nums,int len, int depth, Deque<Integer> path,
                            boolean[] used, List<List<Integer>> res) {
        if(depth>nums.length){
            return;
        }
        //出口：当合法路径的长度==数组长度，即可退出
        if(depth==len){
            res.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < len; i++) {
            //走过的就跳过
            if (used[i]){
                continue;
            }
            //进行选择
            path.addLast(nums[i]);
            used[i]=true;
            dfs(nums,len,depth+1,path,used,res);
            //撤销选择，回到上一层节点，重新选择
            path.removeLast();
            used[i]=false;
        }
    }
}

极力推荐这篇题解：
专业详细题解

上述如有理解有误或表述不当的地方，还请批评指正，谢谢！