KNN算法笔记

KNN原理

KNN的原理是计算要预测的数据点和每个已知数据之间的距离，将距离排序，然后选定一个合适的K值，即从所有距离中找到离预测点最近的K个距离对应的数据，这K个点都有对应的类别，对比这K个样本的类别，让预测点归类为K个最邻近样本中最多数的类别。
KNN算法采用测量不同特征值之间的距离方法进行分类。

决策规则

分类决策规则
一般使用多数表决法（少数服从多数），从而确定预测点的类别。
回归决策规则
常采用均值回归，经验风险最小化。

距离度量

当p=1时，就是曼哈顿距离(对应L1范数)
曼哈顿距离对应L1-范数，也就是在欧几里得空间的固定直角坐标系上两点所形成的线段对轴产生的投影的距离总和。例如在平面上，坐标（x1, y1）的点P1与坐标（x2, y2）的点P2的曼哈顿距离为：|x1−x2|+|y1−y2||x1−x2|+|y1−y2|，要注意的是，曼哈顿距离依赖座标系统的转度，而非系统在座标轴上的平移或映射。

当p=2时，就是欧氏距离（对应L2范数）
最常见的两点之间或多点之间的距离表示法，又称之为欧几里得度量，它定义于欧几里得空间中。n维空间中两个点x1(x11,x12,…,x1n)与 x2(x21,x22,…,x2n)间的欧氏距离 。

k值选择

1、如果选择较小的K值，就相当于用较小的邻域中的训练实例进行预测，学习的近似误差会减小，只有与输入实例较近的训练实例才会对预测结果起作用，单缺点是学习的估计误差会增大。
K值减小就意味着整体模型变复杂，分的不清楚，就容易发生过拟合。过拟合：一个假设在训练数据上能够获得比其他假设更好的拟合。
2、如果选择较大K值，就相当于用较大邻域中的训练实例进行预测，其优点是可以减少学习的估计误差，但近似误差会增大，也就是对输入实例预测不准确，K值增大就意味着整体模型变的简单。
近似误差：可以理解为对现有训练集的训练误差。
估计误差：可以理解为对测试集的测试测试机误差。估计误差小，说明对测试集它的预测效果更好。
选择流程：
1） 计算已知类别数据集中的点与当前点之间的距离
2） 按距离递增次序排序
3） 选取与当前点距离最小的k个点
4） 统计前k个点所在的类别出现的频率
5） 返回前k个点出现频率最高的类别作为当前点的预测分类

算法优缺点

优点：简单；易于理解；容易实现；通过选择K可具备丢噪音数据的健壮性。
缺点：需要大量空间存储已知数据；复杂度高；样本分布不均匀时，未知数据容易归类错误。

KD树

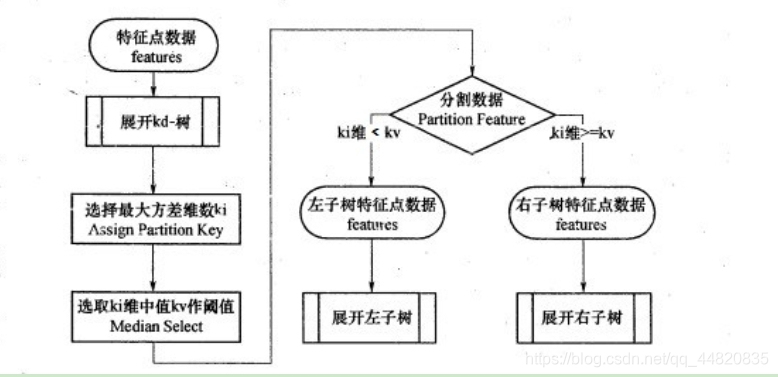
所谓的KD树就是K个特征维度的树，对K维空间中的样本点进行存储以便对其进行快速检索的树形数据结构。KNN中的K代表最近的K个样本，KD树中的K代表样本特征的维数n。
利用KD树可以省去对大部分数据点的搜索， 从而减少搜索的计算量。
KD树算法包括建树，搜索最近邻，预测。
KD树建树采用的是从m个样本的n维特征中，分别计算n个特征的取值的方差，用方差最大的第k维特征nk来作为根节点。对于这个特征，我们选择特征nk的取值的中位数nkv对应的样本作为划分点，对于所有第k维特征的取值小于nkv的样本，我们划入左子树，对于第k维特征的取值大于等于nkv的样本，我们划入右子树，对于左子树和右子树，我们采用和刚才同样的办法来找方差最大的特征来做更节点，递归的生成KD树。