python：关于sum（）函数中axis的一些理解（tensor，ndarray）

最新推荐文章于 2024-06-13 14:53:48 发布

皮_仔

最新推荐文章于 2024-06-13 14:53:48 发布

阅读量1k

点赞数 9

文章标签： python numpy 机器学习

本文链接：https://blog.youkuaiyun.com/qq_44673524/article/details/132971447

版权

前言

在学习sum函数的过程中，经常把求和的维度弄混。每次使用都需要一段时间来梳理用法。最近对sum函数中的“axis=”参数有了更好的理解。为防止忘记，写一篇帖子记录，也希望能对看到的人有所帮助。

注意：所用语言为python，针对的对象是tensor，ndarray中的axis参数。

正文

数组

以一个ndarray类型的3维数组举例：

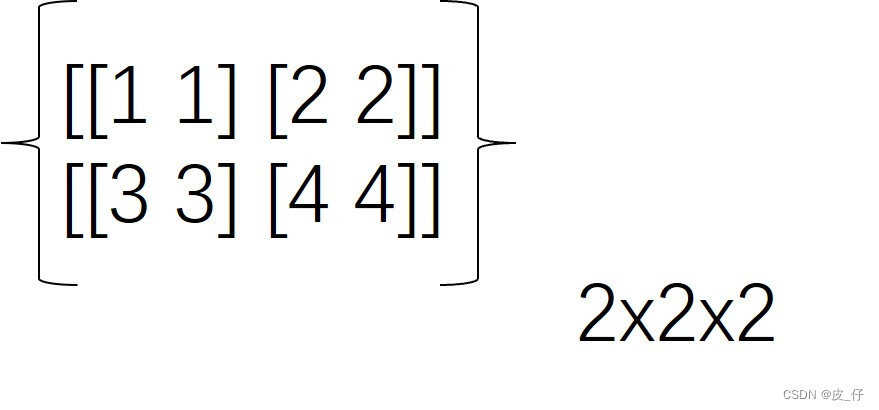
该数组的形状为 (2,2,2) 。

需要理解的是，这是一个3维数组，也就是说axis的取值在 [0,1,2] 内，当axis=0代表最左端的维度，记为第0维，这个维度有两个对象；axis=1是中间维度，记为第1维，维度内也有两个对象；axis=2是中间维度，记为第2维，维度有两个对象。

借助下方的树状图，可以更好的理解维度，还有维度内的对象个数。

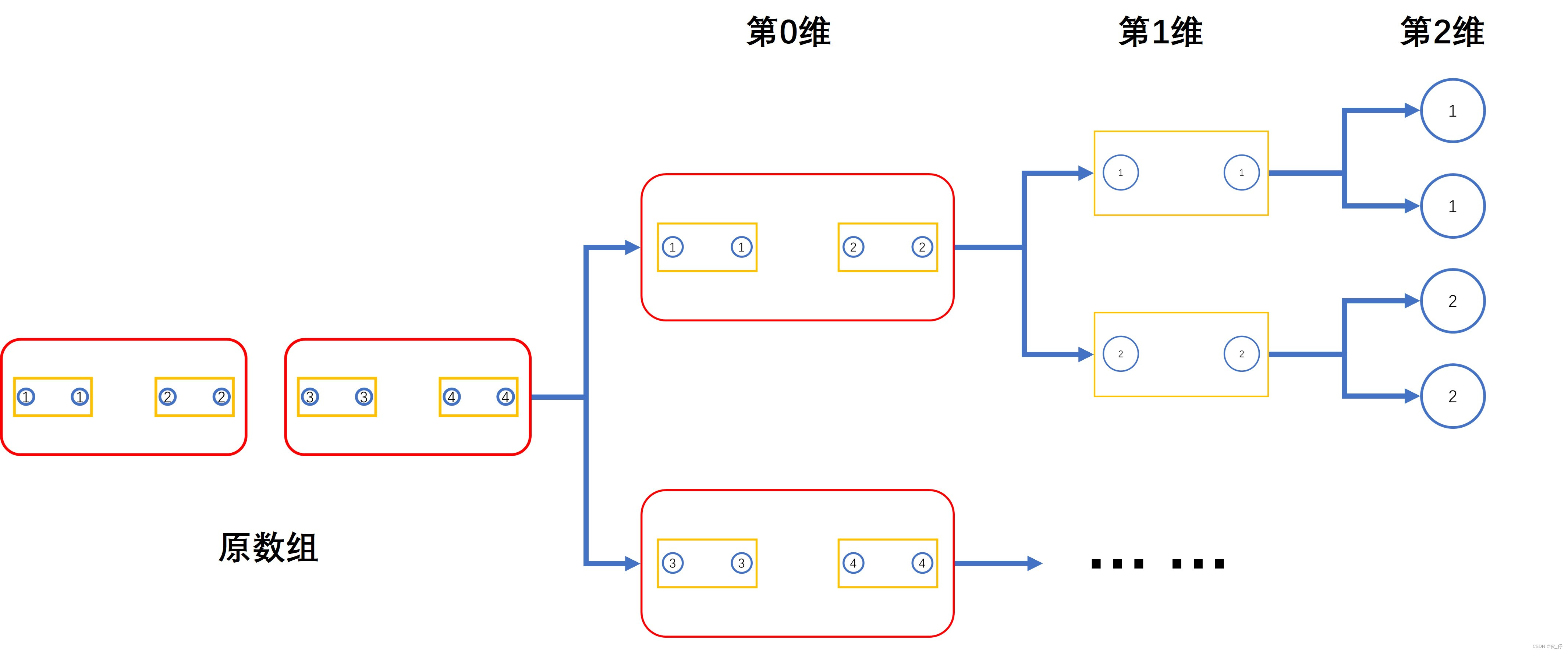
注意：不同的外框形状，代表不同的数组维度。

计算

这是python中np.sum()函数的参数。

def sum(a, axis=None, dtype=None, out=None, keepdims=np._NoValue,
        initial=np._NoValue, where=np._NoValue):

axis表示按维度（轴）求和，默认是第None，即全部元素相加，得到一个数。

dtype表示数据格式，如int，float。

keepdims，即是否保持原先的维度。

假设axis=None，全部元素求和。

求得：20

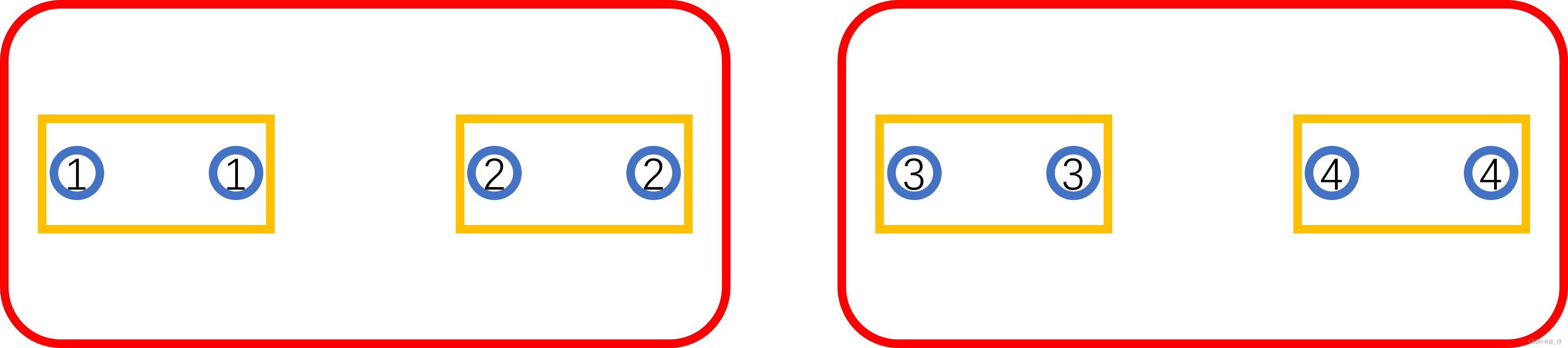
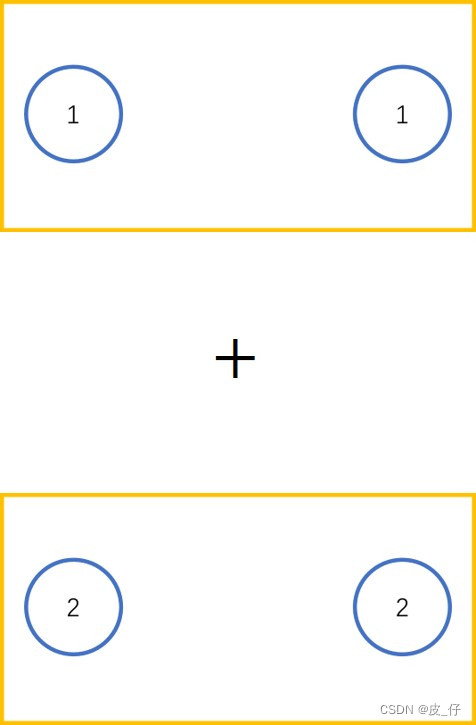
假设axis=0，说明第0维的元素（圆角矩形）全部相加。

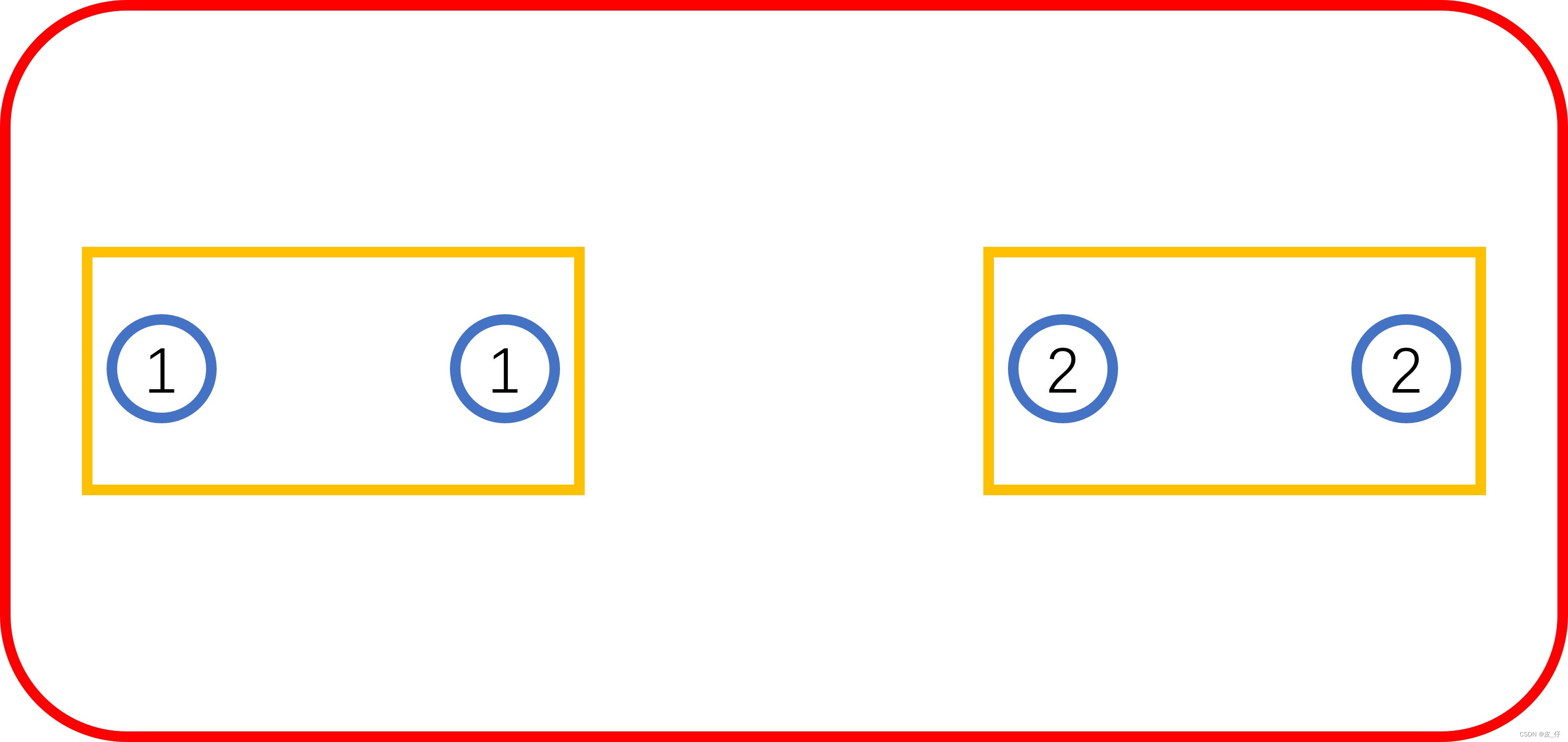
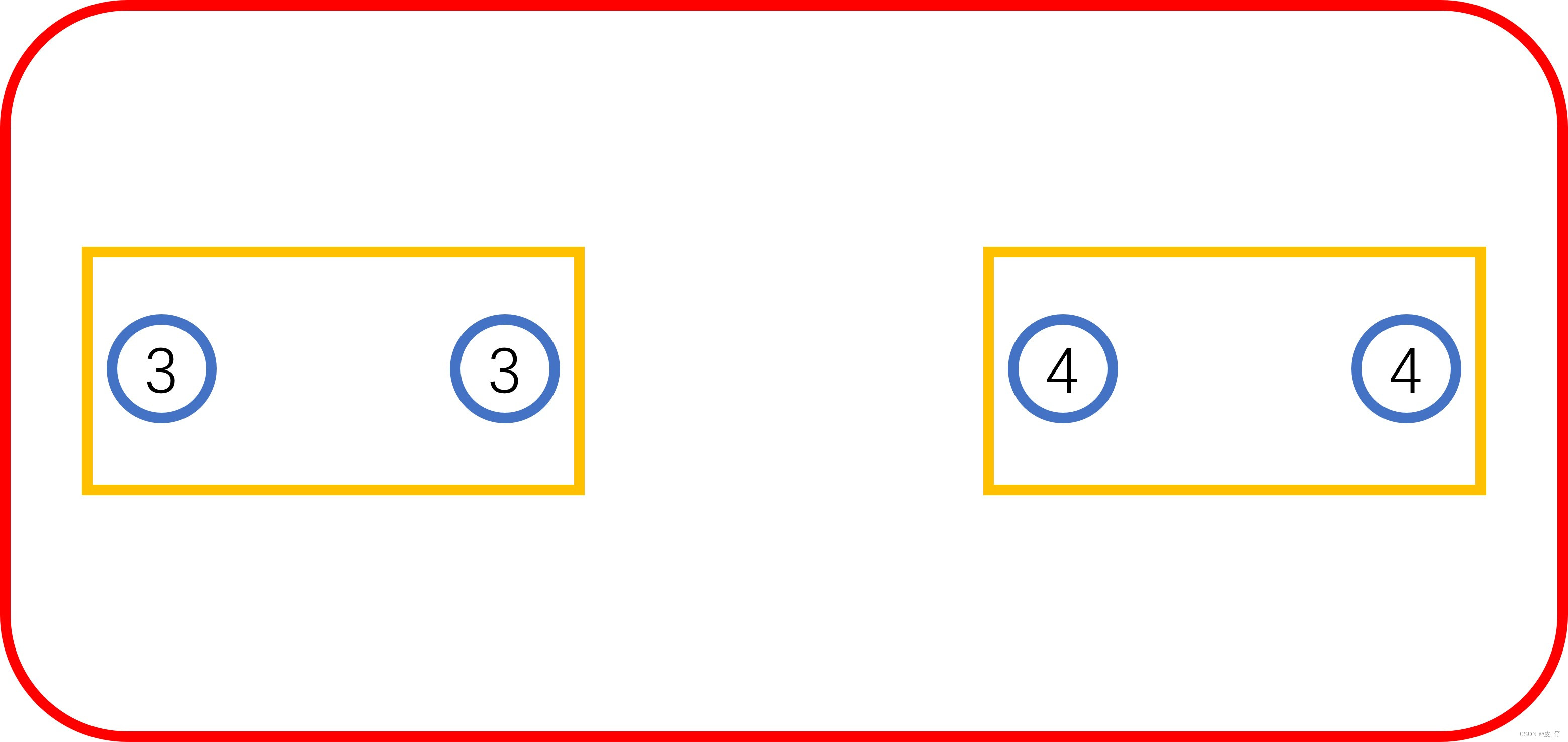
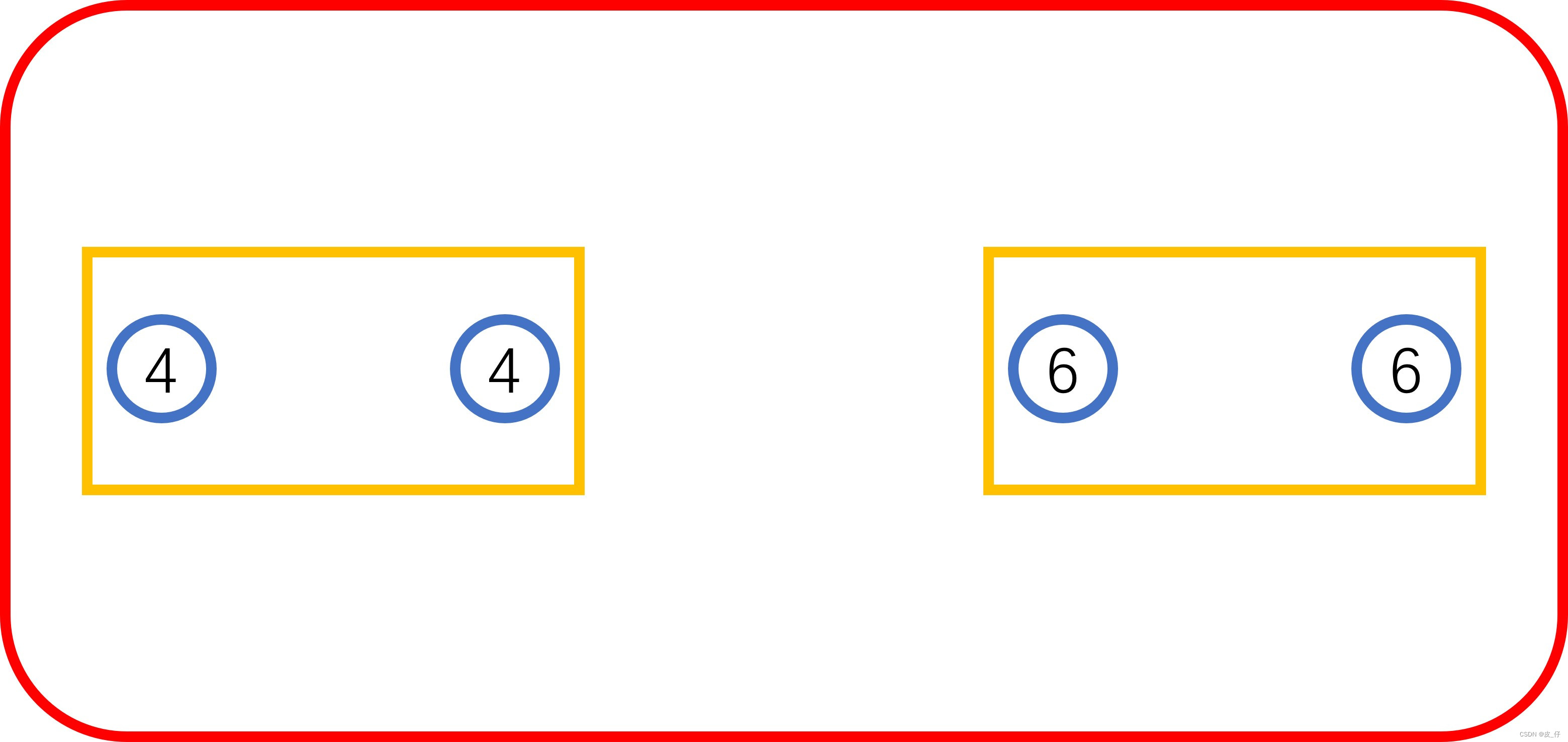
求得： [[4, 4], [6, 6]]，形状为（2，2）。

如果保持维度keepdims=True，即[ [[4, 4], [6, 6]] ]，形状为（1，2，2）

同理，再假设axis=1，说明第1维的元素（矩形）全部相加。同时第0、2维保持不变，即不能越过圆角矩形的范围求和，也不能把矩形内的2个圆变成1个。

求得：[[3,3]，[7,7]]，形状为（2,2）。

如果保持维度keepdims=True，即[ [[3,3]]，[[7,7]] ]，形状为（2,1,2）

验证

在python中进行验证

import numpy as np  # 导入numpy

array = np.array([[[1, 1], [2, 2]], [[3, 3], [4, 4]]])  # 构建数组array

sum_total = array.sum()  # 全部元素求和
sum_0 = array.sum(axis=0)  # 第 0 维求和
sum_0_k = array.sum(axis=0, keepdims=True)  # 第 0 维求和,保持维度
sum_1 = array.sum(axis=1)  # 第 1 维求和
sum_1_k = array.sum(axis=1, keepdims=True)  # 第 1 维求和,保持维度
sum_2 = array.sum(axis=2)  # 第 2 维求和
sum_2_k = array.sum(axis=2, keepdims=True)  # 第 2 维求和,保持维度

print(f"全部元素求和:{sum_total}")
print(f"第 0 维求和:{sum_0},形状:{sum_0.shape}", f"保持维度:{sum_0_k},形状:{sum_0_k.shape}", sep="\n")
print(f"第 1 维求和:{sum_1},形状:{sum_1.shape}", f"保持维度:{sum_1_k},形状:{sum_1_k.shape}", sep="\n")
print(f"第 2 维求和:{sum_2},形状:{sum_2.shape}", f"保持维度:{sum_2_k},形状:{sum_2_k.shape}", sep="\n")

结果