非参数回归

一元非参数回归

给定一组样本观测值$(Y_1,X_1),(Y_2,X_2),\cdots ,(Y_n,X_n),$$X_i$和$Y_i$之间的任意函数模型表示为
$$Y_i=m(X_i)+{\epsilon }_i,i=1,2,\cdots ,n.$$
其中$m(\cdot )=E(Y|X),\epsilon$为随机误差项,一般假定$E(\epsilon |X=x)=0$,$\mathrm{v}\mathrm{a}\mathrm{r}(\epsilon |\mathrm{X}=\mathrm{x})={\sigma }^2$,不必是常数。

核回归光滑模型

参考上篇文章讲到的核密度估计法,相当于求$x$附件的平均点数,平均点数的求法是对可能影响到$x$的样本点,按照距离$x$的远近作距离加权平均.核回归光滑的基本思路之类似，在此不是求平均点数,而是估计点$x$处$y$的取值,仍然按照距离$x$的远近对样本观测值$y_i$加权,这一思想被称为$\mathrm{N}\mathrm{a}\mathrm{d}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{y}\mathrm{a}-\mathrm{W}\mathrm{a}\mathrm{t}\mathrm{s}\mathrm{o}\mathrm{n}$核回归.

• 选择核函数$K(\cdot )$以及窗宽$h_n>0$,
  $$\inf K(u)\mathrm{d}\mathrm{u}=1.$$
• 定义加权平均核为
  $${\omega }_i(x)=\frac{K_{h_n}(X_i-x)}{{\sum }_{j=1}^n{K}_{h_n}(X_j-x)},i=1,2,\cdots ,n,$$
  其中$K_{h_n}(u)=h_n^{-1}K(u{h}_n^{-1})$是一个概率密度函数.则N-W估计的定义为:
  $$\widehat{m_n(x)=\sum _{i=1}^n}{\omega }_i(x)Y_i.$$
  注意一点：
  $$\hat{\theta }=\underset{\theta }{\min }\sum _{i=1}^n{\omega }_i(x)(Y_i-\theta {)}^2=\sum _{i=1}^n\frac{{\omega }_i{Y}_i}{{\sum }_{i=1}^n{\omega }_i},$$
  因此,核估计等价于局部加权最小二乘估计.权重${\omega }_i=K(X_i-x)$.常用核函数已经在上篇文章介绍.核密度回归还有另外一种写法:
  $$E(Y|X=x)=\int yf(y|x)dy=\int y\frac{f(x,y)}{f_X(x)}dy=m(x),$$
  其中$f(y|x)$是给定$X=x$时$Y$的条件pdf,$f_X(x)$是$X$的边际pdf.上式对$y$积分所以可以进一步写为:
  $$m(x)=E(Y|X=x)=\frac{\int yf(x,y)dy}{f_X(x)}.$$
  给定样本观测值为{Xi,Yi},i=1,…,n\{X_i,Y_i\},i=1,\dots,n{Xi​,Yi​},i=1,…,n.此时的未知量是$f(x,y)$和$f_X(x)$,我们可以通过多元核密度估计来得到,此时有:
  $${\hat{f}}_{h,g}(x,y)=\frac{1}{n}\sum _{i=1}^n{K}_h\left(\frac{x-X_i}{h}\right)K_g\left(\frac{y-Y_i}{g}\right)$$
  令$\frac{(y-Y_i)}{g}=s$:
  $$\begin{array}{rl}\int y{\hat{f}}_{h,g}(x,y)dy& =\frac{1}{n}\sum _{i=1}^n\frac{1}{h}K\left(\frac{x-X_i}{h}\right)\int \frac{y}{g}{K}_g\left(\frac{y-Y_i}{g}\right)dy\\ & =\frac{1}{n}\sum _{i=1}^n{K}_h(x-X_i)\int (sg+Y_i)K(s)ds\\ & =\frac{1}{n}{K}_h(x-X_i)\left\{g\int sK(s)ds+Y_i\int K(s)ds\right\}\\ & =\frac{1}{n}{K}_h(x-X_i)Y_i\end{array}$$
  其中由核函数的性质得到:$\int sK(s)ds=E(s)=0$,$\int K(s)ds=1$则Nadaraya-Watson估计量还可以写为:
  $${\hat{m}}_h(x)=\frac{n^{-1}{\sum }_{i=1}^n{K}_h(x-X_i)Y_i}{n^{-1}{\sum }_{j=1}^n{K}_h(x-X_j)}$$
  举个例子：
  
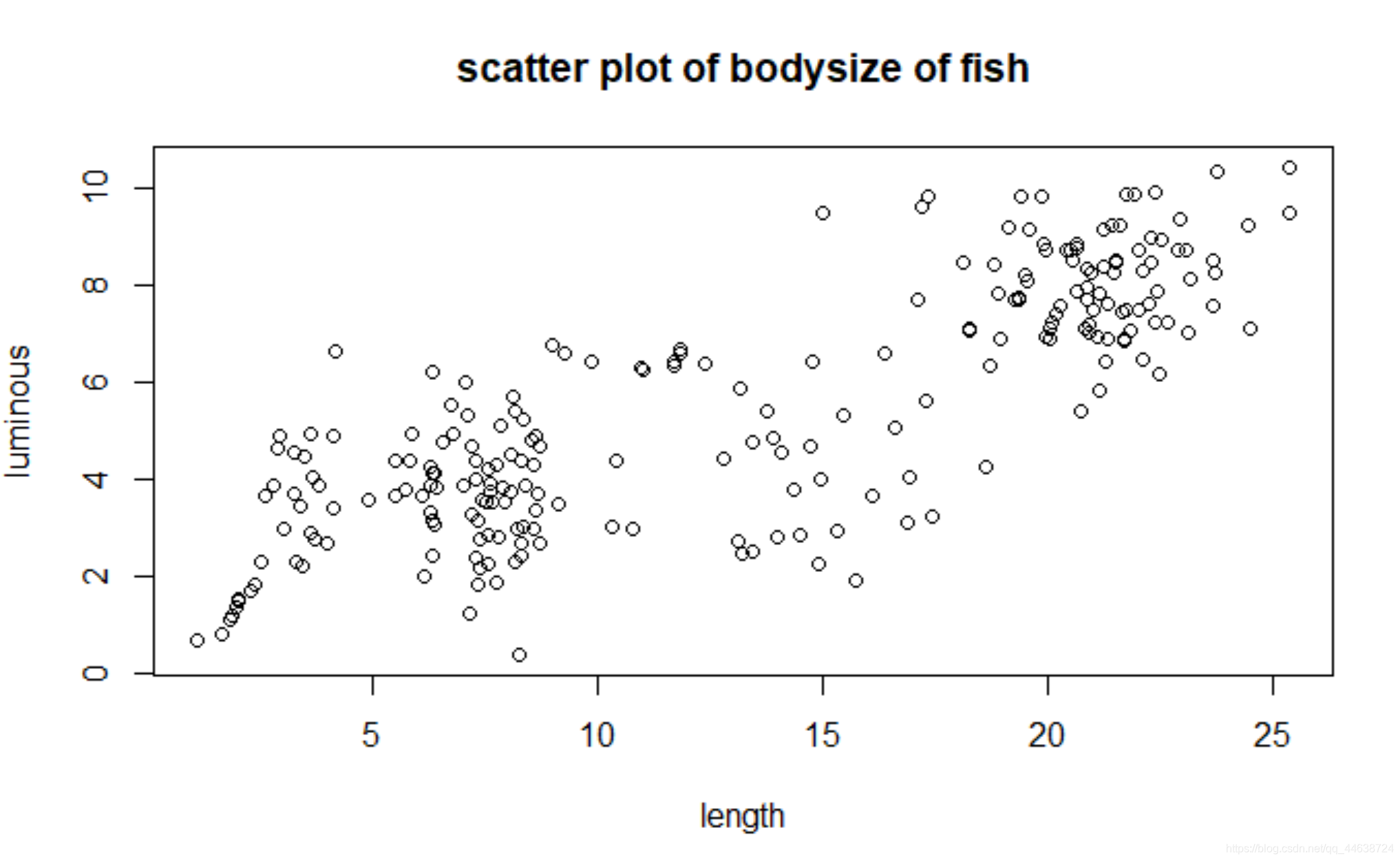
  我们通过一元核回归模型来拟合这个数据集,采用$Nadaraya-Watson$核回归,同时比较不同窗宽$h$对回归曲线的影响,首先复习一下上节的二元核密度估计:
  
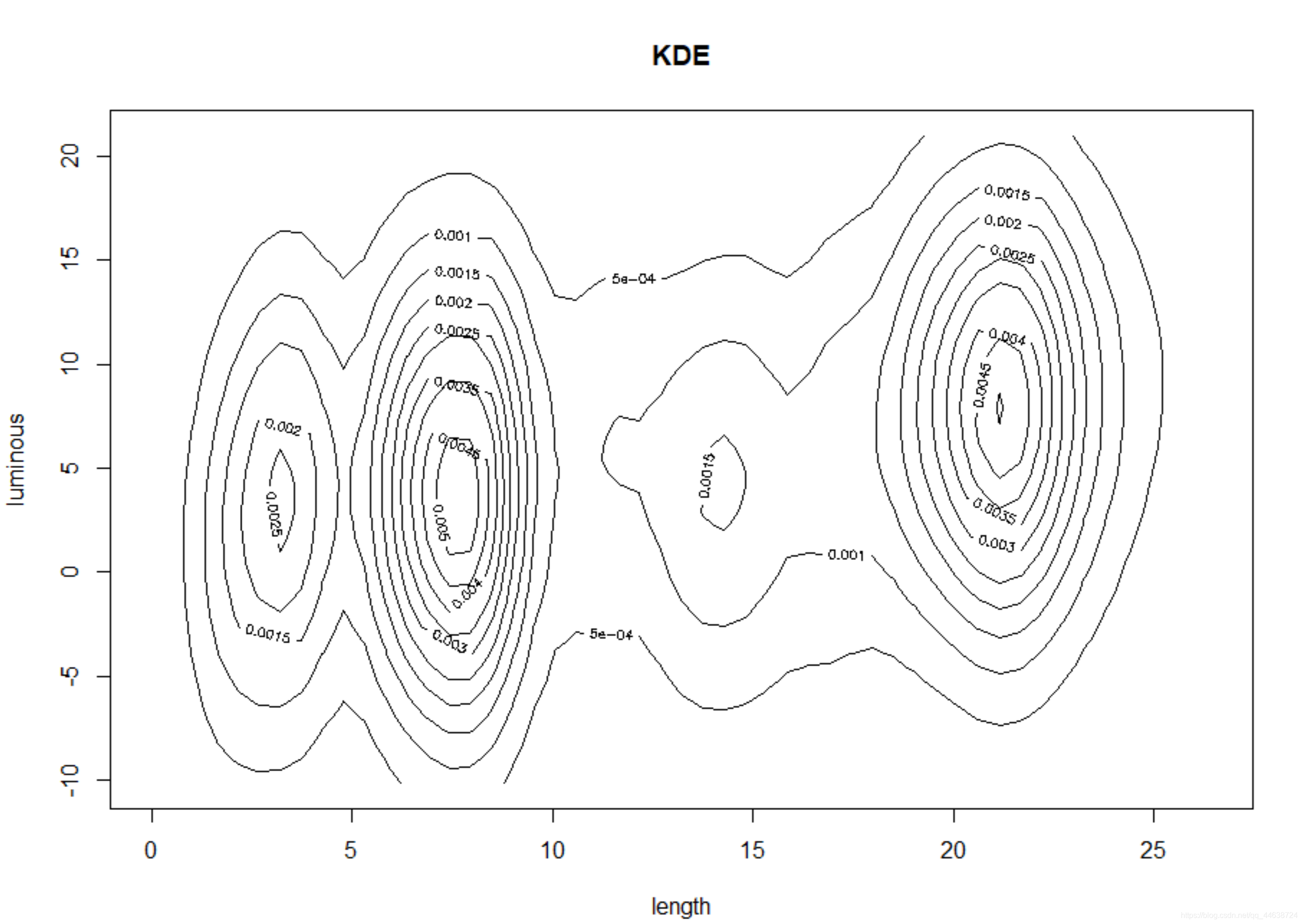
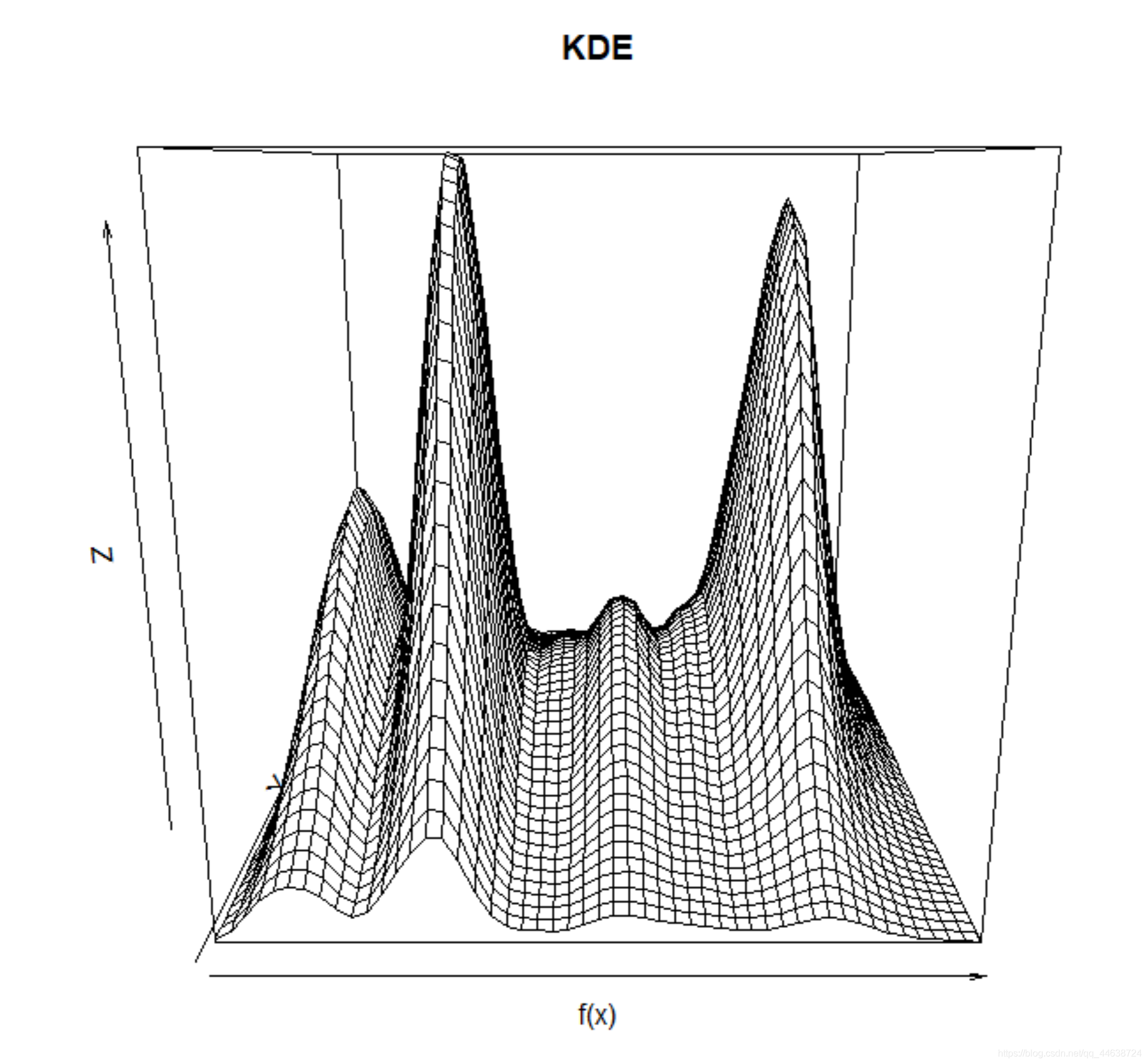
  再看看另一个角度：

代码如下

file = "D:\REF\fish.txt"
data<-read.table(file="D:\\REF\\fish.txt",header = T)
x <- cbind(data$length,data$luminous)

est <- bkde2D(x=x)
contour(est$x1, est$x2, est$fhat,xlab = 'length',ylab='luminous',main='KDE')
persp(est$fhat,xlab = 'f(x)',main = 'KDE')

再进行核回归,这里分别取$h=0.1,0.5,1.5,3.0$.

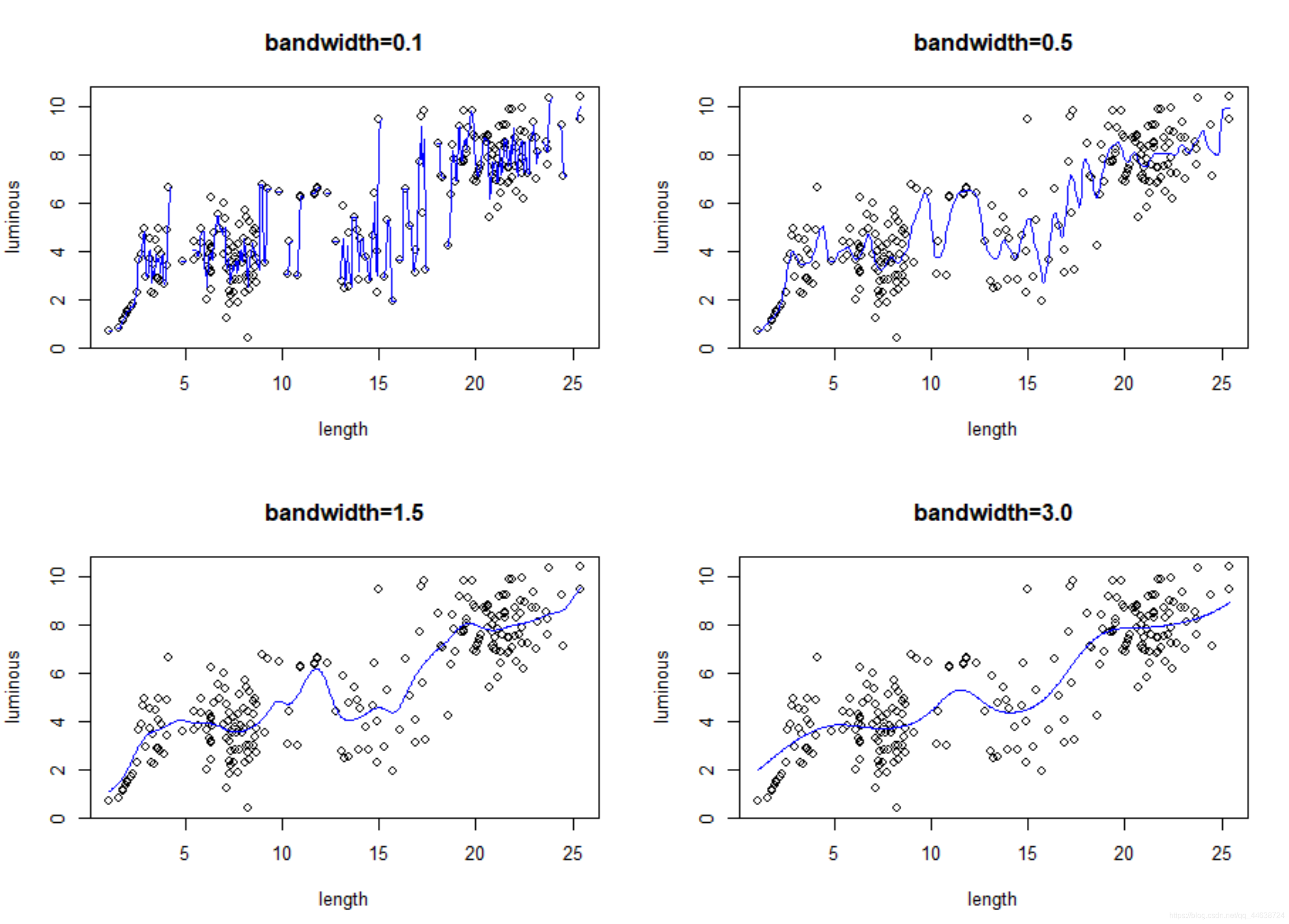
R语言代码如下

file = "D:\REF\fish.txt"
data<-read.table(file="D:\\REF\\fish.txt",header = T)
x <- cbind(data$length,data$luminous)

par(mfrow=c(2,2))
fit1 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 0.1,range.x = range(data$length),n.points = length(x))
fit2 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 0.5,range.x = range(data$length),n.points = length(x))
fit3 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 1.5,range.x = range(data$length),n.points = length(x))
fit4 <- ksmooth(x=data$length,y=data$luminous,kernel='normal',bandwidth = 3.0,range.x = range(data$length),n.points = length(x))
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=0.1')
lines(fit1,lwd=1.0,col='blue')
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=0.5')
lines(fit2,lwd=1.0,col='blue')
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=1.5')
lines(fit3,lwd=1.0,col='blue')
plot(x1,x2,xlab = 'length' ,ylab = 'luminous' ,main='bandwidth=3.0')
lines(fit4,lwd=1.0,col='blue')