解决农夫约翰如何为N头牛同时分配F种食物和D种饮料的问题，使用最大流算法，包括EdmondsKarp、Dinic和ISAP三种算法实现。
Dining POJ - 3281
题意：农夫约翰为他的N头牛准备了F种食物和D种饮料。每头牛都有各自喜欢的食物和饮料，而每种食物或饮料只能分配给一头牛。最多能有多少头牛同时得到自己喜欢的食物和饮料？
题解：如果只是分配食物的话，那么用二分图最大匹配就好了，但遇到这种情况需要同时给一头牛分配所喜欢的食物和饮料的情况，就不能很好的处理了，可以将食物和饮料所对应的两个匹配通过下面这种方法匹配起来。
图的顶点在食物对应的匹配中的食物和牛，饮料对应的匹配中的饮料和牛之外，还有一个源点s和一个汇点t。
在两个匹配相同的牛之间连一条边，在s和所有食物，t和所有饮料之间连一条边。
边的方向为s->食物->牛->牛->饮料->t，容量全都为1。
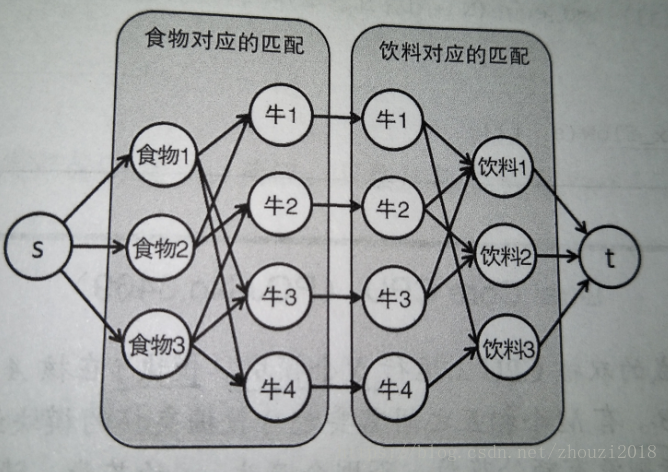
这个图中的每一条s-t路径都对应一个牛的食物和饮料的分配方案。我们把食物所对应的牛和饮料所对应的牛拆成两个顶点，之间连一条容量为1的边，就保证了一头牛不会被分配多组食物和饮料。只要计算该图中的最大流，问题就解决了。
下面给出三种算法的AC代码：
EdmondsKarp算法
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
using namespace std;
const int maxn = 1008;
const int INF = 111111111;
struct Edge{
int from,to,cap,flow;
Edge(int u,int v,int c,int f):from(u),to(v),cap(c),flow(f){}
};
int s,t;
struct EdmondsKarp{
int n,m;
vector<Edge>edge; //边数的两倍
vector<int>G[maxn]; //邻接表，G[i][j]表示i的第j条边在e数组中的序号
int a[maxn]; //当起点到i的可改进量
int p[maxn]; //最短路树上p的入弧编号
void init(int n){
for(int i=0;i<=n;i++) G[i].clear();
edge.clear();
}
void AddEdge(int from,int to,int cap){
edge.push_back(Edge(from,to,cap,0));
edge.push_back(Edge(to,from,0,0)); //反向弧
m=edge.size();
G[from].push_back(m-2);
G[to].push_back(m-1);
}
int Maxflow(int s,int t){
int flow=0;
for(;;){
memset(a,0,sizeof(a));
queue<int>q;
while(!q.empty()) q.pop();
q.push(s);
a[s]=INF;
while(!q.empty()){
int x=q.front();q.pop();
for(int i=0;i<G[x].size();i++){
Edge& e=edge[G[x][i]];
if(!a[e.to]&&e.cap>e.flow){
p[e.to]=G[x][i];
a[e.to]=min(a[x],e.cap-e.flow);
q.push(e.to);
}
}
if(a[t]) break;
}
if(!a[t]) return flow;
for(int u=t;u!=s;u=edge[p[u]].from){
edge[p[u]].flow+=a[t];
edge[p[u]^1].flow-=a[t];
}
flow+=a[t];
}
}
};
int main()
{
int N,F,D;
s = 0;
while(~scanf("%d%d%d",&N,&F,&D))
{
EdmondsKarp EK;
t = N*2+F+D+1;
EK.init(t+1);
int f,d;
for(int i = 1; i <= F; i++){//源点向各种食物连边
EK.AddEdge(s,i,1);
}
int tm;
for(int i = 1; i <= N; i++){
scanf("%d%d",&f,&d);
for(int j = 1; j <= f; j++){
scanf("%d",&tm);
EK.AddEdge(tm,F+i*2-1,1);//食物向喜欢它的牛连边
}
EK.AddEdge(F+i*2-1,F+i*2,1);//牛拆点
for(int j = 1; j <= d; j++){
scanf("%d",&tm);
EK.AddEdge(F+i*2,2*N+F+tm,1);//牛向喜欢的饮料连边
}
}
for(int i = 1; i <= D; i++){
EK.AddEdge(2*N+F+i,t,1);//所有饮料向汇点连边
}
//puts("haha");
int ans = EK.Maxflow(0,t);
printf("%d\n",ans);
}
return 0;
}
/*
_ooOoo_
o8888888o
88" . "88
(| -_- |)
O\ = /O
____/`---'\____
.' \\| |// `.
/ \\||| : |||// \
/ _||||| -:- |||||- \
| | \\\ - /// | |
| \_| ''\---/'' | |
\ .-\__ `-` ___/-. /
___`. .' /--.--\ `. . __
."" '< `.___\_<|>_/___.' >'"".
| | : `- \`.;`\ _ /`;.`/ - ` : | |
\ \ `-. \_ __\ /__ _/ .-` / /
======`-.____`-.___\_____/___.-`____.-'======
`=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
The program have no BUG.
*/
Dinic算法
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<map>
#define E 1e-9
#define LL long long
using namespace std;
const int MAX_N=150;
const int MAX_D=150;
const int MAX_F=150;
const int MAX_V=1000;
const int INF=0x3f3f3f3f;
int N,F,D;
int likeF[MAX_N][MAX_F];
int likeD[MAX_N][MAX_D];
struct edge{
int to,cap,rev;
edge(int _to,int _cap,int _rev):to(_to),cap(_cap),rev(_rev){}
};
vector<edge>G[MAX_V];
int level[MAX_V];
int iter[MAX_V];
void add_edge(int from,int to,int cap)
{
G[from].push_back(edge(to,cap,G[to].size()));
G[to].push_back(edge(from,0,G[from].size()-1));
}
void bfs(int s)
{
memset(level,-1,sizeof(level));
queue<int>que;
level[s]=0;
que.push(s);
while(!que.empty())
{
int v=que.front();
que.pop();
for(int i=0;i<G[v].size();i++)
{
edge &e=G[v][i];
if(e.cap>0&&level[e.to]<0)
{
level[e.to]=level[v]+1;
que.push(e.to);
}
}
}
}
int dfs(int v,int t,int f)
{
if(v==t)
return f;
for(int &i=iter[v];i<G[v].size();i++)
{
edge &e=G[v][i];
if(e.cap>0&&level[v]<level[e.to])
{
int d=dfs(e.to,t,min(f,e.cap));
if(d>0)
{
e.cap-=d;
G[e.to][e.rev].cap+=d;
return d;
}
}
}
return 0;
}
int max_flow(int s,int t)
{
int flow=0;
for(;;)
{
bfs(s);
if(level[t]<0)
return flow;
memset(iter,0,sizeof(iter));
int f;
while((f=dfs(s,t,INF))>0)
flow+=f;
}
}
void solve()
{
int s=N*2+F+D,t=s+1;
for(int i=0;i<F;i++)
add_edge(s,N*2+i,1);
for(int i=0;i<D;i++)
add_edge(N*2+F+i,t,1);
for(int i=0;i<N;i++)
{
add_edge(i,N+i,1);
for(int j=0;j<F;j++)
if(likeF[i][j])
add_edge(N*2+j,i,1);
for(int j=0;j<D;j++)
if(likeD[i][j])
add_edge(N+i,N*2+F+j,1);
}
printf("%d\n",max_flow(s,t));
}
int main()
{
scanf("%d%d%d",&N,&F,&D);
int cntf,cntd;
for(int i=0;i<N;i++)
{
scanf("%d%d",&cntf,&cntd);
int temp;
for(int j=0;j<cntf;j++)
{
scanf("%d",&temp);
temp--;
likeF[i][temp]=1;
}
for(int j=0;j<cntd;j++)
{
scanf("%d",&temp);
temp--;
likeD[i][temp]=1;
}
}
solve();
return 0;
}
/*
_ooOoo_
o8888888o
88" . "88
(| -_- |)
O\ = /O
____/`---'\____
.' \\| |// `.
/ \\||| : |||// \
/ _||||| -:- |||||- \
| | \\\ - /// | |
| \_| ''\---/'' | |
\ .-\__ `-` ___/-. /
___`. .' /--.--\ `. . __
."" '< `.___\_<|>_/___.' >'"".
| | : `- \`.;`\ _ /`;.`/ - ` : | |
\ \ `-. \_ __\ /__ _/ .-` / /
======`-.____`-.___\_____/___.-`____.-'======
`=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
The program have no BUG.
*/
*ISAP算法
算法思路：
只一次bfs和dfs动态更新标号值,bfs给每个点一个层数值（当前点到汇点的距离），然后dfs通过层数的限制一次可以更新多条增广路，来寻找最大流。这里注意，dfs过程中动态更新标号值，如果当前的这个点到汇点的边的残余流量值为0说明这个点不能再通过这个边到达汇点，所以要将这个点的标号标记为它链接的孩子的节点中标号最小的那个的标号值+1，具体的可以画个图来看一下。
这个算法之所以快，是因为可以加一个gap优化，即设一个数组保存标号为i的节点个数为d[i]这样在d[i]出现在0<i<n0<i<n的时候有d[i]==0则这个时候直接结束即可，说明从汇点已经不能到达源点了。已经没有增广路了
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <queue>
using namespace std;
const int inf = 0x3fffffff;
template <int N, int M>
struct Isap
{
int top;
int d[N], pre[N], cur[N], gap[N];
struct Vertex{
int head;
} V[N];
struct Edge{
int v, next;
int c, f;
} E[M];
void init(){
memset(V, -1, sizeof(V));
top = 0;
}
void add_edge(int u, int v, int c){
E[top].v = v;
E[top].c = c;
E[top].f = 0;
E[top].next = V[u].head;
V[u].head = top++;
}
void add(int u,int v, int c){
add_edge(u, v, c);
add_edge(v, u, 0);
}
void set_d(int t){
queue<int> Q;
memset(d, -1, sizeof(d));
memset(gap, 0, sizeof(gap));
d[t] = 0;
Q.push(t);
while(!Q.empty()) {
int v = Q.front(); Q.pop();
++gap[d[v]];
for(int i = V[v].head; ~i; i = E[i].next) {
int u = E[i].v;
if(d[u] == -1) {
d[u] = d[v] + 1;
Q.push(u);
}
}
}
}
int sap(int s, int t, int num) {
set_d(t);
int ans = 0, u = s;
int flow = inf;
memcpy(cur, V, sizeof(V));
while(d[s] < num) {
int &i = cur[u];
for(; ~i; i = E[i].next) {
int v = E[i].v;
if(E[i].c > E[i].f && d[u] == d[v] + 1) {
u = v;
pre[v] = i;
flow = min(flow, E[i].c - E[i].f);
if(u == t) {
while(u != s) {
int j = pre[u];
E[j].f += flow;
E[j^1].f -= flow;
u = E[j^1].v;
}
ans += flow;
flow = inf;
}
break;
}
}
if(i == -1) {
if(--gap[d[u]] == 0)
break;
int dmin = num - 1;
cur[u] = V[u].head;
for(int j = V[u].head; ~j; j = E[j].next)
if(E[j].c > E[j].f)
dmin = min(dmin, d[E[j].v]);
d[u] = dmin + 1;
++gap[d[u]];
if(u != s)
u = E[pre[u] ^ 1].v;
}
}
return ans;
}
};
Isap<1000, 1000000> Sap;
int main()
{
int N,F,D;
int s, t, num;
while(~scanf("%d%d%d",&N,&F,&D))
{
t = N*2+F+D+1;
s = 0;
num = t+1;
Sap.init();
int f,d;
for(int i = 1; i <= F; i++){//源点向各种食物连边
Sap.add(s,i,1);
}
int tm;
for(int i = 1; i <= N; i++){
scanf("%d%d",&f,&d);
for(int j = 1; j <= f; j++){
scanf("%d",&tm);
Sap.add(tm,F+i*2-1,1);//食物向喜欢它的牛连边
}
Sap.add(F+i*2-1,F+i*2,1);//牛拆点
for(int j = 1; j <= d; j++){
scanf("%d",&tm);
Sap.add(F+i*2,2*N+F+tm,1);//牛向喜欢的饮料连边
}
}
for(int i = 1; i <= D; i++){
Sap.add(2*N+F+i,t,1);//所有饮料向汇点连边
}
//puts("haha");
int ans = Sap.sap(s,t,num);
printf("%d\n",ans);
}
return 0;
}
/*
_ooOoo_
o8888888o
88" . "88
(| -_- |)
O\ = /O
____/`---'\____
.' \\| |// `.
/ \\||| : |||// \
/ _||||| -:- |||||- \
| | \\\ - /// | |
| \_| ''\---/'' | |
\ .-\__ `-` ___/-. /
___`. .' /--.--\ `. . __
."" '< `.___\_<|>_/___.' >'"".
| | : `- \`.;`\ _ /`;.`/ - ` : | |
\ \ `-. \_ __\ /__ _/ .-` / /
======`-.____`-.___\_____/___.-`____.-'======
`=---='
^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
The program have no BUG.
*/
扫一扫
425
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
