并查集-----个人总结

什么是并查集？
英文：Disjoint Set ，即 “ 不相交集合 ”
将编号分别为1…N的N个对象划分为不相交集合，
在每个集合中，选择集中某个元素代表所在集合
常见两种操作：

1. 合并两个集合
2. 查找某元素属于哪个集合
   所以，称为 “ 并查集 ”

并查集的应用：

1. 并查集 可用于查询 网络 中两个节点的状态， 这里的网络是一个抽象的概念， 不仅仅指互联网中的网络， 也可以是人际关系的网络、交通网络等。

2. 并查集 除了可以用于查询 网络 中两个节点的状态， 还可以用于数学中集合相关的操作， 如求两个集合的并集等。

3. 并查集 对于查询两个节点的 连接状态 非常高效。对于两个节点是否相连，也可以通过求解 查询路径 来解决， 也就是说如果两个点的连接路径都求出来了，自然也就知道两个点是否相连了，但是如果仅仅想知道两个点是否相连，使用 路径问题 来处理效率会低一些，并查集 就是一个很好的选择。

普通并查集：

一：若某个家族人员过于庞大，要判断两个是否是亲戚，确实不容易，给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。
规定：x和y是亲戚，y和z是亲戚，那么x和z也是亲戚。如果x,y是亲戚，那么x的亲戚都是y的亲戚，y的亲戚也都是x的亲戚。
样例输入：
9 7 1
2 4
5 7
1 3
8 9
1 2
5 6
2 3
1 9
我们可以这样解决：
我们可以给每个人建立一个集合，集合的元素值有他自己，表示最开始时他不知道任何人是它的亲戚。以后每次给出一个亲戚关系a, b，则a和他的亲戚与b和他的亲戚就互为亲戚了，将a所在集合与b所在集合合并。对于样例数据的操作全过程如下：
初始状态：

{1} {2} {3} {4} {5} {6} {7} {8} {9}

输入关系 分离集合

(2,4) {2,4}{1} {3} {5} {6} {7} {8} {9}
(5,7) {2,4} {5,7} {1} {3} {6} {8} {9}
(1,3) {1,3} {2,4} {5,7}{6} {8} {9}
(8,9) {1,3} {2,4} {5,7} {8,9}{6}
(1,2) {1,2,3,4} {5,7} {8,9}{6}
(5,6) {1,2,3,4} {5,6,7} {8,9}
(2,3) {1,2,3,4} {5,6,7} {8,9}
判断亲戚关系
(1,9)，
因为1,9不在同一集合内，所以输出"NO"。
最后我们得到3个集合{1,2,3,4}、{5,6,7}、{8,9}，于是判断两个人是否亲戚的问题就变成判断两个数是否在同一个集合中的问题。如此一来，需要的数据结构就没有图结构那样庞大了。
具体例题：
1.畅通工程：
题目链接：
http://acm.hdu.edu.cn/showproblem.php?pid=1232

int f[1010];//存储父节点
void init()//初始化
{
for (int i = 1; i <= 100; i++)
 f[i] = i;//一开始节点i根节点当然是i啦
}
int find1(int i)
{
if(i!=f[i])
{
f[i]=find1(f[i]);//没到头就继续往下找
}
return f[i];
}
void merge(int i, int j)//压缩路径
{
int fx=find1(i);
int fy=find1(j);
if(f[fx]!=f[fy])
{
f[fy]=fx;/*合并直接让一个集合的根节点连向另一个根节点就行，毕竟根节点就是一个集合的标志*/
}
}

种类并查集：
一般的并查集是维护属于同一种类的元素，对于属于不同种类的元素之间的关系没有记录。种类并查集就是同一集合中的元素是已经确定关系的（是否属于同一种类）
这里用的结构体：

struct  node
{
   int parent;//p[i].parent表示节点i的父节点
   int relation;//p[i].relation表示节点i与其父节点
}p[20005];

此处relation有三种取值(假设节点x的父节点为rootx,即p[x].parent=root)：

1. p[x].relation=0 ……表示节点x与其父节点rootx的关系是：同类
2. p[x].relation=1 ……表示节点x与其父节点rootx的关系是：被根结点吃
3. p[x].relation=2 ……表示节点x与其父节点rootx的关系是：吃根结点

初始化函数：

void init(int n)
{
	int i;
	for(i = 1;i <= n; ++i)
	{
		p[i].parent = i;            //初始时集合编号就设置为自身
		p[i].relation = 0;        //因为p[i].parent=i,即节点i的父亲节点   就是自身,所以此时节点i与其父亲节点的关系为同类(即p[i].relation=0)
	}
}

下面详细讲解并查集的两个重要操作:查找和合并.

查找操作：
在查找时因为节点不仅有父亲节点域,而且还有表示节点与其父亲节点的关系域,查找过程中对父亲节点域的处理和简单的并查集处理一样,即在查找过程中同时实现路径压缩,但正是由于路径压缩,使得表示节点与其父亲节点的关系域发生了变化,所以在路径压缩过程中节点和其对应的父节点的关系域发生了变化(因为路径压缩之前节点x的父亲节点为rootx的话,那么在路径压缩之后节点x的父亲节点就变为了节点rootx的父亲节点rootxx,所以此时p[x].relation存储的应该是节点x与现在父亲节点rootxx的关系),此处可以画图理解一下:
查找之前的集合：

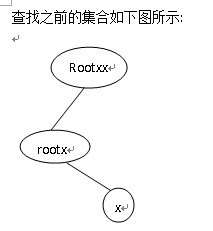
查找之后的集合：

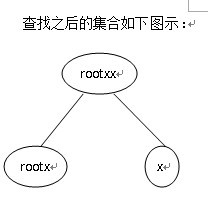
很明显查找之前节点x的父亲节点为rootx,假设此时p[x].relation=1(即表示x的父亲节点rootx吃x)且p[rootx].relation=0(即表示rootx和其父亲节点rootxx是同类),由这两个关系可以推出rootxx吃x,而合并以后节点x的父亲节点为rootxx(实现了路径压缩),且节点x的父亲节点rootxx吃x,即查找之后p[x].relation=1。

合并操作：

在将元素x与y所在的集合合并时,假设元素x所在的集合编号为rootx,元素y所在的集合编号为rooty,合并时直接将集合rooty挂到集合rootx上,即p[rooty].parent=rootx,此时原来集合rooty中的根节点rooty的关系域也应随之发生变化,因为合并之前rooty的父亲节点就是其自身,故此时p[rooty].relation=0,而合并之后rooty的父亲节点为rootx,所以此时需判断rootx与rooty的关系,即更新p[rooty]的值,同理画图理解:

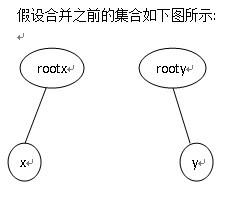
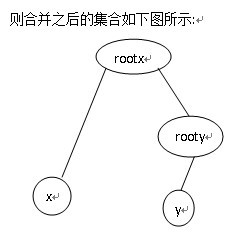
此时假设假设p[x].relation=0(即x与rootx的关系是同类),p[y].relation=1(即rooty吃y),则有:
1>输入d=1时,即输入的x和y是同类,则有上述关系可以推出rooty吃rootx,即p[rooty].relation=2;
2>输入d=2时,即输入的x吃y,则有上述关系可以推出rooty与rootx是同类(因为rooty吃y,x吃y,则rooty与x是同类,又rootx与x是同类),即p[rooty].relation=0;
当然,这只是一种可能,其它的可能情况和上面一样分析。

当元素x与元素y在同一集合时,则不需要合并,因为此时x与y的父亲节点相同,可以分情况讨论:
1>d=1时,即x与y是同类时,此时要满足这要求,则必须满足p[x].relation=p[y].relation,这很容易推出来.
2>d=2时,即表示x吃y,此时要满足这要求,则也必须满足一定的条件,如x和root是同类(即p[x].relation=0),此时要满足x吃y,则必须满足root吃y,即p[y].relation=1,可以像上面一样画图来帮助理解.

关系域更新：

当然，这道题理解到这里思路已经基本明确了，剩下的就是如何实现，在实现过程中，我们发现，更新关系域是一个很头疼的操作，网上各种分析都有，但是都是直接给出个公式，至于怎么推出来的都是一笔带过，让我着实头疼了很久，经过不断的看discuss，终于明白了更新操作是通过什么来实现的。下面讲解一下
仔细再想想，rootx-x 、x-y、y-rooty，是不是很像向量形式?于是我们可以大胆的从向量入手：

tx ty

| |

x ~ y

对于集合里的任意两个元素x，y而言，它们之间必定存在着某种联系，因为并查集中的元素均是有联系的（这点是并查集的实质，要深刻理解），否则也不会被合并到当前集合中。那么我们就把这2个元素之间的关系量转化为一个偏移量（大牛不愧为大牛！~YM）。

由上面可知：
x->y 偏移量0时 x和y同类

x->y 偏移量1时 x被y吃

x->y 偏移量2时 x吃y

有了这个假设，我们就可以在并查集中完成任意两个元素之间的关系转换了。

不妨继续假设，x的当前集合根节点rootx，y的当前集合根节点rooty，x->y的偏移值为d-1（题中给出的询问已知条件）

(1)如果rootx和rooty不相同，那么我们把rooty合并到rootx上，并且更新relation关系域的值（注意：p[i].relation表示i的根结点到i的偏移量！！！！（向量方向性一定不能搞错））

此时 rootx->rooty = rootx->x + x->y + y->rooty，这一步就是大牛独创的向量思维模式
上式进一步转化为：rootx->rooty = (relation[x]+d-1+3-relation[y])%3 = relation[rooty]，（模3是保证偏移量取值始终在[0,2]间）

(2)如果rootx和rooty相同(即x和y在已经在一个集合中，不需要合并操作了，根结点相同)，那么我们就验证x->y之间的偏移量是否与题中给出的d-1一致
此时 x->y = x->rootx + rootx->y
上式进一步转化为：x->y = (3-relation[x]+relation[y])%3，
若一致则为真，否则为假。

代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 50010
 
struct node
{
	int pre;
	int relation;
};
node p[N];
 
int find(int x) //查找根结点
{
	int temp;
	if(x == p[x].pre)
		return x;
	temp = p[x].pre; //路径压缩
	p[x].pre = find(temp);
	p[x].relation = (p[x].relation + p[temp].relation) % 3; //关系域更新
	return p[x].pre; //根结点
}
 
int main()
{
	int n, k;
	int ope, a, b;
	int root1, root2;
	int sum = 0; //假话数量
	scanf("%d%d", &n, &k);
	for(int i = 1; i <= n; ++i) //初始化
	{
		p[i].pre = i;
		p[i].relation = 0;
	}
	for(int i = 1; i <= k; ++i)
	{
		scanf("%d%d%d", &ope, &a, &b);
		if(a > n || b > n) //条件2
		{
			sum++;
			continue;
		}
		if(ope == 2 && a == b) //条件3
		{
			sum++;
			continue;
		}
		root1 = find(a);
		root2 = find(b);
		if(root1 != root2) // 合并
		{
			p[root2].pre = root1;
			p[root2].relation = (3 + (ope - 1) +p[a].relation - p[b].relation) % 3;
		}
		else
		{
			if(ope == 1 && p[a].relation != p[b].relation)
			{
				sum++;
				continue;
			}
			if(ope == 2 && ((3 - p[a].relation + p[b].relation) % 3 != ope - 1))
			{
				sum++;
				continue;}
		}
	}
	printf("%d\n", sum);
	return 0;
}

经典例题：
食物链：
题目链接：
https://cn.vjudge.net/problem/POJ-1182

动物王国中有三类动物A,B,C，这三类动物的食物链构成了有趣的环形。A吃B， B吃C，C吃A。
现有N个动物，以1－N编号。每个动物都是A,B,C中的一种，但是我们并不知道它到底是哪一种。
有人用两种说法对这N个动物所构成的食物链关系进行描述：
第一种说法是"1 X Y"，表示X和Y是同类。
第二种说法是"2 X Y"，表示X吃Y。
此人对N个动物，用上述两种说法，一句接一句地说出K句话，这K句话有的是真的，有的是假的。当一句话满足下列三条之一时，这句话就是假话，否则就是真话。
1） 当前的话与前面的某些真的话冲突，就是假话；
2） 当前的话中X或Y比N大，就是假话；
3） 当前的话表示X吃X，就是假话。
你的任务是根据给定的N（1 <= N <= 50,000）和K句话（0 <= K <= 100,000），输出假话的总数。
Input
第一行是两个整数N和K，以一个空格分隔。
以下K行每行是三个正整数 D，X，Y，两数之间用一个空格隔开，其中D表示说法的种类。
若D=1，则表示X和Y是同类。
若D=2，则表示X吃Y。
Output
只有一个整数，表示假话的数目。
Sample Input
100 7
1 101 1
2 1 2
2 2 3
2 3 3
1 1 3
2 3 1
1 5 5
Sample Output
3
题目关键代码：

int d1[100005];
int r[99999];//存储各个动物之间的关系， 0表示同类，1表示吃父节点，2表示被父节点吃
int find1(int x)
{
    int fx=x;
    if(x!=d1[x])
    {
        fx=find1(d1[x]);
        r[x]=(r[x]+r[d1[x]])%3;//
        d1[x]=fx;
    }
    return d1[x];
}
int uoion(int d,int x,int y)
{
    int fx=find1(x);
    int fy=find1(y);
    if(fx!=fy)
    {
        d1[fy]=d1[x];
        r[fy]=(3-r[y]+d-1+r[x])%3;//
        return 0;
    }
    if((r[y]-r[x]+3)%3!=d-1)
        return 1;
    return 0;
}