线性表属于线性结构,是属于同一数据对象的元素组成的有限序列。它在逻辑结构上属于线性结构,在存储结构上可以分别用顺序存储结构和链式存储结构来表示。
顺序存储
1.线性表的顺序存储结构的表示(又称顺序表)
用顺序地址存储的方式映射线性表的逻辑结构,即用一组地址连续的存储单元依次存储线性表的数据元素。
每一个数据元素存储位置和线性表的起始位置对应一个唯一常数和存储单元来确定,即为随机存取的存储结构,常用变长数组来表示。
代码实现
设计顺序表ADT的接口头文件
///Squence.h
#pragma once
#include<stdbool.h>
#include<stdio.h>
#define MAX 100 //顺序表最大值
//顺序表数据元素(更改数据元素,修改基本元素结构体和接口的实现即可)
struct item{
//数据项
char no[20];
char name[40];
float price;
bool operator==(const item& a) {
return (no == a.no) && (name == a.name) && (price == a.price);
}
};
typedef item Item;
typedef struct {
Item* link;
int length;
}SquenceList;
typedef SquenceList* List;
//顺序表初始化
bool Listinit(List L);
//顺序表取值
bool GetItem(const List L, int i, Item &e);
//顺序表查找
int LocateItem(const List L, Item e);
//顺序表插入
bool ListInsert(List L, int i, Item e);
//顺序表展示
bool Listshow(List L);
接口的实现
#include<stdio.h>
#include<stdlib.h>
#include"Squence.h"
//顺序表初始化
bool Listinit(List L) {
L->link = new Item[MAX]; //初始化存储空间大小固定,容易浪费大量存储空间
if (!L->link) {
fputs("overflow", stderr);
return false;
}
L->length = 0;
return true;
}
//顺序表取值
bool GetItem(const List L, int i,Item &e) {
if (i<1 || i>L->length) {
fputs("overflow", stderr);
return false;
}
else {
e = L->link[i-1]; //时间复杂度为O(1)
return true;
}
}
//顺序表查找
int LocateItem(const List L, Item e) {
for (int i = 0; i < L->length; ++i) { //ASL为(n+1)/2,则时间复杂度为O(n)
if (L->link[i] == e)
return i + 1;
}
return 0;
}
//顺序表插入
bool ListInsert(List L, int i, Item e) {
if (L->length == MAX) {
fputs("number overflow\n", stderr);
return false;
}
else if ((i < 1) || i > L->length + 1) {
fputs("number input error\n", stderr);
return false;
}
else {
for (int j = L->length-1; j >= i-1; --j) { //E(移动元素的期望)=n/2,即时间复杂度为O(n)
L->link[j] = L->link[j + 1];
}
L->link[i - 1] = e;
++L->length;
return true;
}
}
void Output(List L) {
if (L->length) {
for (int i = 0; i < L->length; ++i) {
printf("the no : %s\n", L->link[i].no);
printf("the name : %s\n", L->link[i].name);
printf("the price: %.2f\n", L->link[i].price);
}
}
}
主函数测试
///test.c
#include<stdio.h>
#include<stdlib.h>
#include"Squence.h"
int main(int agrc, char* argv[]) {
extern void Output(List L);
SquenceList node;
Listinit(&node);
item e;
e = { "1023","the star",21.22 };
ListInsert(&node, 1, e);
Output(&node);
return 0;
}
/*
*vs2019输出
the no : 1023
the name : the star
the price: 21.22
D:\vs\Data_Struct\Debug\Data_Struct.exe (进程 1240)已退出,代码为 0。
按任意键关闭此窗口. . .
*/
链式存储
1.线性表的链式存储结构的表示
用链式地址存储的方式映射线性表的逻辑结构,即用一个结点来表示一个数据元素的存储映像,其中的数据域表示数据元素信息,指针域存储后继存储位置的信息。
多个结点组成的俩存储映像链结成一条链表,即为顺序存取的存储方式,常用单链表、循环链表和双向链表来表示。
代码实现
本文实现不带头结点的单链表。
实现单链表ADT
///link.h
#pragma once
#include<stdbool.h>
//单链表数据元素(更改数据元素,修改基本元素结构体和接口的实现即可)
struct item {
//数据项
char no[20];
char name[40];
float price;
bool operator==(const item& a) {
return ( *no== *a.no) && (*name == *a.name) && (price == a.price);
}
};
typedef item Item;
typedef struct Lnode{
Item item;
struct Lnode* next;
}Lnode,*List;
//单链表初始化
bool Listinit(List *L);
//单链表取值
bool GetItem(const List L, int i, Item &e);
//单链表查找
int LocateItem(const List L, Item e);
//单链表插入
bool ListInsert(List *L, int i, Item e);
//单链表删除
bool ListDetele(List* L, Item e);
接口实现
#include<stdio.h>
#include<stdlib.h>
#include"link.h"
//顺序表初始化
bool Listinit(List *L) {
*L = NULL;
return true;
}
//顺序表取值
bool GetItem(const List L, int i, Item &e) {
int j = 1;
List p = L;
while (p && j < i) { //ASL=(n-1)/2 ,即时间复杂度为O(n)
p = p->next;
++j;
}
if (p && (i == j)) {
e = p->item;
return true;
}
else
return false;
}
//顺序表查找
int LocateItem(const List L, Item e) {//ASL为(n+1)/2,则时间复杂度为O(n
int i = 1;
List p = L;
while ( p && !(p->item == e)) {
p = p->next;
++i;
printf("++\n");
}
if (p)
return i;
else
return 0;
}
//顺序表插入
bool ListInsert(List *L, int i, Item e) {
List node = (Lnode*)malloc(sizeof(Lnode));
if (node) {
node->item = e;
node->next = NULL;
}
List p, q;
p = *L; q = *L;
int j = 1;
while (p && j < i) { //ASL=(n-1)/2 ,即时间复杂度为O(n)
q = p;
p = p->next;
++j;
}
if (j > i || i > j) { //i输入错误
fputs("number input error\n", stderr);
return false;
}
else if (i == j) {
if (!q) { //前插结点
if(node)
*L = node;
}
else{ //中插结点 ,后插结点
if (node) {
q->next = node;
node->next = p;
}
}
return true;
}
}
//单链表删除
bool ListDetele(List* L, Item e) {
int LocateItem(const List L, Item e);
int i = -1;
i = LocateItem(*L, e);
if (!i) {
fputs("cannot find\n", stderr);
return false;
}
int j = 1;
List p,q;
p = q = *L;
while (j<i) {
q = p;
p = p->next;
++j;
}
if (!q)
*L = NULL;
else
q->next = p->next;
return true;
}
void close(List* t) {
List p,q;
p = q = *t;
while (q) {
q = p->next;
free(p);
p = q;
}
printf("closed....\n");
}
测试
#include<stdio.h>
#include<stdlib.h>
#include"link.h"
int main(int agrc, char* argv[]) {
extern void close(List * t);
List node;
Listinit(&node);
item e = { "1024","the star",21.22 };
ListInsert(&node, 1, e);
List p = node;
while (p) {
printf("the no : %s\n", p->item.no);
printf("the name : %s\n",p->item.name);
printf("the price: %.2f\n",p->item.price);
p = p->next;
}
ListDetele(&node, e);
if (node)
printf("deleted...\n");
close(&node);
return 0;
}
/*
the no : 1024
the name : the star
the price: 21.22
deleted...
closed....
D:\vs\Data_Struct\Debug\Data_Struct.exe (进程 6788)已退出,代码为 0。
按任意键关闭此窗口. . .
*/
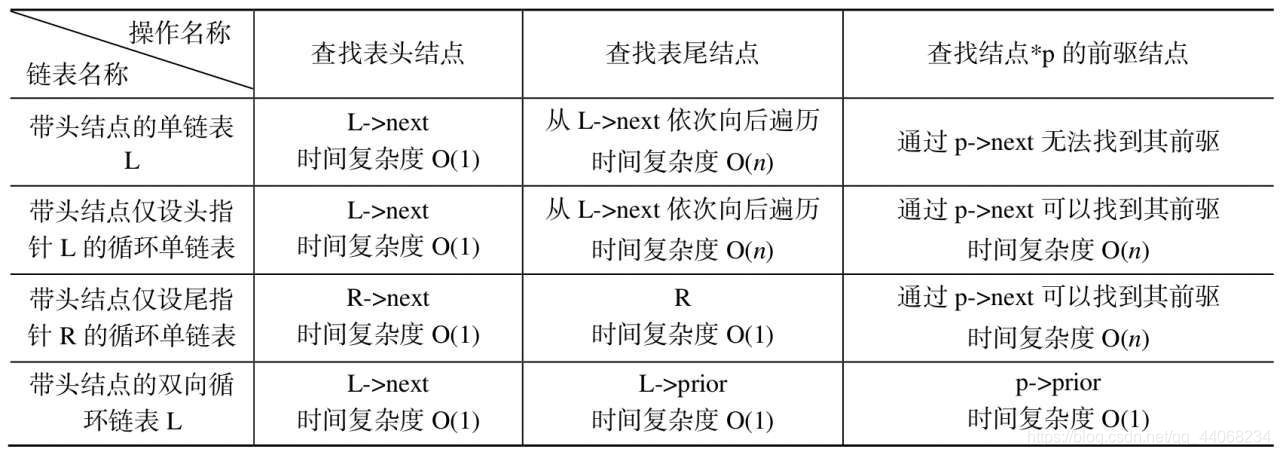
再简单说一下适合线性表的循环链表和双向链表。相较于单链表有各自的适用优势,单基本功能都可以使用单链表实现,只是在时间和空间上的利用率的差别。
循环链表可以从任意结点开始遍历全表。
双向链表双向不循环链表适用查看链表前驱结点
双向循环链表可用任意结点任意方向遍历全表下图是书上的总结
总结
书上总结:两种存储方式的特点和适用方式
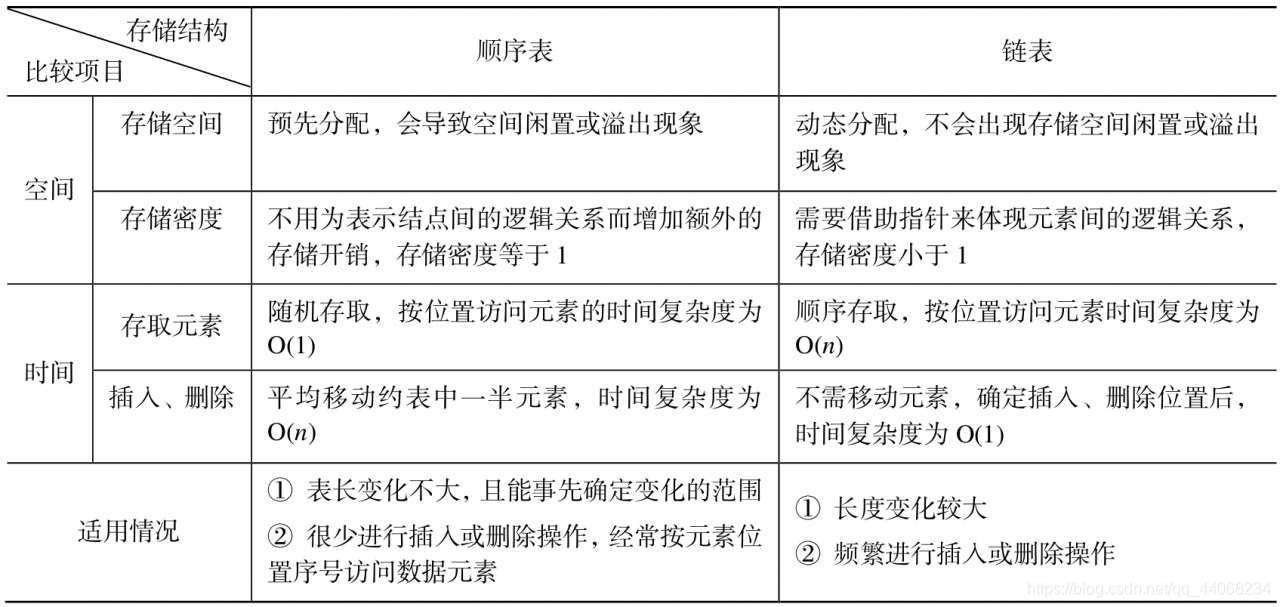








 本文详细介绍了线性表的两种存储结构——顺序存储和链式存储。顺序存储通过连续地址存储线性表元素,实现随机存取,常使用数组表示;链式存储利用结点表示数据元素并存储后续位置信息,适用于动态变化的线性表,文中以单链表为例进行实现。此外,文章还提到了循环链表和双向链表的适用优势。
本文详细介绍了线性表的两种存储结构——顺序存储和链式存储。顺序存储通过连续地址存储线性表元素,实现随机存取,常使用数组表示;链式存储利用结点表示数据元素并存储后续位置信息,适用于动态变化的线性表,文中以单链表为例进行实现。此外,文章还提到了循环链表和双向链表的适用优势。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








