这一节习题数学能力要求比较高,我的有限,如果有不同意见或者我哪里写错了欢迎讨论
练习
1.我们可以更深入地探讨指数族与softmax之间的联系。
(1)计算softmax交叉熵损失l(y,y^)l(\mathbf{y},\hat{\mathbf{y}})l(y,y^)的二阶导数
(2)计算softmax(o)给出的分布⽅差,并与上面计算的⼆阶导数匹配。
解:(1)由公式3.4.9和3.4.10:
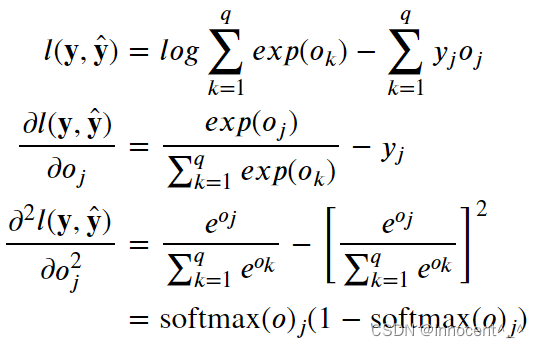
(2)由方差的计算公式,假设o一共有q个,第i个观察对象的softmax计算结果为sis_isi,他们的softmax计算值的平均结果为sˉ\bar ssˉ:
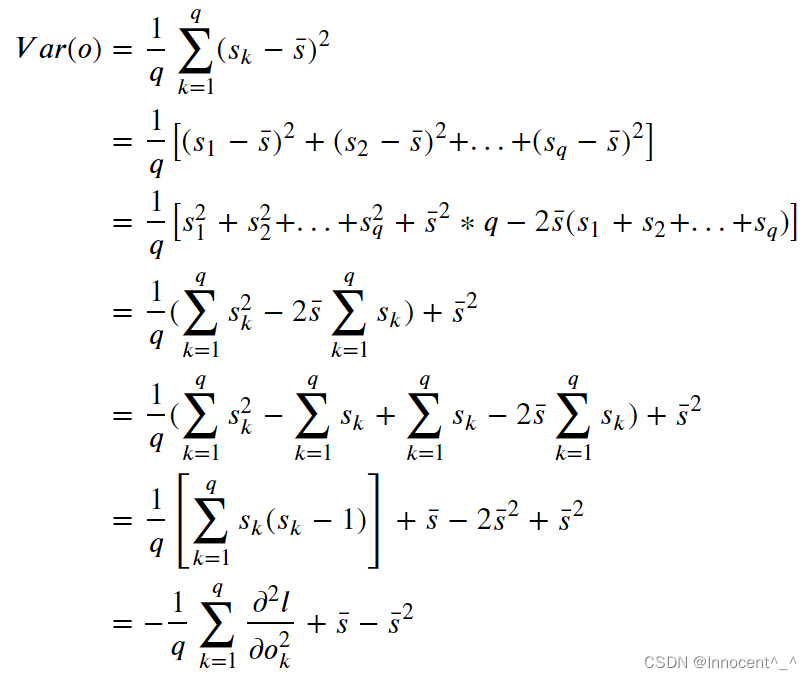
2.假设我们有三个类发⽣的概率相等,即概率向量是(13\frac{1}{3}31,13\frac{1}{3}31,13\frac{1}{3}31)
(1)如果我们尝试为它设计⼆进制代码,有什么问题?
(2)你能设计⼀个更好的代码吗?提示:如果我们尝试编码两个独⽴的观察结果会发⽣什么?如果我们联合编码n个观测值怎么办?
解:(1)有三个类,如果要设置二进制代码至少需要2位。如果采用2位编码,有00、01、10、11四种组合,会出现某一个组合被浪费,而且想构造出题述概率向量非常困难,要根据组合,找新的表达形式,而且需要更改对应的损失函数参数,过程会非常繁琐困难
(2)采用one-hot独热编码。比如分别设置为001、010、100,三位数字中如果某一位是1则说明这个数据样例属于对应的类
3.softmax是对上⾯介绍的映射的误称(虽然深度学习领域中很多⼈都使⽤这个名字)。真正的softmax被定义为RealSoftMax(a, b) = log(exp(a) + exp(b))。
(1)证明:RealSoftMax(a, b) > max(a, b)
假设 a > b:log(ea+eb)>logea=alog(e^a + e^b) > loge^a = alog(ea+eb)>logea=a,反之同理,得证
(2)证明:如果λ>0\lambda > 0λ>0,则λ−1RealSoftMax(λa,λb)>max(a,b)\lambda^{-1}\text{RealSoftMax}(\lambda a, \lambda b) > max(a, b)λ−1RealSoftMax(λa,λb)>max(a,b)
假设 a > b:λ−1log(eλa+eλb)>λ−1logeλa=a\lambda ^{-1}log(e^{\lambda a} + e^{\lambda b}) > \lambda ^{-1}loge^{\lambda a} = aλ−1log(eλa+eλb)>λ−1logeλa=a,反之同理,得证
(3)证明对于λ → ∞,有λ−1\lambda^{-1}λ−1RealSoftMax(λa, λb) → max(a, b)。
直观理解:假设 a > b,λ\lambdaλ→∞则有λa\lambda aλa >> λb\lambda bλb,那么log(eλa+eλb)log(e^{\lambda a} + e^{\lambda b})log(eλa+eλb)中eλbe^{\lambda b}eλb可以忽略不计。
正常做法:使用夹逼定理
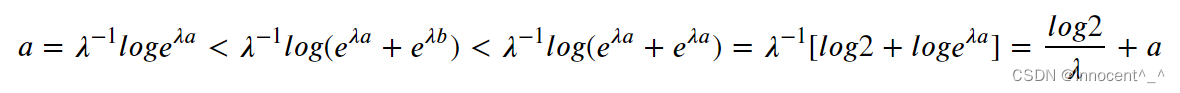
而λ−1log2\lambda ^{-1}log2λ−1log2在λ\lambdaλ趋于无穷时为0,根据夹逼定理得到原式极限为a,反之同理
4.soft-min会是什么样子
解:假设有q个观察结果,那么softmin(o)i=e−i∑k=1q e−k\text{softmin}(o)_i = \frac{e^{-i}}{\sum^{q}_{k=1} \ e^{-k}}softmin(o)i=∑k=1q e−ke−i
5.将其扩展到两个以上的数字。
解:Realsoftmax(a,b,c,…)=log(ea+eb+ec+...e^a + e^b + e^c + ...ea+eb+ec+...)




 本文探讨了深度学习中涉及的一些关键数学概念,包括softmax函数的性质及其应用,通过具体例题解析了softmax函数与指数族的关系,同时讨论了二进制编码在多分类问题中的局限性和改进方案。
本文探讨了深度学习中涉及的一些关键数学概念,包括softmax函数的性质及其应用,通过具体例题解析了softmax函数与指数族的关系,同时讨论了二进制编码在多分类问题中的局限性和改进方案。
















 6813
6813

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








