最大子矩阵和（学习心得+AC代码）

例题：无奈网上没有一篇我能看懂的题解，最后还是请教别人才过了

如果不懂一维的最大子段和，可以先看结尾-》

Description
给出一个m×n的矩阵，请输出它的最大子矩阵和。
Input
多测试用例，每个测试用例：
第一行是两个正整数m和n，表示该矩阵的行数和列数。1 < m, n < 400
接下来m行，每行n个整数，空格分隔。
Output
每个测试用例输出一行：该矩阵的最大子矩阵和。运算结果在int范围内。
Sample Input
4 4
0 -2 -7 0
9 2 -6 2
-4 1 -4 1
-1 8 0 -2
Sample Output
15
先给简洁代码：

#include<bits/stdc++.h>
using namespace std;
int a[401][401];
int f[401]; 
int sum[401][401];
int main(void)
{
	int n,m,i,j,maxz;
	while(~scanf("%d %d",&n,&m))
	{
		maxz=-99999999;//不能是0 
		for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
		scanf("%d",&a[i][j]);
		memset(f,0,sizeof(f));
		memset(sum,0,sizeof(sum));
		for(j=1;j<=m;j++)
		for(i=1;i<=n;i++)
		sum[i][j]=a[i][j],sum[i][j]+=sum[i-1][j];//sum是前缀和为了减少下面求第i行到i+k行的时间复杂度
		for(i=1;i<=n;i++){//子矩阵行数 
			for(int k=1;k<=n;k++){//原矩阵行数
			memset(f,0,sizeof(f));//重新初始化 
				if(i==1)
				{
					for(j=1;j<=m;j++){
						f[j]=max(f[j-1]+a[k][j],a[k][j]);
						maxz=max(maxz,f[j]);
					}
				}
				else
				{
					for(j=1;j<=m&&i+k<=n;j++){//j为开始的行数 
						int s=sum[i+k][j]-sum[k-1][j];//将这一列的数总和
						f[j]=max(f[j-1]+s,s);//转化为一维的最大子段和 
						maxz=max(maxz,f[j]); 
					}
				}
			}
		}
		printf("%d\n",maxz);
	}
	return 0;
}

由于所给数据的“坑”（百试百灵，就是AC不了），还有自己对dp的理解不深。
现在把一直调整的代码拿出来

#include<bits/stdc++.h>
using namespace std;
int a[401][401];
//int f[401][401];
int f[401]; 
int sum[401][401];
//int dp[401][401];
int main(void)
{
	int n,m,i,j,maxz;
	while(~scanf("%d %d",&n,&m))
	{
		maxz=-99999999;//不能是0 
		for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
		scanf("%d",&a[i][j]);
		memset(f,0,sizeof(f));
		//memset(dp,0,sizeof(dp));
		memset(sum,0,sizeof(sum));
		/* 
		//............错..........误..........代码....................
		for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
		sum[i][j]=a[i][j],sum[i][j]+=sum[i-1][j];
		/* 
		for(i=1;i<=n;i++)
		for(j=1;j<=m;j++)
		f[i][j]=max(f[i][j-1]+a[i][j],a[i][j]);
		-->这样只能求出该行的最长以j结尾的最大子段和，对于求最大子矩阵并没有什么卵用 */ 
		/* 
		for(i=1;i<=n;i++){
			for(j=1;j<=m;j++){
			//dp[i][j]=max(dp[i-1][j]+sum[i][j],sum[i][j]);----》sum数组记录的是1~j的和，故此dp数组只能求出从a[i][1]开始的最大子矩阵和，故WA 
			dp[i][j]=max(dp[i-1][j]+sum[i][j],f[i][j]);
			maxz=max(maxz,dp[i][j]);
		    }
		}*/ 
		// ............错..........误..........代码....................
		for(j=1;j<=m;j++)
		for(i=1;i<=n;i++)
		sum[i][j]=a[i][j],sum[i][j]+=sum[i-1][j];
		for(i=1;i<=n;i++){//子矩阵行数 
			for(int k=1;k<=n;k++){//原矩阵行数
			memset(f,0,sizeof(f));//重新初始化 
				if(i==1)
				{
					for(j=1;j<=m;j++){
						f[j]=max(f[j-1]+a[k][j],a[k][j]);
						maxz=max(maxz,f[j]);
					}
				}
				else
				{
					for(j=1;j<=m&&i+k<=n;j++){//j为开始的行数 
						int s=sum[i+k][j]-sum[k-1][j];//将这一列的数总和
						f[j]=max(f[j-1]+s,s);//转化为一维的最大子段和 
						maxz=max(maxz,f[j]); 
					}
				}
			}
		}
		printf("%d\n",maxz);
	}
	return 0;
}

能发现自己的错误，还全靠请教dalao,看来讨论是很重要的。

一维

Description
给出n个整数序列（可能为负数）组成的序列a1, a2, …, an，求该序列形如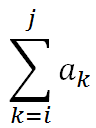的子段和的最大值。当所有整数均为负数时，定义最大子段和为0。
Input
多测试用例。每个测试用例占2行：
第一行是序列的个数n（0 < n ≤ 10000），第二行是n个整数。
Output
为每个测试用例输出一行结果：最大子段和。
Sample Input
6
-2 11 -4 13 -5 -2
3
1 2 3
Sample Output
20
6
dp模板;

#include<bits/stdc++.h>
using namespace std;
int dp[10005];
int a[10005];
int main(void)
{
	int i,n,maxz;
	while(~scanf("%d",&n))
	{
		int flag=0;
		maxz=0;
		memset(dp,0,sizeof(dp));
		for(i=1;i<=n;i++){
			scanf("%d",&a[i]);
			if(a[i])
			flag=1;
		}
		for(int i=1;i<=n;i++){
			dp[i]=max(dp[i-1]+a[i],a[i]);//dp[i]表示以ai结尾的最大子段和 
			maxz=max(dp[i],maxz);
		}
		if(flag==0)
		printf("0\n");
		else
		printf("%d\n",maxz);
	}
}

解释就不解释了，不懂就去看看其他dalao的解释吧，给出代码是为了方便与二维的最大子矩阵和做比较

最后记住一点，一维的最大子段和dp【j】数组是表示以j结尾的最大子段和（就是说不能确定是哪个位置到j的和），所以同理当我们把二维的最大子矩阵和转化为一维的最大子段和时，你要知道子矩阵不是只能从第一行到第i行的子矩阵，也可以是第2，3，4行开始的（k来枚举），所以重点来了：我们转化为一维（f数组）是就要枚举所有行数为1，2，3，4，,i的子矩阵。最后取个max就是答案了

总之：就是把每一列从k行到i行压缩（k<i）为一个值，m个值构成一个一维的数组，对他求最大子段和