基于非线规划算法的船舶能量调度_船舶智能能效优化 csdn-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_43790749/article/details/127021763

本文探讨了在船舶电力系统中，利用非线性规划算法进行能量调度的问题。通过建立详细的电力系统模型，包括发电机、能量存储系统和负载的数学模型，以及相应的约束条件，确保系统的稳定运行和最小化经济成本。实验结果表明，非线性规划算法能有效调整发电机组和ESS出力，适应负载变化，减少燃油消耗并延长ESS寿命，为DRL算法提供了基准和改进方向。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

拟开展能量调度小论文学习分享心得系列文章

前言

在使用深度强化学习算法（Deep Reinforce Learning,DRL）舶能量调度问题中，对智能体调度的结果难以判断，因此需要给出一个基准最优解，使得对智能体的调度结果能做出正确的评价，有助于增强DRL能量调度算法的说服力，同时对DRL能量调度算法的改进具有引导作用。

一、解决方案

系统建模：
首先建立船舶电力系统模型，以发电机组（包括柴油发电机组和燃气轮机发电机组）、能量存储系统(Energy Storage System,ESS)、负载（包括服务负载和推进负载）所构成的全电力船舶（All-Electric Ships,AES）电力系统为研究对象，其示意图如图1所示，其中能量流表示系统能量流向，信息流表示系统内部信息传递以及与能量管理中心之间的通信，即能量管理中心根据负荷变化动态调整各发电机组和ESS出力（出力为负表示充电，为正表示放电），为负载提供功率支撑，下面对各分系统建立能量调度数学模型。
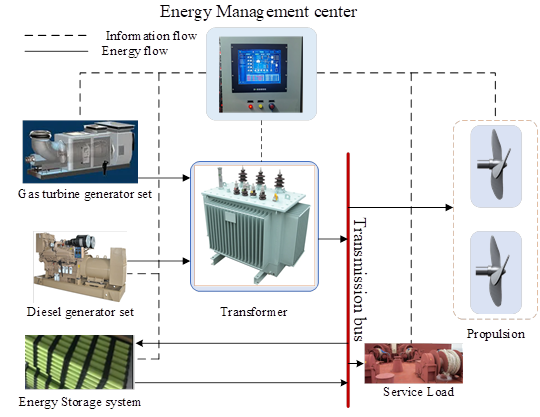在这里插入图片描述图1 AES电力系统拓扑关系图

发电机组建模:
AES发电机组功率应限制在额定功率范围以内，调整功率应限制在最大爬坡功率以内，发电机组功率调整应受式(1)、(2)、(3)和(4)约束，发电机的功率不能大于额定功率。
在这里插入图片描述 (1)
(2)
(3)
(4)
其中 $N$ 表示AES中发电机数， $P_{n}^{rated}$ 表示第 $n$ 台发电机的额定功率， $r_{n}$ 表示第 $n$ 台发电机的最大爬坡率， $P_{n}^{ramp}$ 表示第n台发电机的最大调整功率， $T$ 表示总运行时间， $ΔP_{n,t}$ 表示第 $n$ 台发电机在时刻 $t$ 的调整功率， $Δ t$ 表示时间间隔， $P_{n,t}$ 表示第 $n$ 台发电机在 $t$ 时刻的功率， $P_{n,t-1}$ 表示第 $n$ 台发电机在 $t - 1$ 时刻的功率， $P_{n}^{min}$ 表示第 $n$ 台发电机的最小功率。
发电机燃料消耗（FC）函数可以近似用二阶或三阶的多项式表达。因此，在时刻 $t$ 的燃油消耗成本表示成 $N$ 个发电机的燃料消耗总和，如式（5）所示，其中 $a_{n}$ ， $b_{n}$ ， $c_{n}$ 为多项式系数， $Δ t$ 表示时间间隔。
在这里插入图片描述 (5)
能量存储系统建模:
AES能量存储系统需要受到电量状态(state of Charge,SOC)和出力限制。电池的最大充放电功率不一样，所以需要对其进行区分，并限制其充放电功率大小，否则会造成电池损坏，如式（6）所示；电池的SOC值也需要对其进行限制，放电过程需要限制其最小SOC，如果到达最小SOC值就停止放电，充电过程需要限制其最大SOC，如果到达最大SOC值就停止充电，如式（7）和（8）所示，否则会影响到电池的使用寿命。
在这里插入图片描述 (6)
(7)

在这里插入图片描述 (8)

其中 $P_{ba,c}^{max}$ 表示储能系统充电最大功率， $P_{ba,d}^{max}$ 表示储能系统放电最大功率， $P_{ba,t}$ 表示储能系统在时刻t充放电功率， $P_{ba,t}>0$ 表示ESS放电， $P_{ba,t}<0$ 表示ESS充电，E为储能系统存储的最大能量， $SOC_{min}$ 表示ESS允许的最小电量， $SOC_{max}$ 表示ESS允许的最大电量， $SOC_{t}$ 表示ESS在时刻 $t$ 的荷电状态， $Δ t$ 表示电池充放电时间间隔。
电池在充放电过程中会损耗ESS寿命，可以转化为经济损失来计算，ESS在时刻t的经济损失如式（9）所示。
在这里插入图片描述 (9)
其中 $P_{ba,t}|$ 表示ESS充放电功率的绝对值， $η$ 表示ESS的折旧系数，是一个正常数。
负载建模:
AES上负载包括推进负载和服务负载，服务负载包括空调、雷达、导航设备、照明设备和风机等用电设备，AES总负荷功率如式（10）所示。
在这里插入图片描述 (10)
其中 $P_{Load,t}$ 表示AES总负载， $P_{PL,t}$ 为推进负载， $P_{SE,t}$ 为服务负载。
功率平衡约束:
如果AES电源功率与负载功率不相等，容易造成系统失稳，负载无法正常工作，因此电源和负载功率应保持动态平衡，即发电机组和ESS的功率应该时刻满足负载需求，保证整个电力系统稳定运行，如式（11）所示。
在这里插入图片描述 (11)
从式(11)可以看出ESS在AES电力系统中可作为电源或负载，从而起到一个削峰填谷的作用，可以增强系统的稳定性。当 $P_{ba,t}>0$ ，ESS放电为负提供功率支撑，减少发电机组的压力，当 $P_{ba,t}<0$ ，ESS充电将发电机组多余的功率存储起来为下一步放电做准备。
在AES电力系统环境中，运行成本主要来自于发电机组的燃油消耗和ESS的寿命损耗，那么总经济消耗如式（12)所示。
在这里插入图片描述 (12)

其中 $c_{t}$ 为AES在 $t$ 时刻总经济成本。

二、仿真实验：

以全电力渡轮为研究对象进行实验验证，其中AES包含4个发电机组和一个ESS，实验平台为Ubuntu 20.04，python3.7.5，使用的求解器为Groubi，GPU为1080Ti，CPU为Intel® Core™ i7-8700 CPU @ 3.20GHz × 12。
AES包括两个燃气轮机组（DG1，DG3）、两个柴油机发电机组（DG2，DG4）和一个ESS，其具体参数如表1所示，其经济参数如表2所示。
在这里插入图片描述
图2测试负荷数据
实现代码如下：

import numpy as np
import random
# %% Plot the result
import pandas as pd
import matplotlib.pyplot as plt
import time
import numpy as np
# import scipy.sparse as sp
import gurobipy as gp
from gurobipy import GRB
import matplotlib.pyplot as plt
import matplotlib
from pylab import mpl

# %%
import pulp

def write_data(data,name):
    test = pd.DataFrame(data=data,columns=name)
    test.to_csv('./result/CSV/{}.csv'.format(name[0]))


def dict_to_list(data):
    data_list = []
    for key,value in data.items():
        data_list.append(value)
    return data_list

def train(soc=0.6):

    #电机参数
    # G1价格
    a1_cost = 35.1
    b1_cost = 86.5
    c1_cost = 579
    # G2价格
    a2_cost = 59.3
    b2_cost = 36
    c2_cost = 478
    # G3价格
    a3_cost = 34.1
    b3_cost = 83.6
    c3_cost = 556
    # G4价格
    a4_cost = 57.3
    b4_cost = 30.1
    c4_cost = 497

    #额定功率
    DG1_rated_power = 1.2 * 20
    DG2_rated_power = 0.25 * 20
    DG3_rated_power = 1.3 * 20
    DG4_rated_power = 0.3 * 20

    #爬坡率
    DG1_ramp_power = 0.5 * DG1_rated_power
    DG2_ramp_power = 0.6 * DG2_rated_power
    DG3_ramp_power = 0.55 * DG3_rated_power
    DG4_ramp_power = 0.67 * DG4_rated_power

    P_rated = 0.3 * 20  # pu
    E_rated = 0.9 * 20 # pu  6MW

    C_E = 50000
    LC = 5000
    eta = 1.
    DOD = 1.
    wear_cost = C_E / eta / DOD / LC


    #初始化条件
    init_DG1_power = 0.
    init_DG2_power = 0.  # 这个地方会影响训练嘛
    init_DG3_power = 0.
    init_DG4_power = 0.  #

    init_SOC = soc  # np.round(np.random.uniform(0.2,0.8),1)#0.6  # initial SOC，能否随机一个SOC?
    soc_min = 0.2
    soc_max = 0.8

    #不同时间断面负荷
    load_data = pd.read_csv("data/load_test_50.csv")  # 这个就是负荷数据集
    data = load_data['load'].values
    load_data = data[:48]


    # 创建模型
    m = gp.Model('CM')
    # 创建变量
    power_DG1 = m.addVars(48,vtype=GRB.CONTINUOUS,lb=0,ub=DG1_rated_power,name='powers_DG1')
    delta_power_DG1 = m.addVars(48,vtype=GRB.CONTINUOUS,lb=-DG1_ramp_power,ub=DG1_ramp_power,name='delta_powers_DG1')

    power_DG2 = m.addVars(48, vtype=GRB.CONTINUOUS,lb=0,ub=DG2_rated_power, name='powers_DG2')
    delta_power_DG2 = m.addVars(48, vtype=GRB.CONTINUOUS,lb=-DG2_ramp_power,ub=DG2_ramp_power, name='delta_powers_DG2')

    power_DG3 = m.addVars(48, vtype=GRB.CONTINUOUS, lb=0, ub=DG3_rated_power, name='powers_DG3')
    delta_power_DG3 = m.addVars(48, vtype=GRB.CONTINUOUS, lb=-DG3_ramp_power, ub=DG3_ramp_power,
                                name='delta_powers_DG3')

    power_DG4 = m.addVars(48, vtype=GRB.CONTINUOUS, lb=0, ub=DG4_rated_power, name='powers_DG4')
    delta_power_DG4 = m.addVars(48, vtype=GRB.CONTINUOUS, lb=-DG4_ramp_power, ub=DG4_ramp_power,
                                name='delta_powers_DG4')

    power_battery_abs = m.addVars(48,vtype=GRB.CONTINUOUS,lb=-P_rated,ub=P_rated,name='battery')
    power_battery_y = m.addVars(48,vtype=GRB.CONTINUOUS,lb=-P_rated,ub=P_rated,name='battery_y')
    SOC = m.addVars(48, vtype=GRB.CONTINUOUS, lb=soc_min, ub=soc_max, name='soc')

    #power_battery_dis = m.addVars(48, vtype=GRB.CONTINUOUS, lb=-P_rated,ub=P_rated, name='battery_dis')
    #power_battery_charge = m.addVars(48, vtype=GRB.CONTINUOUS, lb=-P_rated,ub=P_rated, name='battery_charge')


    #dis_bool = m.addVars(48,vtype=GRB.CONTINUOUS,name='dis_Y')
    #dis_1 = m.addVars(48, vtype=GRB.CONTINUOUS,lb=1,ub=1, name='dis_1')
    #dis_0 = m.addVars(48,vtype=GRB.CONTINUOUS,lb=0,ub=0,name='dis_0')


    #cost_steps = m.addVars(48,vtype=GRB.CONTINUOUS,name='cost_steps')

    #设置目标函数
    DG1_cost = gp.quicksum(a1_cost * (power_DG1[i]) ** 2 + b1_cost * (power_DG1[i] ) +
                c1_cost for i in range(48)) / 2.
    DG2_cost = gp.quicksum(a2_cost * (power_DG2[i] ) ** 2 + b2_cost * (power_DG2[i] ) +
                c2_cost for i in range(48)) / 2.
    DG3_cost = gp.quicksum(a3_cost * (power_DG3[i]) ** 2 + b3_cost * (power_DG3[i]) +
                           c3_cost for i in range(48)) / 2.
    DG4_cost = gp.quicksum(a4_cost * (power_DG4[i]) ** 2 + b4_cost * (power_DG4[i]) +
                           c4_cost for i in range(48)) / 2.
    battery_costs = gp.quicksum(wear_cost * power_battery_abs[i] / 2. for i in range(48))
    m.setObjective(DG1_cost + DG2_cost + DG3_cost + DG4_cost+ battery_costs, GRB.MINIMIZE)  # 设置目标函数
    #添加约束
    m.addConstrs((power_battery_abs[i] == gp.abs_(power_battery_y[i]) for i in range(48)),name='battery_abs')
    #m.addConstrs((dis_0[i] == power_battery_y[i] + power_battery_abs[i]  for i in range(48)),name='dis_0')
    #m.addConstrs((dis_1[i] == power_battery_y[i] - power_battery_abs[i] for i in range(48)), name='dis_1')
    #m.addConstrs((dis_1[i]==1 if dis_1[i]==0 else 0 for i in range(48)))
    #m.addConstrs((power_battery_dis[i]==power_battery_y[i] if power_battery_abs[i] == power_battery_y[i] else 0 for i in range(48)),name='battery_dis')
    #m.addConstrs((power_battery_charge[i]==power_battery_y[i] if power_battery_abs[i] == -power_battery_y[i] else 0 for i in range(48)),name='battery_charge')
    m.addConstrs((power_DG1[i] == delta_power_DG1[i] + init_DG1_power if i == 0 else power_DG1[i] == power_DG1[
        i - 1] + delta_power_DG1[i] for i in range(48)), name='DG1_power_computer')
    m.addConstrs((power_DG2[i] == delta_power_DG2[i] + init_DG2_power if i == 0 else power_DG2[i] == power_DG2[
        i - 1] + delta_power_DG2[i] for i in range(48)), name='DG2_power_computer')
    m.addConstrs((power_DG3[i] == delta_power_DG3[i] + init_DG3_power if i == 0 else power_DG3[i] == power_DG3[
        i - 1] + delta_power_DG3[i] for i in range(48)), name='DG3_power_computer')
    m.addConstrs((power_DG4[i] == delta_power_DG4[i] + init_DG4_power if i == 0 else power_DG4[i] == power_DG4[
        i - 1] + delta_power_DG4[i] for i in range(48)), name='DG4_power_computer')
    m.addConstrs((SOC[i] == init_SOC - power_battery_y[i] /E_rated /2 if i == 0 else SOC[i] == SOC[i - 1] - power_battery_y[i] / E_rated /2 for i in range(48)),name='SOC_computer')
    m.addConstrs((power_DG1[i] + power_DG2[i] + power_DG3[i] + power_DG4[i] + power_battery_y[i]==load_data[i] for i in range(48)),name='power_balance')
    #m.addConstrs((cost_steps[i]== a1_cost * (power_DG1[i]) ** 2 + b1_cost * (power_DG1[i]) + c1_cost +
                                  #a2_cost * (power_DG2[i]) ** 2 + b2_cost * (power_DG2[i]) + c2_cost +
                                  #wear_cost * power_battery_abs[i] / 2. for i in range(48)),name='cost')

    #m.addLConstr(init_SOC<=SOC[47])
    #m.addLConstr(SOC[47]<= 2.2*init_SOC)

    # 求解设置 MIPGap越小，求解精度越高，耗时越长。
    m.setParam('MIPGap', 0.000009)  # or m.Params.MIPGap = 0.09

    # 优化求解
    m.optimize()
    print('目标值为：', m.objVal)
    print("---------- 打印各项参数值——————")
    power_DG1 = m.getAttr('x', power_DG1)
    #power_DG1_delta = m.getAttr('x', delta_power_DG1)
    power_DG2 = m.getAttr('x', power_DG2)
    power_DG3 = m.getAttr('x', power_DG3)
    power_DG4 = m.getAttr('x', power_DG4)

    power_DG2_delta = m.getAttr('x',delta_power_DG2)
    power_battery = m.getAttr('x', power_battery_y)
    SOC_battery = m.getAttr('x',SOC)
    print("delta_DG2:",power_DG2_delta)
    print("DG1:",power_DG1)
    print("DG2:",power_DG2)
    print("DG3:", power_DG3)
    print("DG4:", power_DG4)
    print("battery:",power_battery)
    dict_load = {}
    for i, data in enumerate(load_data):
        dict_load[i] = data
    print("Load:", dict_load)
    print("SOC:",SOC_battery)


    DG1_power_list = dict_to_list(power_DG1)
    DG2_power_list = dict_to_list(power_DG2)
    DG3_power_list = dict_to_list(power_DG3)
    DG4_power_list = dict_to_list(power_DG4)

    battery_power_list = dict_to_list(power_battery)
    SOC_list = dict_to_list(SOC_battery)
    load_list = dict_to_list(dict_load)
    costs = [a1_cost * (DG1_power_list[i]) ** 2 + b1_cost * (DG1_power_list[i]) + c1_cost +
             a2_cost * (DG2_power_list[i]) ** 2 + b2_cost * (DG2_power_list[i]) + c2_cost +
             wear_cost * np.abs(battery_power_list[i]) / 2. for i in range(48)]

    action = np.concatenate(
        [np.array(DG1_power_list)[None, :], np.array(DG2_power_list)[None, :],np.array(DG3_power_list)[None, :],\
         np.array(DG4_power_list)[None, :], \
         np.array(battery_power_list)[None, :], np.array(load_list)[None, :], np.array(SOC_list)[None, :] \
            , np.array(costs)[None, :]], axis=0)
    action = action.T
    name = ['DG1', 'DG2','DG3','DG4','Battery', 'Load', 'SOC','Only_Cost']
    action_record = pd.DataFrame(columns=name, data=action)
    action_record.to_csv('./result/CSV/actor_no_LP_{}.csv'.format(init_SOC), encoding='gbk')
if __name__ == '__main__':
    train(soc=0.6)

设置初始SOC0=0.6，测试天的负荷情况如图2所示。以最小化经济性为目标，在上述电力系统模型约束条件下，使用非线性规划算法对进行求解，以Groubi求解器进行求解，最终最小经济为391423$。能量调度结果如图3所示。可以看到，使用非线性规划算法求出的精确解能根据负载变化实时调整各发电机组和ESS出力，实现动态平衡，同时能够根据负载的高低峰进行充放电，算法也充分考虑到了ESS的寿命损耗，因此也尽量控制了ESS合理充放电，最终实现了经济最小化。从SOC变化中也可以看到，ESS在船舶启航阶段，处于负低峰期，ESS进行充电，直到达到最大SOC，为将来的负荷高峰做准备，后面ESS保持不出力状态，避免ESS寿命损耗，在负荷高峰ESS保持持续放电状态直到达到最小SOC以降低发电机组出力，减少燃油消耗，后续进入负荷低峰期后进行小功率充电和放电以保持经济最优。
在这里插入图片描述图3 调度结果