(一)蚁群算法
1.起源
蚁群优化(ant colony optimization, ACO)是20世纪 90年代初由意大利学者 M.Dorigo等通过模拟蚂蚁的 行为而提出的一种随机优化 技术。
最初用于求解旅行商问题, 现在已经成功用于许多组合 Macro Dorigo 优 化 问 题 。 本 节 课 将 介 绍 ACO算法的基本原理和实现 技术,并通过介绍求解旅行 商问题的ACO算法了解实现 细节。
2.原理
蚁群算法的基本思想来源于自然界蚂蚁觅食的最短路径原理,根据昆虫科学家的观察,发现自然界的蚂蚁虽然视觉不发达,但它们可以在没有任何提示的情况下找到从食物源到巢穴的最短路径,并在周围环境发生变化后,自适应地搜索新的最佳路径。
蚂蚁在寻找食物源的时候,能在其走过的路径上释放一种叫信息素的激素,使一定范围内的其他蚂蚁能够察觉到。当一些路径上通过的蚂蚁越来越多时,信息素也就越来越多,蚂蚁们选择这条路径的概率也就越高,结果导致这条路径上的信息素又增多,蚂蚁走这条路的概率又增加,生生不息。这种选择过程被称为蚂蚁的自催化行为。对于单个蚂蚁来说,它并没有要寻找最短路径,只是根据概率选择;对于整个蚁群系统来说,它们却达到了寻找到最优路径的客观上的效果,这就是群体智能。

3.代码实例实现
%% 旅行商问题(TSP)优化
%% 清空环境变量
clear all
clc
%% 导入数据
load matlab1.mat
%% 计算城市间相互距离
fprintf('Computing Distance Matrix... \n');
n = size(citys,1);
D = zeros(n,n);
for i = 1:n
for j = 1:n
if i ~= j
D(i,j) = sqrt(sum((citys(i,:) - citys(j,:)).^2));
else
D(i,j) = 1e-4;
end
end
end
%% 初始化参数
fprintf('Initializing Parameters... \n');
m = 50; % 蚂蚁数量
alpha = 1; % 信息素重要程度因子
beta = 5; % 启发函数重要程度因子
rho = 0.1; % 信息素挥发因子
Q = 1; % 常系数
Eta = 1./D; % 启发函数
Tau = ones(n,n); % 信息素矩阵
Table = zeros(m,n); % 路径记录表
iter = 1; % 迭代次数初值
iter_max = 150; % 最大迭代次数
Route_best = zeros(iter_max,n); % 各代最佳路径
Length_best = zeros(iter_max,1); % 各代最佳路径的长度
Length_ave = zeros(iter_max,1); % 各代路径的平均长度
%% 迭代寻找最佳路径
figure;
while iter <= iter_max
fprintf('迭代第%d次\n',iter);
% 随机产生各个蚂蚁的起点城市
start = zeros(m,1);
for i = 1:m
temp = randperm(n);
start(i) = temp(1);
end
Table(:,1) = start;
% 构建解空间
citys_index = 1:n;
% 逐个蚂蚁路径选择
for i = 1:m
% 逐个城市路径选择
for j = 2:n
tabu = Table(i,1:(j - 1)); % 已访问的城市集合(禁忌表)
allow_index = ~ismember(citys_index,tabu);
allow = citys_index(allow_index); % 待访问的城市集合
P = allow;
% 计算城市间转移概率
for k = 1:length(allow)
P(k) = Tau(tabu(end),allow(k))^alpha * Eta(tabu(end),allow(k))^beta;
end
P = P/sum(P);
% 轮盘赌法选择下一个访问城市
Pc = cumsum(P);
target_index = find(Pc >= rand);
target = allow(target_index(1));
Table(i,j) = target;
end
end
% 计算各个蚂蚁的路径距离
Length = zeros(m,1);
for i = 1:m
Route = Table(i,:);
for j = 1:(n - 1)
Length(i) = Length(i) + D(Route(j),Route(j + 1));
end
Length(i) = Length(i) + D(Route(n),Route(1));
end
% 计算最短路径距离及平均距离
if iter == 1
[min_Length,min_index] = min(Length);
Length_best(iter) = min_Length;
Length_ave(iter) = mean(Length);
Route_best(iter,:) = Table(min_index,:);
else
[min_Length,min_index] = min(Length);
Length_best(iter) = min(Length_best(iter - 1),min_Length);
Length_ave(iter) = mean(Length);
if Length_best(iter) == min_Length
Route_best(iter,:) = Table(min_index,:);
else
Route_best(iter,:) = Route_best((iter-1),:);
end
end
% 更新信息素
Delta_Tau = zeros(n,n);
% 逐个蚂蚁计算
for i = 1:m
% 逐个城市计算
for j = 1:(n - 1)
Delta_Tau(Table(i,j),Table(i,j+1)) = Delta_Tau(Table(i,j),Table(i,j+1)) + Q/Length(i);
end
Delta_Tau(Table(i,n),Table(i,1)) = Delta_Tau(Table(i,n),Table(i,1)) + Q/Length(i);
end
Tau = (1-rho) * Tau + Delta_Tau;
% 迭代次数加1,清空路径记录表
% figure;
%最佳路径的迭代变化过程
[Shortest_Length,index] = min(Length_best(1:iter));
Shortest_Route = Route_best(index,:);
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
pause(0.3);
iter = iter + 1;
Table = zeros(m,n);
% end
end
%% 结果显示
[Shortest_Length,index] = min(Length_best);
Shortest_Route = Route_best(index,:);
disp(['最短距离:' num2str(Shortest_Length)]);
disp(['最短路径:' num2str([Shortest_Route Shortest_Route(1)])]);
%% 绘图
figure(1)
plot([citys(Shortest_Route,1);citys(Shortest_Route(1),1)],...
[citys(Shortest_Route,2);citys(Shortest_Route(1),2)],'o-');
grid on
for i = 1:size(citys,1)
text(citys(i,1),citys(i,2),[' ' num2str(i)]);
end
text(citys(Shortest_Route(1),1),citys(Shortest_Route(1),2),' 起点');
text(citys(Shortest_Route(end),1),citys(Shortest_Route(end),2),' 终点');
xlabel('城市位置横坐标')
ylabel('城市位置纵坐标')
title(['蚁群算法优化路径(最短距离:' num2str(Shortest_Length) ')'])
figure(2)
plot(1:iter_max,Length_best,'b',1:iter_max,Length_ave,'r:')
legend('最短距离','平均距离')
xlabel('迭代次数')
ylabel('距离')
title('各代最短距离与平均距离对比')
(四) 运行结果
优化路径:
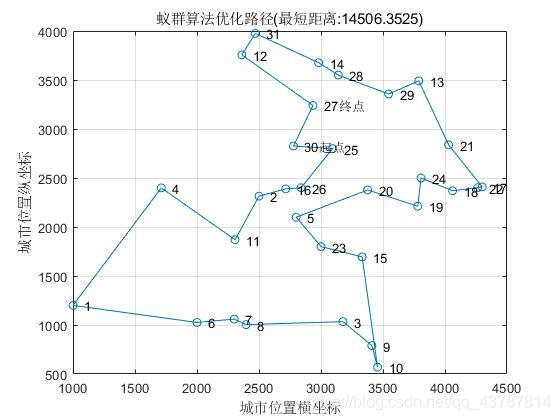
各代最短距离与平均距离对比:
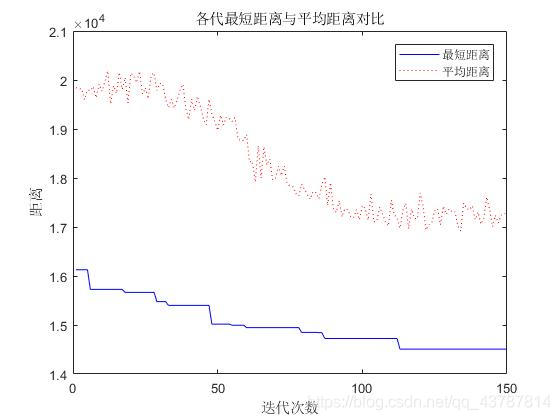
最短距离:14506.3525
最短路径:30 25 26 16 2 11 4 1 6 7 8 3 9 10 15 23 5 20 19 24 18 22 17 21 13 29 28 14 31 12 27 30
改变以下几个参数分析参数:
beta = 5;
rho = 0.1;
当alpha=1时:
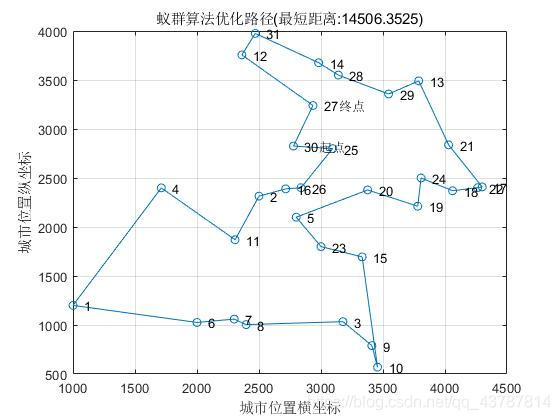

beta = 5;
rho = 0.1;
改变 alpha=5时;


最短距离:14512.2709
最短路径:20 19 24 18 22 17 21 13 29 28 14 31 12 27 30 25 26 16 2 11 4 1 6 7 8 9 10 3 15 23 5 20
beta = 5;
rho = 0.1;
改变 alpha=10时;


最短距离:14600.923
最短路径:5 23 15 3 9 10 8 7 6 1 4 11 2 16 26 20 19 24 18 22 17 21 13 29 28 14 31 12 27 30 25 5
其他参数不变:
alpha=1
rho = 0.1;
beta = 5时;
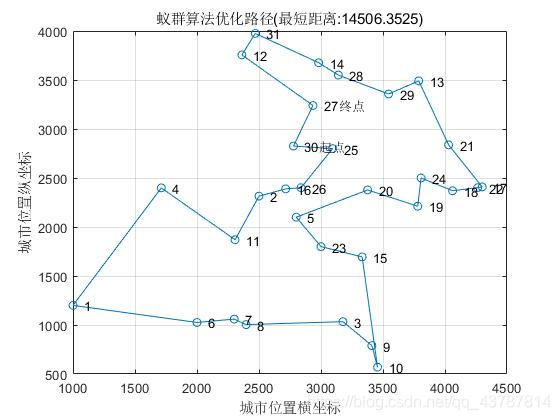
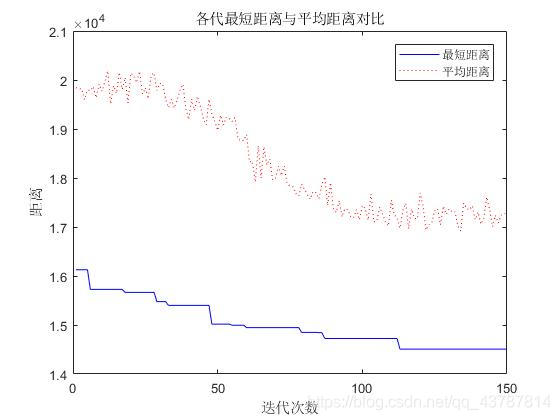
最短距离:14506.3525
最短路径:30 25 26 16 2 11 4 1 6 7 8 3 9 10 15 23 5 20 19 24 18 22 17 21 13 29 28 14 31 12 27 30
alpha=1
rho = 0.1
改变 beta = 10时;


最短距离:14823.8726
最短路径:17 22 18 24 19 20 25 30 26 16 2 11 5 23 15 3 9 10 8 7 6 1 4 12 31 14 28 27 29 13 21 17
alpha=1:
beta = 5;
rho = 2.1时;


最短距离:14785.4806
最短路径:14 28 29 13 21 17 22 18 19 24 20 16 26 5 23 15 10 9 3 8 7 6 1 4 11 2 30 25 27 12 31 14
参数影响分析
m: 蚂蚁数量 。 m数目越多,得到的最优解就越精确,但是会产生不少重复解,随着算法接近最优值的收敛,信息正反馈作用降低,大量的重复工作,消耗了资源,增加了时间复杂度。
alpha :信息素重要程度因子。 alpha值越大,蚂蚁选择之前走过的路径可能性越大,搜索路径的随机性减弱,alpha越小,蚁群搜索范围就会减少,容易陷入局部最优。
beta :启发函数重要程度因子。 beta值越大,蚁群越容易选择局部最优路径,这时算法的收敛速度加快了,但是随机性却不高,容易得到局部的相对最优。
rho :信息素挥发因子。rho过小时,在各路径上残留的信息素过多,导致无效的路径继续被搜索,影响到算法的收敛速度;过大时,无效的路径虽然可以被排除搜索,但是不能保证有效的路径也会被放弃搜索,影响最优值的搜索。
理想参数范围:
alpha:[0,5]
beta:[0,5]
rho:[0.1,0.99]























 2293
2293

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








